Энэ хичээлээр бид талбайг тооцоолж сурах болно хавтгай дүрсүүдгэж нэрлэдэг муруй шугаман трапецууд .

Ийм тоонуудын жишээг доорх зурагт үзүүлэв.

Нэг талаас, тодорхой интеграл ашиглан хавтгай дүрсийн талбайг олох нь маш энгийн зүйл юм. Бид дээрээс нь тодорхой муруйгаар, доороос абсцисса тэнхлэгээр хязгаарлагдсан дүрсийн талбайн тухай ярьж байна ( Үхэр), зүүн ба баруун талд зарим шулуун шугамууд байдаг. Энгийн байдал нь муруй өгсөн функцын тодорхой интеграл нь ийм дүрсийн талбай (муруй шугаман трапец) юм.

Зургийн талбайг тооцоолохын тулд бидэнд хэрэгтэй:

Муруйг тодорхойлох функцийн тодорхой интеграл, энэ нь муруй трапецийг дээрээс нь хязгаарладаг. Эндээс анхны чухал нюанс гарч ирнэ: муруй трапецийг зөвхөн дээрээс төдийгүй доороос нь муруйгаар хязгаарлаж болно. Энэ тохиолдолд яаж ажиллах вэ? Энгийн боловч санах нь чухал: Энэ тохиолдолд интегралыг хасах тэмдгээр авна .

Интеграцийн хязгаарлалт аТэгээд б, зүүн ба баруун талд байгаа дүрсийг хязгаарласан шугамуудын тэгшитгэлээс бид олдог. x = а , x = б, Хаана аТэгээд б- тоо.

Тус тусад нь өөр хэдэн нюансын талаар.

Дээд талын (эсвэл доод) муруй трапецийг хязгаарлах муруй байх ёстой Тасралтгүй ба сөрөг бус функцийн график y = е(x) .

"x" утгууд нь сегментэд хамаарах ёстой [а, б] . Өөрөөр хэлбэл, мөөгний зүслэг гэх мэт мөрүүдийг тооцдоггүй, иш нь энэ сегментэд сайн таарч, малгай нь илүү өргөн байдаг.

Хажуугийн сегментүүд нь цэг болж муудаж болно. Хэрэв та зураг дээр ийм дүрсийг харвал энэ нь таныг төөрөлдүүлэх ёсгүй, учир нь энэ цэг нь "x" тэнхлэг дээр үргэлж үнэ цэнэтэй байдаг. Энэ нь интеграцийн хязгаарт бүх зүйл эмх цэгцтэй байна гэсэн үг юм.

Одоо та томъёо, тооцоолол руу шилжиж болно. Тиймээс талбай смуруй трапецийг томъёогоор тооцоолж болно

Хэрэв е(x) ≤ 0 (функцийн график нь тэнхлэгийн доор байрладаг Үхэр), дараа нь муруй трапецын талбайг томъёог ашиглан тооцоолж болно

Зургийн дээд ба доод хил хоёулаа функц байх тохиолдол байдаг y = е(x) Мөн y = φ (x), дараа нь ийм зургийн талбайг томъёогоор тооцоолно

. (3)

Хамтдаа асуудлыг шийдвэрлэх

Зургийн талбайг (1) томъёогоор тооцоолж болох тохиолдлуудаас эхэлье.

Жишээ 1. Үхэр) ба шулуун x = 1 , x = 3 .

Шийдэл. Учир нь y = 1/xсегмент дээр > 0 байвал муруйн трапецын талбайг (1) томъёогоор олно.

.

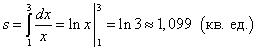Жишээ 2. Функцийн график шугамаар хязгаарлагдсан зургийн талбайг ол x= 1 ба x тэнхлэг ( Үхэр ).

Шийдэл. Томъёо (1)-ийг хэрэглэсний үр дүн:

Хэрэв тэгвэл с= 1/2; хэрэв тэгвэл с= 1/3 гэх мэт.

Жишээ 3. Функцийн график, абсцисса тэнхлэгээр хязгаарлагдсан зургийн талбайг ол. Үхэр) ба шулуун x = 4 .

Шийдэл. Асуудлын нөхцөлд тохирсон зураг нь зүүн сегмент нь цэг болж доройтсон муруй шугаман трапец байна. Интегралын хязгаар нь 0 ба 4 байна. (1) томъёог ашиглан бид муруйн трапецын талбайг олно.

.

Жишээ 4. Зургийн талбайг ол. шугамаар хязгаарлагдана, , болон 1-р улиралд байрладаг.

Шийдэл. Томъёо (1) ашиглахын тулд жишээний нөхцлөөр өгөгдсөн зургийн талбайг гурвалжны талбайн нийлбэр гэж төсөөлье. OABба муруй трапец ABC. Гурвалжны талбайг тооцоолохдоо OABИнтегралын хязгаар нь цэгүүдийн абсцисса юм ОТэгээд А, мөн зургийн хувьд ABC- цэгүүдийн абсцисса АТэгээд C (Ашугамын огтлолцлын цэг юм О.А.ба парабол, ба C- параболын тэнхлэгтэй огтлолцох цэг Үхэр). Шулуун ба параболын тэгшитгэлийг хамтад нь (систем болгон) шийдэж, бид (цэгний абсцисса) олж авна. А) ба (шугам ба параболын огтлолцлын өөр цэгийн абсцисса, энэ нь шийдэлд шаардлагагүй). Үүний нэгэн адил бид , (цэгүүдийн абсцисса) авдаг CТэгээд Д). Одоо бидэнд дүрсний талбайг олоход шаардлагатай бүх зүйл байна. Бид олдог:

Жишээ 5. Муруй трапецын талбайг ол ACDB, хэрэв муруйн тэгшитгэл CDба абсцисса АТэгээд Б 1 ба 2 тус тус.

Шийдэл. Энэхүү муруйн тэгшитгэлийг тоглоомоор илэрхийлцгээе: Муруй шугаман трапецын талбайг (1) томъёогоор олно.

.

Томъёо (2) ашиглан зургийн талбайг тооцоолох тохиолдол руу шилжье.

Жишээ 6. Парабол ба х тэнхлэгээр хязгаарлагдсан дүрсийн талбайг ол. Үхэр ).

Шийдэл. Энэ зураг нь x тэнхлэгийн доор байрладаг. Тиймээс түүний талбайг тооцоолохын тулд бид (2) томъёог ашиглана. Интегралын хязгаар нь абсцисса ба параболын тэнхлэгтэй огтлолцох цэгүүд юм. Үхэр. Тиймээс,

Жишээ 7. Абсцисса тэнхлэгийн хооронд хүрээлэгдсэн талбайг ол ( Үхэр) ба хоёр зэргэлдээ синусын долгион.

Шийдэл. Энэ зургийн талбайг (2) томъёог ашиглан олж болно.

.

Нэр томъёо бүрийг тусад нь олъё:

.

.

Эцэст нь бид талбайг олно:

.

Жишээ 8. Парабол ба муруй хоёрын хооронд байгаа зургийн талбайг ол.

Шийдэл. Тоглоомоор дамжуулан шугамын тэгшитгэлийг илэрхийлье.

Томъёо (2)-ын дагуу талбайг дараах байдлаар авна

,

Хаана аТэгээд б- цэгийн абсцисса АТэгээд Б. Дараах тэгшитгэлийг хамтдаа шийдэж тэдгээрийг олцгооё.

Эцэст нь бид талбайг олно:

Эцэст нь (3) томъёог ашиглан зургийн талбайг тооцоолох тохиолдол гардаг.

Жишээ 9. Параболын хооронд бэхлэгдсэн зургийн талбайг ол Мөн .

2020 оны долдугаар сард НАСА Ангараг гараг руу экспедицээ эхлүүлнэ. Сансрын хөлөгБүртгэгдсэн экспедицийн бүх оролцогчдын нэрс бүхий цахим зөөвөрлөгчийг Ангараг гаригт хүргэх болно.

Хэрэв энэ нийтлэл таны асуудлыг шийдсэн эсвэл танд таалагдсан бол холбоосыг нийгмийн сүлжээн дэх найзуудтайгаа хуваалцаарай.

Эдгээр кодын сонголтуудын аль нэгийг таны вэб хуудасны код руу хуулж, шошгоны хооронд болон шошгоны дараа шууд буулгах шаардлагатай. Эхний хувилбарын дагуу MathJax илүү хурдан ачаалж, хуудсыг бага удаашруулдаг. Гэхдээ хоёр дахь сонголт нь MathJax-ийн хамгийн сүүлийн хувилбаруудыг автоматаар хянаж, ачаалдаг. Хэрэв та эхний кодыг оруулбал үүнийг үе үе шинэчлэх шаардлагатай болно. Хэрэв та хоёр дахь кодыг оруулбал хуудаснууд илүү удаан ачаалах боловч MathJax-ийн шинэчлэлтийг байнга хянах шаардлагагүй болно.

MathJax-г холбох хамгийн хялбар арга бол Blogger эсвэл WordPress дээр: сайтын хяналтын самбарт гуравдагч этгээдийн JavaScript код оруулах зориулалттай виджет нэмж, дээр дурдсан татаж авах кодын эхний эсвэл хоёр дахь хувилбарыг хуулж, виджетийг ойртуулна уу. Загварын эхэнд (дашрамд хэлэхэд, энэ нь огт шаардлагагүй, учир нь MathJax скрипт асинхроноор ачаалагдсан байдаг). Ингээд л болоо. Одоо MathML, LaTeX, ASCIIMathML-ийн тэмдэглэгээний синтаксийг сурснаар та сайтынхаа вэб хуудсанд математикийн томьёо оруулахад бэлэн боллоо.

Ахиад л шинэ жилийн үдэш... хүйтэн жавартай цаг агаар, цонхны шилэн дээр цасан ширхгүүд... Энэ бүхэн намайг... фракталуудын тухай, мөн Вольфрам Альфа энэ талаар мэддэг зүйлийн талаар дахин бичихэд хүргэв. Энэ сэдвээр хоёр хэмжээст фрактал бүтцийн жишээг агуулсан сонирхолтой нийтлэл байна. Энд бид илүү дэлгэрэнгүй авч үзэх болно нарийн төвөгтэй жишээнүүдгурван хэмжээст фракталууд.

Фракталыг геометрийн дүрс эсвэл бие (хоёулаа багц, энэ тохиолдолд цэгүүдийн багц гэсэн үг) хэлбэрээр дүрсэлж (тодорхойлж) болно, тэдгээрийн дэлгэрэнгүй мэдээлэл нь анхны дүрстэй ижил хэлбэртэй байна. Өөрөөр хэлбэл, энэ нь өөрөө ижил төстэй бүтэц бөгөөд нарийн ширийнийг нь судалж үзэхэд бид томруулдаггүй хэлбэрийг харах болно. Харин энгийн тохиолдолд геометрийн дүрс(фрактал биш) томруулж үзэхэд бид илүү ихийг агуулсан дэлгэрэнгүй мэдээллийг харах болно энгийн хэлбэранхны дүрсээс өөрөөсөө илүү. Жишээлбэл, хангалттай томруулсан үед эллипсийн нэг хэсэг нь шулуун шугамын сегмент шиг харагдана. Фракталд ийм зүйл тохиолддоггүй: тэдгээрийн хэмжээ нэмэгдэх тусам бид ижил төвөгтэй хэлбэрийг дахин харах болно, энэ нь өсөлт бүрээр дахин дахин давтагдах болно.

Фракталын шинжлэх ухааныг үндэслэгч Бенуа Манделброт Фрактал ба Шинжлэх ухааны нэрийн урлаг гэсэн өгүүлэлдээ: “Фракталууд нь нарийн ширийн зүйлсийнхээ адил нарийн төвөгтэй геометрийн хэлбэрүүд юм. ерөнхий хэлбэр. Өөрөөр хэлбэл, хэрэв фракталын нэг хэсгийг бүхэлд нь томруулсан бол энэ нь бүхэлдээ, яг эсвэл бага зэрэг гажигтай харагдах болно."

Хэрэглээний асуудлыг шийдвэрлэхэд интеграл ашиглах

Талбайн тооцоо

Үргэлжилсэн сөрөг бус функцийн тодорхой интеграл f(x) нь y = f(x) муруй, O x тэнхлэг ба x = a ба x шулуун шугамаар хязгаарлагдсан муруйн трапецын талбайтай тоон хувьд тэнцүү байна. = б. Үүний дагуу талбайн томъёог дараах байдлаар бичнэ.

Онгоцны дүрсүүдийн талбайг тооцоолох зарим жишээг авч үзье.

Даалгавар No 1. y = x 2 +1, y = 0, x = 0, x = 2 шугамаар хүрээлэгдсэн талбайг тооцоол.

Шийдэл.Талбайг нь тооцоолох ёстой дүрсийг бүтээцгээе.

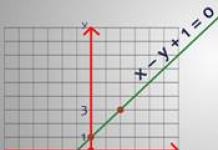
y = x 2 + 1 нь салбарууд нь дээшээ чиглэсэн парабол бөгөөд парабол нь O y тэнхлэгтэй харьцуулахад нэг нэгжээр дээш шилжсэн (Зураг 1).

Зураг 1. y = x 2 + 1 функцийн график

Даалгавар No 2. 0-ээс 1 хүртэлх зайд y = x 2 – 1, y = 0 шугамаар хүрээлэгдсэн талбайг тооцоол.

Шийдэл.Энэ функцийн график нь дээшээ чиглэсэн салбаруудын парабол бөгөөд парабол нь O y тэнхлэгтэй харьцуулахад нэг нэгжээр доошоо шилждэг (Зураг 2).

Зураг 2. y = x 2 – 1 функцийн график

Даалгавар №3. Зургийг зурж, шугамаар хязгаарлагдсан зургийн талбайг тооцоол

y = 8 + 2x – x 2 ба y = 2x – 4.

Шийдэл.Эдгээр хоёр шугамын эхнийх нь х 2-ийн коэффициент сөрөг тул салбарууд нь доош чиглэсэн парабол, хоёр дахь шугам нь хоёр координатын тэнхлэгийг огтолж буй шулуун шугам юм.

Параболыг байгуулахын тулд түүний оройн координатыг олно: y’=2 – 2x; 2 – 2x = 0, x = 1 – оройн абсцисс; y(1) = 8 + 2∙1 – 1 2 = 9 нь түүний ординат, N(1;9) нь орой юм.

Одоо тэгшитгэлийн системийг шийдэж парабол ба шулуун шугамын огтлолцлын цэгүүдийг олцгооё.

Зүүн тал нь тэнцүү тэгшитгэлийн баруун талыг тэгшитгэх.

Бид 8 + 2x – x 2 = 2x – 4 эсвэл x 2 – 12 = 0-ийг авна. .

Тиймээс цэгүүд нь парабол ба шулуун шугамын огтлолцох цэгүүд юм (Зураг 1).

Зураг 3 y = 8 + 2x – x 2 ба y = 2x – 4 функцын графикууд

y = 2x – 4 шулуун шугамыг байгуулъя. Энэ нь координатын тэнхлэгүүдийн (0;-4), (2;0) цэгүүдийг дайран өнгөрнө.

Парабол барихын тулд та түүний 0x тэнхлэгтэй огтлолцох цэгүүдийг ашиглаж болно, өөрөөр хэлбэл 8 + 2x – x 2 = 0 эсвэл x 2 – 2x – 8 = 0 тэгшитгэлийн язгуурыг ашиглаж болно. Виетийн теоремыг ашиглах нь амархан. түүний үндсийг олохын тулд: x 1 = 2, x 2 = 4.

Зураг 3-т эдгээр шугамаар хязгаарлагдсан дүрсийг (параболик сегмент M 1 N M 2) үзүүлэв.

Асуудлын хоёр дахь хэсэг бол энэ зургийн талбайг олох явдал юм. Түүний талбайг томъёоны дагуу тодорхой интеграл ашиглан олж болно .

-тай холбоотой энэ нөхцөл, бид интегралыг авна:

2 Эргэлтийн биеийн эзэлхүүний тооцоо

O x тэнхлэгийг тойрон y = f(x) муруйг эргүүлснээр олж авсан биеийн эзэлхүүнийг дараах томъёогоор тооцоолно.

O y тэнхлэгийг тойрон эргэх үед томъёо нь дараах байдалтай байна.

Даалгавар No4. O x тэнхлэгийн эргэн тойронд x = 0 x = 3 шулуун ба y = муруйн шугамаар хүрээлэгдсэн муруй трапецын эргэлтээс олж авсан биеийн эзэлхүүнийг тодорхойл.

Шийдэл.Зураг зурцгаая (Зураг 4).

Зураг 4. y = функцийн график

Шаардлагатай хэмжээ нь

Даалгавар №5. O y тэнхлэгийг тойрон y = x 2 муруй ба y = 0, y = 4 шулуун шугамаар хязгаарлагдсан муруй трапецын эргэлтээс олж авсан биеийн эзэлхүүнийг тооцоол.

Шийдэл.Бидэнд:

Хяналтын асуултууд

Ox тэнхлэг, y=f(x) муруй ба x=a ба x=b гэсэн хоёр шулуун шугамаар хязгаарлагдсан муруй трапецийг авч үзье (Зураг 85). x-ийн дурын утгыг авъя (зөвхөн a биш, b биш). Үүнд h = dx өсөлтийг өгч, авч үзэж буй муруйд хамаарах AB ба CD шулуун шугам, Ox тэнхлэг, BD нумаар хязгаарлагдсан туузыг авч үзье. Бид энэ зурвасыг энгийн зурвас гэж нэрлэх болно. Энгийн зурвасын талбай нь ACQB тэгш өнцөгтийн талбайгаас BQD муруйн гурвалжны талбайгаас ялгаатай бөгөөд сүүлчийнх нь талбайгаар ялгаатай байдаг. талбай багатэгш өнцөгт BQDM талуудтай BQ = =h=dx) QD=Ay ба талбай нь hAy = Ay dx. h тал багасах тусам Du тал мөн буурч, h-тэй зэрэгцэн тэглэх хандлагатай байна. Тиймээс BQDM-ийн талбай нь хоёр дахь эрэмбийн хязгааргүй жижиг юм. Энгийн зурвасын талбай нь талбайн өсөлт бөгөөд AB-AC ==/(x) dx>-тэй тэнцүү ACQB тэгш өнцөгтийн талбай нь талбайн дифференциал юм. Үүний үр дүнд бид дифференциалыг нэгтгэх замаар тухайн талбайг өөрөө олдог. Харгалзан үзэж буй зургийн хүрээнд l: бие даасан хувьсагч a-аас b болж өөрчлөгдөх тул шаардлагатай талбай 5 нь 5= \f(x) dx-тэй тэнцүү байх болно. (I) Жишээ 1. y - 1 -x* парабол, X =--Fj-, x = 1 шулуун шугамууд ба О* тэнхлэгээр хязгаарлагдсан талбайг тооцоолъё (Зураг 86). Зураг дээр. 87. Зураг. 86. 1 Энд f(x) = 1 - l?, интегралын хязгаар нь a = - ба £ = 1 тул J [*-t]\- -fl -- Г -1-±Л_ 1V1 -l-l- Ii-^ 3) |_ 2 3V 2 / J 3 24 24* Жишээ 2. Синусоид y = sinXy, Ox тэнхлэг ба шулуун шугамаар хязгаарлагдсан талбайг тооцоолъё (Зураг 87). (I) томьёог ашигласнаар A 2 S= J sinxdx= [-cos x]Q =0 -(-1) = lf Жишээ 3. Хаалттай ^у = sin jc синусоидын нумаар хязгаарлагдсан талбайг тооцоол. Ox тэнхлэгтэй зэргэлдээх хоёр огтлолцлын цэгийн хооронд (жишээлбэл, эх ба абсцисса i цэгийн хооронд). Геометрийн үүднээс авч үзвэл энэ талбай нь өмнөх жишээний талбайгаас хоёр дахин их байх болно гэдгийг анхаарна уу. Гэсэн хэдий ч тооцоогоо хийцгээе: I 5= | s\nxdx= [ - cosх)* - - cos i-(-cos 0)= 1 + 1 = 2. o Үнэхээр бидний таамаг зөв болсон. Жишээ 4. Синусоид ба Үхрийн тэнхлэгээр хязгаарлагдсан талбайг нэг үе дээр тооцоол (Зураг 88). Урьдчилсан тооцоогоор энэ талбай нь жишээ 2-оос дөрөв дахин их байх болно. Гэхдээ тооцооллыг хийсний дараа бид “i Г,*i S - \ sin x dx = [ - cos x]0 = = - cos 2l - (-cos 0) = - 1 + 1 = 0. Энэ үр дүнг тодруулах шаардлагатай. Асуудлын мөн чанарыг тодруулахын тулд бид мөн ижил синусоид y = sin l: болон Ox тэнхлэгээр l-ээс 2i хүртэлх мужид хязгаарлагдсан талбайг тооцоолно. (I) томъёог хэрэглэснээр бид 2l $2l sin xdx=[ - cosх]l = -cos 2i~)-c05i=- 1-1 =-2 болно. Тиймээс энэ газар сөрөг талтай болсон гэж бид харж байна. Үүнийг 3-р дасгалд тооцсон талбайтай харьцуулж үзвэл тэдний үнэмлэхүй утгуудижил боловч шинж тэмдгүүд нь өөр өөр байдаг. Хэрэв бид V өмчийг хэрэглэвэл (XI бүлэг, § 4-ийг үзнэ үү) бид 2l I 2l J sin xdx= J sin * dx [ sin x dx = 2 + (- 2) = 0 Энэ жишээнд тохиолдсон зүйл санамсаргүй биш болно. Бие даасан хувьсагч зүүнээс баруун тийш өөрчлөгдөх тохиолдолд Үхрийн тэнхлэгийн доор байрлах талбайг үргэлж интеграл ашиглан тооцоолно. Энэ сургалтанд бид үргэлж тэмдэггүй газруудыг авч үзэх болно. Тиймээс, сая ярилцсан жишээн дээрх хариулт нь: шаардлагатай талбай нь 2 + |-2| байна = 4. Жишээ 5. Зурагт үзүүлсэн BAB-ийн талбайг тооцоолъё. 89. Энэ талбай нь Үхрийн тэнхлэг, y = - xr парабол ба y - = -x+\ шулуун шугамаар хязгаарлагдана. Муруй шугаман трапецын талбай OAB шаардлагатай талбай нь OAM ба MAV гэсэн хоёр хэсгээс бүрдэнэ. А цэг нь парабол ба шулуун шугамын огтлолцох цэг тул 3 2 Y = mx тэгшитгэлийн системийг шийдэж координатыг нь олно. (бид зөвхөн А цэгийн абсциссыг олох хэрэгтэй). Системийг шийдэж, бид l-ийг олно; = ~. Тиймээс талбайг хэсэгчлэн, эхний квадратаар тооцоолох хэрэгтэй. OAM, дараа нь pl. MAV: .... G 3 2, 3 G xP 3 1/2 U 2. QAM-^x)