I denne leksjonen skal vi lære å regne arealet av flate figurer som kalles buede trapeser .

Eksempler på slike former er vist i figuren nedenfor.

På den ene siden er det ekstremt enkelt å finne arealet til en flat figur ved å bruke en bestemt integral. Vi snakker om området til en figur, som er begrenset ovenfra av en viss kurve, nedenfra - av abscisseaksen ( Okse), og noen rette linjer til venstre og høyre. Enkelheten er det det bestemte integralet til funksjonen som kurven er gitt til er arealet til en slik figur(buet trapes).

For å beregne arealet av figuren trenger vi:

1. Det bestemte integralet til funksjonen som definerer kurven , som begrenser den buede trapesen ovenfra. Og her oppstår den første betydelige nyansen: en buet trapes kan begrenses av en kurve ikke bare ovenfra, men også nedenfra ... Hvordan gå frem i dette tilfellet? Enkelt, men viktig å huske: integralet i dette tilfellet er tatt med et minustegn .
2. Integrasjonsgrenser en og b, som vi finner fra ligningene til linjene som binder figuren til venstre og høyre: x = en , x = b, hvor en og b- tall.

Hver for seg, om noen flere nyanser.

Kurven som avgrenser den buede trapesen over (eller under) må være grafen til en kontinuerlig og ikke-negativ funksjon y = f(x) .

X-verdier må tilhøre linjesegmentet [en, b]. Det vil si at det for eksempel ikke tas hensyn til linjer som et kutt av en sopp, der benet passer godt inn i dette segmentet, og hetten er mye bredere.

Sidesegmenter kan degenerere til punkter ... Hvis du ser en slik figur på tegningen, bør dette ikke forvirre deg, siden dette punktet alltid har sin egen verdi på x-aksen. Det betyr at alt er i orden med grensene for integrering.

Nå kan du gå videre til formler og beregninger. Altså området s krumlinjet trapes kan beregnes med formelen

Hvis f(x) ≤ 0 (grafen til funksjonen er plassert under aksen Okse), deretter buet trapesformet område kan beregnes med formelen

Det er også tilfeller når både øvre og nedre grenser til figuren er henholdsvis funksjoner. y = f(x) og y = φ (x) , så beregnes arealet til en slik figur ved hjelp av formelen

. (3)

Vi løser problemer sammen

La oss starte med tilfellene når arealet av figuren kan beregnes ved hjelp av formelen (1).

Eksempel 1.Okse) og rette linjer x = 1 , x = 3 .

Løsning. Fordi y = 1/x> 0 på segmentet, så er arealet av den krumlinjede trapesen funnet av formelen (1):

.

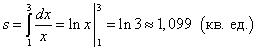Eksempel 2. Finn arealet til en figur avgrenset av grafen til en funksjon, en rett linje x= 1 og abscissen ( Okse ).

Løsning. Resultatet av å bruke formel (1):

Hvis da s= 1/2; hvis da s= 1/3 osv.

Eksempel 3. Finn arealet av figuren avgrenset av grafen til funksjonen, abscisseaksen ( Okse) og direkte x = 4 .

Løsning. Figuren som tilsvarer tilstanden til problemet er en krumlinjet trapes, der venstre segment har degenerert til et punkt. Grensene for integrasjon er 0 og 4. Siden, i henhold til formel (1), finner vi arealet til en krumlinjet trapes:

.

Eksempel 4. Finn arealet av figuren avgrenset av linjene og plassert i 1. kvartal.

Løsning. For å bruke formel (1), representerer vi arealet av figuren gitt av betingelsene i eksemplet som summen av arealene til trekanten OAB og buet trapes ABC... Når du beregner arealet til en trekant OAB grensene for integrering er abscissen av punktene O og EN, og for figuren ABC- abscisse av poeng EN og C (EN er skjæringspunktet mellom linjen OA og parabler, og C- skjæringspunktet mellom parabelen og aksen Okse). Ved å løse sammen (som et system) likningene til en rett linje og en parabel, får vi (abscissen til punktet EN) og (abscissen til et annet skjæringspunkt mellom den rette linjen og parabelen, som ikke er nødvendig for løsningen). På samme måte får vi, (abscisses av poeng C og D). Nå har vi alt for å finne arealet av figuren. Vi finner:

Eksempel 5. Finn arealet til en buet trapes ACDB hvis ligningen til kurven CD og abscisser EN og B henholdsvis 1 og 2.

Løsning. La oss uttrykke denne ligningen av kurven i form av spillet: Arealet til den buede trapesen er funnet av formelen (1):

.

Vi vender oss til tilfellene når arealet av figuren kan beregnes med formelen (2).

Eksempel 6. Finn arealet til en figur avgrenset av en parabel og abscisseaksen ( Okse ).

Løsning. Denne figuren er plassert under abscisseaksen. Derfor, for å beregne arealet, vil vi bruke formel (2). Grensene for integrering er abscissen og skjæringspunktene mellom parablen og aksen Okse... Derfor,

Eksempel 7. Finn området innelukket mellom abscisseaksen ( Okse) og to tilstøtende sinusbølger.

Løsning. Arealet til denne figuren kan bli funnet med formelen (2):

.

La oss finne hvert begrep separat:

.

.

Til slutt finner vi området:

.

Eksempel 8. Finn arealet av figuren som er innelukket mellom parabelen og kurven.

Løsning. La oss uttrykke ligningene til linjene i form av spillet:

Arealet i henhold til formelen (2) oppnås som

,

hvor en og b- abscisse av poeng EN og B... Vi finner dem ved å løse likningene sammen:

Til slutt finner vi området:

Og til slutt, tilfellene når arealet av figuren kan beregnes ved hjelp av formelen (3).

Eksempel 9. Finn arealet til en figur innelukket mellom parabler og .

NASA vil starte en ekspedisjon til Mars i juli 2020. Romfartøyet vil levere til Mars en elektronisk bærer med navnene på alle registrerte medlemmer av ekspedisjonen.

Hvis dette innlegget løste problemet ditt eller du bare likte det, del lenken til det med vennene dine på sosiale nettverk.

En av disse kodevariantene må kopieres og limes inn i koden til nettsiden din, helst mellom taggene og eller rett etter taggen ... I henhold til det første alternativet laster MathJax raskere og bremser siden mindre. Men det andre alternativet sporer og laster automatisk de nyeste versjonene av MathJax. Hvis du setter inn den første koden, må den oppdateres med jevne mellomrom. Hvis du setter inn den andre koden, vil sidene lastes saktere, men du trenger ikke å overvåke MathJax-oppdateringer konstant.

Den enkleste måten å koble MathJax på er i Blogger eller WordPress: i dashbordet på nettstedet ditt, legg til en widget som er utformet for å sette inn tredjeparts JavaScript-kode, kopier den første eller andre versjonen av lastekoden presentert ovenfor inn i den, og plasser widgeten nærmere begynnelsen av malen (forresten, dette er ikke nødvendig i det hele tatt fordi MathJax-skriptet lastes asynkront). Det er alt. Lær nå MathML-, LaTeX- og ASCIIMathML-markeringssyntaksen, og du er klar til å bygge inn matematiske formler på nettstedets nettsider.

Nok en nyttårsaften ... frostvær og snøflak på vindusruten ... Alt dette fikk meg til å skrive igjen om ... fraktaler, og hva Wolfram Alpha vet om det. Det er en interessant artikkel om dette, som inneholder eksempler på todimensjonale fraktale strukturer. Her skal vi se på mer komplekse eksempler på 3D-fraktaler.

En fraktal kan visualiseres (beskrives) som en geometrisk figur eller kropp (som betyr at begge er et sett, i dette tilfellet et sett med punkter), hvis detaljer har samme form som selve den opprinnelige figuren. Det vil si at det er en selvlignende struktur, med tanke på detaljene som med forstørrelse vil vi se samme form som uten forstørrelse. Mens i tilfellet med en vanlig geometrisk form (ikke en fraktal), når vi zoomer inn, vil vi se detaljer som har en enklere form enn selve originalformen. For eksempel, ved høy nok forstørrelse ser en del av ellipsen ut som et linjestykke. Dette skjer ikke med fraktaler: ved enhver økning vil vi igjen se den samme komplekse formen, som vil gjenta seg om og om igjen med hver økning.

Benoit Mandelbrot, grunnleggeren av vitenskapen om fraktaler, skrev i sin artikkel Fractals and Art for Science: «Fractals er geometriske former som er like komplekse i detaljene som i deres generelle form. En del av fraktalen vil bli forstørret til størrelsen på helheten vil den se ut som en helhet, eller nøyaktig, eller kanskje med en liten deformasjon."

Integrert applikasjon til løsning av anvendte problemer

Beregner areal

Det bestemte integralet til en kontinuerlig ikke-negativ funksjon f (x) er numerisk lik arealet til den buede trapesen avgrenset av kurven y = f (x), aksen O x og rette linjer x = a og x = b. Følgelig er arealformelen skrevet som følger:

La oss se på noen eksempler for å beregne arealene til flate figurer.

Oppgave nr. 1. Regn ut arealet avgrenset av linjene y = x 2 +1, y = 0, x = 0, x = 2.

Løsning. La oss bygge en figur, arealet som vi må beregne.

y = x 2 + 1 er en parabel hvis grener er rettet oppover, og parablen er forskjøvet i forhold til O y-aksen oppover med én enhet (Figur 1).

Figur 1. Graf over funksjonen y = x 2 + 1

Oppgave nummer 2. Regn ut arealet avgrenset av linjene y = x 2 - 1, y = 0 i området fra 0 til 1.

Løsning. Grafen til denne funksjonen er parabelen til grenen, som er rettet oppover, og parablen er forskjøvet i forhold til O y-aksen nedover med én enhet (Figur 2).

Figur 2. Graf over funksjonen y = x 2 - 1

Oppgave nummer 3. Lag en tegning og beregn arealet av figuren avgrenset av linjer

y = 8 + 2x - x 2 og y = 2x - 4.

Løsning. Den første av disse to linjene er en parabel med grener rettet nedover, siden koeffisienten ved x 2 er negativ, og den andre linjen er en rett linje som skjærer begge koordinataksene.

For å bygge en parabel finner vi koordinatene til toppunktet: y ’= 2 - 2x; 2 - 2x = 0, x = 1 - abscissen til toppunktet; y (1) = 8 + 2 ∙ 1 - 1 2 = 9 er ordinaten, N (1; 9) er toppunktet.

Nå vil vi finne skjæringspunktene mellom parabelen og den rette linjen ved å løse ligningssystemet:

Sette likhetstegn mellom høyresidene av ligningen, hvis venstre sider er like.

Vi får 8 + 2x - x 2 = 2x - 4 eller x 2 - 12 = 0, hvorfra .

Så punktene er skjæringspunktene til parabelen og den rette linjen (Figur 1).

Figur 3 Grafer over funksjonene y = 8 + 2x - x 2 og y = 2x - 4

La oss konstruere en rett linje y = 2x - 4. Den går gjennom punktene (0; -4), (2; 0) på koordinataksene.

For å konstruere en parabel kan du også ha dens skjæringspunkter med 0x-aksen, det vil si røttene til ligningen 8 + 2x - x 2 = 0 eller x 2 - 2x - 8 = 0. Ved Vietas teorem er det enkelt for å finne røttene: x 1 = 2, x 2 = 4.

Figur 3 viser en figur (parabolsk segment M 1 N M 2), begrenset av disse linjene.

Den andre delen av oppgaven er å finne arealet til denne figuren. Området kan bli funnet ved å bruke en bestemt integral med formelen .

Med hensyn til denne tilstanden får vi integralen:

2 Beregning av volumet til et omdreiningslegeme

Volumet av legemet oppnådd fra rotasjonen av kurven y = f (x) rundt O x-aksen beregnes med formelen:

Når du roterer rundt O y-aksen, ser formelen slik ut:

Oppgave nummer 4. Bestem volumet av legemet oppnådd fra rotasjonen av en buet trapes avgrenset av rette linjer x = 0 x = 3 og en kurve y = rundt O x-aksen.

Løsning. La oss bygge et bilde (Figur 4).

Figur 4. Graf over funksjonen y =

Det nødvendige volumet er

Oppgave nummer 5. Beregn volumet av legemet oppnådd fra rotasjonen av en buet trapes avgrenset av kurven y = x 2 og rette linjer y = 0 og y = 4 rundt O y-aksen.

Løsning. Vi har:

Gjennomgå spørsmål

Betrakt en buet trapes avgrenset av okseaksen, kurven y = f (x) og to rette linjer: x = a og x = b (fig. 85). La oss ta en vilkårlig verdi av x (men ikke a og ikke b). La oss gi det et inkrement h = dx og vurdere en stripe avgrenset av rette linjer AB og CD, okseaksen og buen BD som tilhører kurven under vurdering. Denne stripen vil bli kalt en elementær stripe. Arealet til en elementær stripe skiller seg fra arealet til rektangelet ACQB med en buet trekant BQD, og ​​arealet til sistnevnte er mindre enn arealet av rektangelet BQDM med sidene BQ = h = dx ) QD = Ay og et areal lik hAy = Ay dx. Med avtagende side h, reduseres også siden Du, og samtidig med h tenderer den til null. Derfor er arealet til BQDM andreordens uendelig liten. Arealet til en elementær stripe er økningen av arealet, og arealet av rektangelet ACQB lik AB-AC == / (x) dx> er arealdifferensialen. Derfor finner vi selve området ved å integrere dets differensial. Innenfor den betraktede figuren varierer den uavhengige variabelen l: fra a til b, så det nødvendige arealet 5 vil være lik 5 = \ f (x) dx. (I) Eksempel 1. La oss beregne arealet avgrenset av parablen y - 1 -x *, de rette linjene X = - Fj-, x = 1 og aksen O * (Fig. 86). i fig. 87. Fig. 86. 1 Her f (x) = 1 - n?, Grensene for integrasjon er a = - og t = 1, derfor 3) | _ 2 3V 2 / J 3 24 24 * Eksempel 2. Regn ut arealet avgrenset av sinusformet y = sinXy ved okseaksen og den rette linjen (fig. 87). Ved å bruke formel (I), får vi Л 2 S = J sinxdx = [-cos x] Q = 0 - (- 1) = lf Eksempel 3. Regn ut arealet avgrenset av buen til sinusoiden ^ y = sin jc, innesluttet mellom to tilstøtende skjæringspunkter med okseaksen (for eksempel mellom origo og punktet med abscissen i). Merk at det er klart fra geometriske betraktninger at dette området vil være dobbelt så stort som det forrige eksempelet. La oss imidlertid gjøre beregningene: i 5 = | s \ nxdx = [- cosx) * - - cos i - (- cos 0) = 1 + 1 = 2. o Faktisk, vår antagelse viste seg å være sann. Eksempel 4. Regn ut arealet avgrenset av en sinusformet og ^ av okseaksen i en periode (fig. 88). Foreløpige betraktninger gjør at vi kan anta at arealet vil være fire ganger større enn i pr. 2. Etter å ha gjort beregninger får vi imidlertid "i G, * i S - \ sin x dx = [- cos x] 0 = = - cos 2l - (- cos 0) = - 1 + 1 = 0. Dette resultatet krever avklaring. For å klargjøre essensen av saken, beregner vi også arealet avgrenset av den samme sinusformen y = sin l: og okseaksen i området fra l til 2i. Ved å bruke formel (I), får vi 2l $ 2l sin xdx = [- cosx] l = -cos 2ya ~) -c05ya = - 1-1 = -2. Dermed ser vi at dette området viste seg å være negativt. Sammenligner vi det med arealet beregnet i pr. 3, finner vi at deres absolutte verdier er de samme, men tegnene er forskjellige. Hvis vi bruker egenskap V (se kapittel XI, § 4), så får vi 2l I 2l J sin xdx = J sin * dx [sin x dx = 2 + (- 2) = 0 Det som skjedde i dette eksemplet er ikke tilfeldig . Alltid området under Ox-aksen, forutsatt at den uavhengige variabelen endres fra venstre til høyre, oppnås ved å beregne negative integraler. I dette kurset vil vi alltid vurdere umerkede ruter. Derfor vil svaret i det nettopp analyserte eksemplet være som følger: det nødvendige arealet er lik 2 + | -2 | = 4. Eksempel 5. La oss beregne arealet til OAB vist i fig. 89. Dette området er avgrenset av Ox-aksen, parabelen y = - xr og den rette linjen y - = -x + \. Kurvilineært trapesområde Søkeområdet OAV består av to deler: OAM og MAV. Siden punkt A er skjæringspunktet for parabelen og den rette linjen, vil vi finne dens koordinater ved å løse ligningssystemet 3 2 Y = mx. (vi trenger bare å finne abscissen til punkt A). Løser vi systemet, finner vi l; = ~. Derfor må arealet beregnes i deler, første kvadrat. OAM og deretter pl. MAV: .... G 3 2, 3 G xP 3 1/2 U 2. Qam- ^ x)