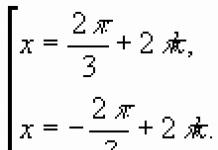Siden du kom hit har du sannsynligvis allerede sett denne formelen i læreboken

og lag et ansikt som dette:

Venn, ikke bekymre deg! Faktisk er alt enkelt å vanære. Du vil definitivt forstå alt. Bare en forespørsel - les artikkelen sakte, prøv å forstå hvert trinn. Jeg skrev så enkelt og tydelig som mulig, men du må fortsatt forstå ideen. Og sørg for å løse oppgavene fra artikkelen.

Hva er en kompleks funksjon?

Tenk deg at du flytter til en annen leilighet og derfor pakker tingene dine i store esker. Tenk deg at du trenger å samle noen små gjenstander, for eksempel skoleskrivemateriell. Hvis du bare kaster dem i en diger boks, så vil de blant annet gå seg vill. For å unngå dette legger du dem først for eksempel i en pose, som du så legger i en stor boks, hvorpå du forsegler den. Denne "komplekse" prosessen er vist i diagrammet nedenfor:

Det ser ut til, hva har matematikk med det å gjøre? Dessuten dannes en kompleks funksjon på AKKURAT samme måte! Bare vi "pakker" ikke notatbøker og penner, men \ (x \), mens "pakker" og "bokser" er forskjellige.

La oss for eksempel ta x og "pakke" den inn i en funksjon:

Som et resultat får vi selvfølgelig \ (\ cos⁡x \). Dette er vår "bag of things". Og nå legger vi det i en "boks" - vi pakker det for eksempel i en kubisk funksjon.

Hva vil skje til slutt? Ja, det stemmer, det blir en «pose med ting i boks», altså «kosinus til x i en kube».

Den resulterende konstruksjonen er en kompleks funksjon. Den skiller seg fra den enkle i det til én X brukes FLERE "påvirkninger" (pakker) på rad og det viser seg liksom "funksjon fra funksjon" - "emballasje i innpakning".

I skolekurset er det svært få typer av de samme "pakkene", bare fire:

La oss nå "pakke" x først inn i en eksponentiell funksjon med base 7, og deretter inn i en trigonometrisk funksjon. Vi får:

\ (x → 7 ^ x → tg⁡ (7 ^ x) \)

Og nå skal vi "pakke" x to ganger i trigonometriske funksjoner, først i, og deretter i:

\ (x → sin⁡x → ctg⁡ (sin⁡x) \)

Enkelt, ikke sant?

Skriv nå selve funksjonen, hvor x:
- først "pakket" inn i en cosinus, og deretter i en eksponentiell funksjon med en base \ (3 \);
- først til femte grad, og deretter til tangenten;
- først i logaritmen til grunntallet \ (4 \) , deretter til makten \ (- 2 \).

Se svarene på denne oppgaven på slutten av artikkelen.

Og kan vi "pakke" X ikke to, men tre ganger? Ikke noe problem! Og fire, og fem, og tjuefem ganger. For eksempel, her er en funksjon der x er "pakket" \ (4 \) ganger:

\ (y = 5 ^ (\ log_2⁡ (\ sin⁡ (x ^ 4)))) \)

Men slike formler vil ikke bli møtt i skolepraksis (studenter er mer heldige - de kan være mer kompliserte).

Pakke ut en kompleks funksjon

Se på forrige funksjon igjen. Kan du finne ut pakkesekvensen? Hva X ble dyttet inn i først, inn i hva så, og så videre helt til siste slutt. Det vil si hvilken funksjon er nestet i hvilken? Ta et stykke papir og skriv ned hva du synes. Du kan gjøre dette med en kjede med piler, som vi skrev ovenfor, eller på annen måte.

Nå er det riktige svaret: først ble x-en "pakket" inn i \ (4 \) - th potens, deretter ble resultatet pakket inn i en sinus, den ble på sin side plassert i logaritmen til grunnen \ (2 \ ), og til slutt ble hele denne konstruksjonen skjøvet inn i power fives.

Det vil si at det er nødvendig å avvikle sekvensen I OVERSIKTET REKKEFØLGE. Og her er et hint om hvordan du gjør det enklere: bare se på X-en - fra ham, så må du danse. La oss ta en titt på noen få eksempler.

For eksempel, her er en funksjon: \ (y = tg⁡ (\ log_2⁡x) \). Vi ser på X-en - hva skjer med ham først? Det er tatt fra ham. Og så? Tangensen til resultatet tas. Rekkefølgen vil være den samme:

\ (x → \ log_2⁡x → tg⁡ (\ log_2⁡x) \)

Et annet eksempel: \ (y = \ cos⁡ ((x ^ 3)) \). Vi analyserer - først ble x-en hevet til en kube, og deretter ble cosinus tatt fra resultatet. Følgelig vil sekvensen være: \ (x → x ^ 3 → \ cos⁡ ((x ^ 3)) \). Vær oppmerksom, funksjonen ser ut til å være lik den aller første (hvor med bilder). Men dette er en helt annen funksjon: her i x-kuben (det vil si \ (\ cos⁡ ((xxx))) \), og der, i kuben, cosinus \ (x \) (det vil si \) (\ cos⁡ x \ cos⁡x \ cos⁡x \)). Denne forskjellen oppstår fra forskjellige pakkesekvenser.

Det siste eksemplet (med viktig informasjon): \ (y = \ sin⁡ ((2x + 5)) \). Det er tydelig at her gjorde de først aritmetiske operasjoner med x, deretter tok de sinus fra resultatet: \ (x → 2x + 5 → \ sin⁡ ((2x + 5)) \). Og dette er et viktig poeng: til tross for at aritmetiske operasjoner ikke er funksjoner i seg selv, fungerer de også her som en måte å «pakke». La oss gå litt dypere inn i denne subtiliteten.

Som jeg sa ovenfor, i enkle funksjoner "pakkes" X en gang, og i komplekse funksjoner - to eller flere. Dessuten er enhver kombinasjon av enkle funksjoner (det vil si summen, forskjellen, multiplikasjonen eller divisjonen deres) også en enkel funksjon. For eksempel er \ (x ^ 7 \) en enkel funksjon og \ (ctg x \) er det også. Dette betyr at alle kombinasjonene deres er enkle funksjoner:

\ (x ^ 7 + ctg x \) - enkel,
\ (x ^ 7 ctg x \) - enkel,
\ (\ frac (x ^ 7) (ctg x) \) - enkel, etc.

Men hvis en funksjon til brukes på en slik kombinasjon, vil det allerede være en kompleks funksjon, siden det vil være to "pakninger". Se diagram:

Ok, kom på deg selv nå. Skriv sekvensen av "innpaknings"-funksjoner:
\ (y = cos (⁡ (sin⁡x)) \)
\ (y = 5 ^ (x ^ 7) \)
\ (y = arctg⁡ (11 ^ x) \)
\ (y = log_2⁡ (1 + x) \)
Svarene er igjen på slutten av artikkelen.

Interne og eksterne funksjoner

Hvorfor trenger vi å forstå funksjonshekking? Hva gir det oss? Faktum er at uten en slik analyse vil vi ikke være i stand til pålitelig å finne derivatene til funksjonene analysert ovenfor.

Og for å komme videre, trenger vi ytterligere to konsepter: interne og eksterne funksjoner. Dette er en veldig enkel ting, dessuten har vi faktisk allerede sortert dem ovenfor: hvis du husker analogien vår helt i begynnelsen, er den interne funksjonen en "pakke", og den eksterne er en "boks". De. det X-en er "viklet inn i" først er en intern funksjon, og det som den indre funksjonen er "pakket inn i" er allerede en ekstern. Vel, det er klart hvorfor - hun er utenfor, deretter ekstern.

I dette eksemplet: \ (y = tg⁡ (log_2⁡x) \), funksjonen \ (\ log_2⁡x \) er intern, og
- ekstern.

Og i denne: \ (y = \ cos⁡ ((x ^ 3 + 2x + 1)) \), \ (x ^ 3 + 2x + 1 \) er indre, og
- ekstern.

Følg den siste praksisen med å analysere komplekse funksjoner, og gå til slutt videre til hva det dreide seg om - vi vil finne derivatene av komplekse funksjoner:

Fyll ut de tomme feltene i tabellen:

Derivat av en kompleks funksjon

Bravo for oss, vi kom fortsatt til "sjefen" for dette emnet - faktisk avledet av en kompleks funksjon, og spesifikt til den veldig forferdelige formelen fra begynnelsen av artikkelen.

\ ((f (g (x))) "= f" (g (x)) \ cdot g "(x) \)

Denne formelen lyder slik:

Den deriverte av en kompleks funksjon er lik produktet av den deriverte av den ytre funksjonen med hensyn til den konstante indre funksjonen av den deriverte av den indre funksjonen.

Og se umiddelbart på analyseskjemaet "med ord" for å forstå hva du skal referere til:

Forhåpentligvis er begrepene "derivat" og "produkt" enkle. "Kompleks funksjon" - vi har allerede analysert den. En hake i "deriverten av en ekstern funksjon med hensyn til en ufravikelig indre". Hva det er?

Svar: dette er den vanlige deriverten av den eksterne funksjonen, der bare den eksterne funksjonen endres, og den interne forblir den samme. Fortsatt ikke klart? Ok, la oss bruke et eksempel.

Anta at vi har en funksjon \ (y = \ sin⁡ (x ^ 3) \). Det er tydelig at den indre funksjonen her \ (x ^ 3 \), og den ytre
... La oss nå finne den deriverte av det ytre med hensyn til det uforanderlige indre.

Det er absolutt umulig å løse fysiske problemer eller eksempler i matematikk uten kunnskap om den deriverte og metodene for å beregne den. Derivativ er et av de viktigste begrepene innen matematisk analyse. Vi bestemte oss for å vie dagens artikkel til dette grunnleggende emnet. Hva er en derivert, hva er dens fysiske og geometriske betydning, hvordan beregner man den deriverte av en funksjon? Alle disse spørsmålene kan kombineres til ett: hvordan forstå den deriverte?

Geometrisk og fysisk betydning av derivatet

La det være en funksjon f (x) gitt i et eller annet intervall (a, b) ... Punktene х og х0 tilhører dette intervallet. Når x endres, endres selve funksjonen. Endre et argument - forskjellen mellom verdiene x-x0 ... Denne forskjellen er skrevet som delta x og kalles argumentøkning. En endring eller økning av en funksjon er forskjellen i verdiene til en funksjon ved to punkter. Derivatdefinisjon:

Den deriverte av en funksjon i et punkt er grensen for forholdet mellom økningen av funksjonen ved et gitt punkt og økningen av argumentet når sistnevnte har en tendens til null.

Ellers kan det skrives slik:

Hva er vitsen med å finne en slik grense? Og her er hva:

den deriverte av funksjonen i et punkt er lik tangenten til vinkelen mellom OX-aksen og tangenten til grafen til funksjonen i dette punktet.

Den fysiske betydningen av derivatet: den deriverte av banen med hensyn til tid er lik hastigheten til den rettlinjede bevegelsen.

Faktisk, siden skoletiden, vet alle at hastighet er en privat vei. x = f (t) og tid t ... Gjennomsnittlig hastighet over en periode:

For å finne ut bevegelseshastigheten om gangen t0 du må beregne grensen:

Regel én: ta ut en konstant

Konstanten kan flyttes utenfor tegnet til den deriverte. Dessuten må det gjøres. Når du løser eksempler i matematikk, ta som regel - hvis du kan forenkle uttrykket, sørg for å forenkle .

Eksempel. La oss beregne den deriverte:

Regel to: derivert av summen av funksjoner

Den deriverte av summen av to funksjoner er lik summen av de deriverte av disse funksjonene. Det samme gjelder for den deriverte av funksjonsforskjellen.

Vi vil ikke gi et bevis på denne teoremet, men heller vurdere et praktisk eksempel.

Finn den deriverte av en funksjon:

Regel tre: derivert av produktet av funksjoner

Den deriverte av produktet av to differensierbare funksjoner beregnes med formelen:

Eksempel: finn den deriverte av en funksjon:

Løsning:

Det er viktig å si her om beregningen av deriverte av komplekse funksjoner. Den deriverte av en kompleks funksjon er lik produktet av den deriverte av denne funksjonen med hensyn til det mellomliggende argumentet med den deriverte av det mellomliggende argumentet med hensyn til den uavhengige variabelen.

I eksemplet ovenfor møter vi uttrykket:

I dette tilfellet er det mellomliggende argumentet 8x til femte potens. For å beregne den deriverte av et slikt uttrykk, beregner vi først den deriverte av den eksterne funksjonen med hensyn til det mellomliggende argumentet, og deretter multiplisere med den deriverte av det umiddelbare mellomargumentet med hensyn til den uavhengige variabelen.

Regel fire: kvotientderiverten av to funksjoner

Formel for å bestemme den deriverte av kvotienten til to funksjoner:

Vi prøvde å fortelle deg om derivater for dummies fra bunnen av. Dette emnet er ikke så enkelt som det høres ut, så vær advart: det er ofte fallgruver i eksemplene, så vær forsiktig når du beregner derivater.

For spørsmål om dette og andre temaer kan du kontakte studenttjenesten. I løpet av kort tid vil vi hjelpe deg med å løse den vanskeligste testen og håndtere oppgaver, selv om du aldri har drevet med å beregne derivater før.

I de «gamle» lærebøkene kalles det også «kjede»-regelen. Så hvis y = f (u), og u = φ (x), det er

y = f (φ (x))

kompleks - en sammensatt funksjon (sammensetning av funksjoner) da

hvor , etter beregning vurderes kl u = φ (x).

Legg merke til at vi her tok "forskjellige" komposisjoner fra de samme funksjonene, og resultatet av differensiering viste seg naturligvis å være avhengig av rekkefølgen på "blanding".

Kjederegelen strekker seg naturlig nok til en sammensetning av tre eller flere funksjoner. I dette tilfellet vil det være tre eller flere "lenker" i henholdsvis "kjeden" som utgjør derivatet. Det er også en analogi med multiplikasjon: "vi har" - en tabell med derivater; "Der" er multiplikasjonstabellen; "Vi" er en kjederegel og "det" er en multiplikasjonsregel med "kolonne". Når man beregner slike "komplekse" derivater, introduseres selvfølgelig ingen hjelpeargumenter (u¸v, etc.), men etter å ha notert seg selv antallet og rekkefølgen av funksjoner som er involvert i sammensetningen, "strenger" de de tilsvarende koblingene i den angitte rekkefølgen.

... Her utføres fem operasjoner med "x" for å få verdien av "igruka", det vil si at det er en sammensetning av fem funksjoner: "ekstern" (den siste av dem) - indikativ - e ; videre, i omvendt rekkefølge, den eksponentielle. (♦) 2; trigonometrisk synd (); beroligende. () 3 og til slutt logaritmisk ln. (). Så

De neste eksemplene vil være å "drepe fuglepar i en smekk": vi vil øve på å differensiere komplekse funksjoner og supplere tabellen med derivater av elementære funksjoner. Så:

4. For potensfunksjonen - y = x α - omskriver den ved å bruke den velkjente "grunnleggende logaritmiske identiteten" - b = e ln b - i formen x α = x α ln x vi oppnår

5. For en vilkårlig eksponentiell funksjon, ved å bruke samme teknikk, vil vi ha

6. For en vilkårlig logaritmisk funksjon, ved å bruke den velkjente formelen for overgangen til en ny base, får vi suksessivt

.

7. For å differensiere tangenten (cotangens), bruker vi regelen for å differensiere kvotienten:

For å få derivatene til de inverse trigonometriske funksjonene bruker vi relasjonen som derivatene til to gjensidige funksjoner tilfredsstiller, det vil si funksjonene φ (x) og f (x) forbundet med relasjonene:

Dette er forholdet

Det er fra denne formelen for gjensidig inverse funksjoner

og
,

Til slutt, la oss oppsummere disse og noen andre, like lett oppnåelige derivater, i følgende tabell.

På hvilken vi analyserte de enkleste derivatene, og ble også kjent med reglene for differensiering og noen teknikker for å finne derivater. Derfor, hvis du ikke er så veldig med avledet av funksjoner, eller noen punkter i denne artikkelen ikke er helt klare, så les først leksjonen ovenfor. Vær så snill, still inn på en seriøs stemning - materialet er ikke lett, men jeg vil likevel prøve å presentere det på en enkel og tilgjengelig måte.

I praksis må du forholde deg til den deriverte av en kompleks funksjon veldig ofte, jeg vil til og med si, nesten alltid, når du får oppgaver med å finne deriverte.

Vi ser i tabellen på regelen (nr. 5) for å differensiere en kompleks funksjon:

Forståelse. Først av alt, la oss ta hensyn til opptaket. Her har vi to funksjoner – og dessuten er funksjonen billedlig talt innebygd i funksjonen. En funksjon av denne typen (når en funksjon er nestet i en annen) kalles en kompleks funksjon.

Jeg vil kalle funksjonen ekstern funksjon og funksjonen - en indre (eller nestet) funksjon.

! Disse definisjonene er ikke teoretiske og skal ikke fremkomme i den endelige utformingen av oppgavene. Jeg bruker uformelle uttrykk "ekstern funksjon", "intern" funksjon kun for å gjøre det lettere for deg å forstå stoffet.

For å avklare situasjonen, vurder:

Eksempel 1

Finn den deriverte av en funksjon

Under sinusen har vi ikke bare bokstaven "X", men et heltallsuttrykk, så det vil ikke være mulig å finne den deriverte umiddelbart fra tabellen. Vi legger også merke til at det er umulig å bruke de fire første reglene her, det ser ut til å være en forskjell, men faktum er at du ikke kan "rive fra hverandre" en sinus:

I dette eksempelet, allerede fra mine forklaringer, er det intuitivt klart at en funksjon er en kompleks funksjon, og polynomet er en intern funksjon (nesting), og en ekstern funksjon.

Første skritt, som må utføres når man finner den deriverte av en kompleks funksjon, er det finne ut hvilken funksjon som er intern og hvilken som er ekstern.

Når det gjelder enkle eksempler, virker det klart at et polynom er nestet under sinusen. Men hva om alt ikke er åpenbart? Hvordan bestemme nøyaktig hvilken funksjon som er ekstern og hvilken som er intern? For å gjøre dette foreslår jeg å bruke følgende teknikk, som kan gjøres mentalt eller på et utkast.

Tenk deg at vi må beregne verdien av et uttrykk på en kalkulator (i stedet for ett, kan det være et hvilket som helst tall).

Hva skal vi beregne først? Først av alt du må utføre følgende handling:, så polynomet vil være en intern funksjon:

for det andre må finnes, så sinus vil være en ekstern funksjon:

Etter vi Fant ut med interne og eksterne funksjoner er det på tide å bruke regelen om differensiering av en kompleks funksjon .

Vi begynner å bestemme oss. Fra leksjonen Hvordan finner jeg den deriverte? vi husker at utformingen av løsningen av en hvilken som helst derivat alltid begynner slik - vi omslutter uttrykket i parentes og setter et slag øverst til høyre:

Først finn den deriverte av den eksterne funksjonen (sinus), se på tabellen over avledede funksjoner og legg merke til at. Alle tabellformler kan brukes selv om "x" er erstattet med et komplekst uttrykk, i dette tilfellet:

Merk at den indre funksjonen har ikke endret seg, vi rører den ikke.

Vel, det er ganske åpenbart det

Resultatet av å bruke formelen i det endelige designet ser det slik ut:

En konstant faktor plasseres vanligvis i begynnelsen av et uttrykk:

Hvis det er forvirring, skriv ned løsningen og les forklaringene på nytt.

Eksempel 2

Finn den deriverte av en funksjon

Eksempel 3

Finn den deriverte av en funksjon

Som alltid skriver vi ned:

La oss finne ut hvor vi har en ekstern funksjon, og hvor vi har en intern. For å gjøre dette, prøv (mentalt eller på et utkast) å beregne verdien av uttrykket på. Hva bør gjøres først? Først av alt må du beregne hva basen er lik: som betyr at polynomet er den interne funksjonen:

Og først da utføres eksponentieringen, derfor er potensfunksjonen en ekstern funksjon:

I henhold til formelen , først må du finne den deriverte av den eksterne funksjonen, i dette tilfellet graden. Vi ser etter den nødvendige formelen i tabellen:. Vi gjentar igjen: enhver tabellformel er gyldig ikke bare for "x", men også for et komplekst uttrykk... Dermed resultatet av å bruke regelen om differensiering av en kompleks funksjon neste:

Jeg understreker igjen at når vi tar den deriverte av den ytre funksjonen, endres ikke den indre funksjonen for oss:

Nå gjenstår det å finne et veldig enkelt derivat av den indre funksjonen og "gre" resultatet litt:

Eksempel 4

Finn den deriverte av en funksjon

Dette er et eksempel på en uavhengig løsning (svar på slutten av veiledningen).

For å konsolidere forståelsen av den deriverte av en kompleks funksjon, vil jeg gi et eksempel uten kommentarer, prøve å finne det ut på egen hånd, spekulere hvor er den eksterne og hvor er den interne funksjonen, hvorfor ble oppgavene løst på denne måten?

Eksempel 5

a) Finn den deriverte av funksjonen

b) Finn den deriverte av funksjonen

Eksempel 6

Finn den deriverte av en funksjon

Her har vi en rot, og for å differensiere roten må den representeres som en grad. Derfor bringer vi først funksjonen inn i en form som passer for differensiering:

Ved å analysere funksjonen kommer vi til den konklusjon at summen av tre ledd er en intern funksjon, og eksponentiering er en ekstern funksjon. Vi bruker regelen for differensiering av en kompleks funksjon :

Graden er igjen representert som en radikal (rot), og for den deriverte av den interne funksjonen bruker vi en enkel regel for å differensiere summen:

Klar. Du kan også bringe uttrykket til en fellesnevner i parentes og skrive alt ned i en brøk. Fint, selvfølgelig, men når det oppnås tungvinte lange derivater, er det bedre å ikke gjøre dette (det er lett å bli forvirret, gjøre en unødvendig feil, og det vil være upraktisk for læreren å sjekke).

Eksempel 7

Finn den deriverte av en funksjon

Dette er et eksempel på en uavhengig løsning (svar på slutten av veiledningen).

Det er interessant å merke seg at noen ganger, i stedet for regelen for å differensiere en kompleks funksjon, kan man bruke regelen for å differensiere kvotienten , men en slik løsning vil se uvanlig ut som en perversjon. Her er et typisk eksempel:

Eksempel 8

Finn den deriverte av en funksjon

Her kan du bruke regelen for å differensiere kvotienten , men det er mye mer lønnsomt å finne den deriverte gjennom regelen for differensiering av en kompleks funksjon:

Vi forbereder funksjonen for differensiering - vi flytter minus utenfor tegnet til den deriverte, og hever cosinus til telleren:

Cosinus er en intern funksjon, eksponentiering er en ekstern funksjon.
Vi bruker vår regel :

Finn den deriverte av den interne funksjonen, tilbakestill cosinus ned igjen:

Klar. I det betraktede eksemplet er det viktig å ikke bli forvirret i skiltene. Prøv forresten å løse det med regelen , må svarene samsvare.

Eksempel 9

Finn den deriverte av en funksjon

Dette er et eksempel på en uavhengig løsning (svar på slutten av veiledningen).

Så langt har vi sett på tilfeller der vi kun hadde ett vedlegg i en kompleks funksjon. I praktiske oppgaver kan du ofte finne derivater, der, som hekkende dukker, den ene inne i den andre, 3 eller til og med 4-5 funksjoner er nestet samtidig.

Eksempel 10

Finn den deriverte av en funksjon

La oss forstå vedleggene til denne funksjonen. Prøver å evaluere uttrykket ved å bruke testverdien. Hvordan vil vi regne med en kalkulator?

Først må du finne, noe som betyr at arcsine er den dypeste hekkingen:

Deretter bør denne arcsinen til en kvadrateres:

Og til slutt, heve 7 til makten:

Det vil si at vi i dette eksemplet har tre ulike funksjoner og to vedlegg, mens den innerste funksjonen er arcsinus, og den ytterste funksjonen er eksponentialfunksjonen.

Vi begynner å løse

I følge regelen først må du ta den deriverte av den eksterne funksjonen. Vi ser på tabellen med deriverte og finner den deriverte av eksponentialfunksjonen: Den eneste forskjellen er at i stedet for "x" har vi et komplekst uttrykk, som ikke negerer gyldigheten til denne formelen. Så resultatet av å bruke regelen om differensiering av en kompleks funksjon neste.

Komplekse funksjoner passer ikke alltid til definisjonen av en kompleks funksjon. Hvis det er en funksjon av formen y = sin x - (2 - 3) a r c t g x x 5 7 x 10 - 17 x 3 + x - 11, så kan den ikke betraktes som kompleks, i motsetning til y = sin 2 x.

Denne artikkelen vil vise konseptet med en kompleks funksjon og dens identifikasjon. La oss jobbe med formler for å finne den deriverte med eksempler på løsninger i konklusjonen. Bruken av tabellen over derivater og differensieringsregelen reduserer tiden det tar å finne derivatet betydelig.

Grunnleggende definisjoner

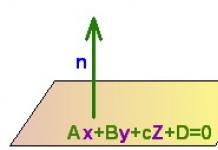
Definisjon 1

En kompleks funksjon er en funksjon hvis argument også er en funksjon.

Det er betegnet på denne måten: f (g (x)). Vi har at funksjonen g (x) regnes som et argument til f (g (x)).

Definisjon 2

Hvis det er en funksjon f og er en cotangensfunksjon, så er g (x) = ln x en naturlig logaritmefunksjon. Vi får at den komplekse funksjonen f (g (x)) vil bli skrevet som arctan (lnx). Eller en funksjon f, som er en funksjon hevet til 4. potens, hvor g (x) = x 2 + 2 x - 3 regnes som en hel rasjonell funksjon, vi får at f (g (x)) = (x 2 + 2 x - 3) 4 ...

Det er klart at g (x) kan være vanskelig. Fra eksempelet y = sin 2 x + 1 x 3 - 5, kan du se at verdien av g har en terningrot med en brøk. Dette uttrykket er tillatt betegnet som y = f (f 1 (f 2 (x))). Derfra har vi at f er sinusfunksjonen, og f 1 er funksjonen plassert under kvadratroten, f 2 (x) = 2 x + 1 x 3 - 5 er en rasjonell brøkfunksjon.

Definisjon 3

Hekkegraden bestemmes av et hvilket som helst naturlig tall og skrives som y = f (f 1 (f 2 (f 3 (... (F n (x)))))).

Definisjon 4

Konseptet funksjonssammensetning refererer til antall nestede funksjoner etter tilstanden til problemet. For løsningen, formelen for å finne den deriverte av en kompleks funksjon av formen

(f (g (x))) "= f" (g (x)) g "(x)

Eksempler av

Eksempel 1

Finn den deriverte av en kompleks funksjon av formen y = (2 x + 1) 2.

Løsning

Ved betingelsen kan du se at f er en kvadreringsfunksjon, og g (x) = 2 x + 1 regnes som en lineær funksjon.

La oss bruke den deriverte formelen for en kompleks funksjon og skrive:

f "(g (x)) = ((g (x)) 2)" = 2 · (g (x)) 2 - 1 = 2 · g (x) = 2 · (2 ​​​​x + 1); g "(x) = (2 x + 1)" = (2 x) "+ 1" = 2 x "+ 0 = 2 1 x 1 - 1 = 2 ⇒ (f (g (x))) "= f " (g (x)) g "(x) = 2 (2 x + 1) 2 = 8 x + 4

Det er nødvendig å finne en derivert med en forenklet opprinnelig form av funksjonen. Vi får:

y = (2 x + 1) 2 = 4 x 2 + 4 x + 1

Derfor har vi det

y "= (4 x 2 + 4 x + 1)" = (4 x 2) "+ (4 x)" + 1 "= 4 · (x 2)" + 4 · (x) "+ 0 = = 4 2 x 2 - 1 + 4 1 x 1 - 1 = 8 x + 4

Resultatene stemte.

Når man skal løse problemer av denne typen, er det viktig å forstå hvor funksjonen til formen f og g (x) vil ligge.

Eksempel 2

Du bør finne de deriverte av komplekse funksjoner av formen y = sin 2 x og y = sin x 2.

Løsning

Den første notasjonen til funksjonen sier at f er en kvadreringsfunksjon og g (x) er en sinusfunksjon. Da får vi det

y "= (sin 2 x)" = 2 sin 2 - 1 x (sin x) "= 2 sin x cos x

Den andre oppføringen viser at f er en sinusfunksjon, og g (x) = x 2 betegner vi en potensfunksjon. Det følger at produktet av en kompleks funksjon kan skrives som

y "= (sin x 2)" = cos (x 2) (x 2) "= cos (x 2) 2 x 2 - 1 = 2 x cos (x 2)

Formelen for den deriverte y = f (f 1 (f 2 (f 3 (... (Fn (x)))))) vil bli skrevet som y "= f" (f 1 (f 2 (f 3 ( ... ( fn (x))))) f 1 "(f 2 (f 3 (... (fn (x))))) f 2" (f 3 (.. (fn (x))) )) ·. ... ... · F n "(x)

Eksempel 3

Finn den deriverte av funksjonen y = sin (ln 3 a r c t g (2 x)).

Løsning

Dette eksemplet viser kompleksiteten av skrive- og lokaliseringsfunksjoner. Da angir y = f (f 1 (f 2 (f 3 (f 4 (x))))), hvor f, f 1, f 2, f 3, f 4 (x) er en sinusfunksjon, en funksjon av heving i 3 grader, funksjon med logaritme og base e, arctangent funksjon og lineær.

Fra formelen for definisjonen av en kompleks funksjon har vi det

y "= f" (f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x)))) f 2" (f 3 (f 4 (x))) f 3 "(f 4 (x)) f 4" (x)

Vi får hva vi skal finne

1. f "(f 1 (f 2 (f 3 (f 4 (x))))) som sinusderiverte i henhold til tabellen over deriverte, deretter f" (f 1 (f 2 (f 3 (f 4 (x)) ))) ) = cos (ln 3 arctan (2 x)).
2. f 1 "(f 2 (f 3 (f 4 (x)))) som den deriverte av potensfunksjonen, deretter f 1" (f 2 (f 3 (f 4 (x)))) = 3 ln 3 - 1 arktan (2 x) = 3 ln 2 arktan (2 x).
3. f 2 "(f 3 (f 4 (x))) som den deriverte av logaritmikken, deretter f 2" (f 3 (f 4 (x))) = 1 a r c t g (2 x).
4. f 3 "(f 4 (x)) som derivatet av arctangensen, deretter f 3" (f 4 (x)) = 1 1 + (2 x) 2 = 1 1 + 4 x 2.
5. Når du finner den deriverte f 4 (x) = 2 x, trekk 2 utenfor tegnet til den deriverte ved å bruke formelen for den deriverte av en potensfunksjon med en eksponent lik 1, deretter f 4 "(x) = (2 x) " = 2 x "= 2 1 x 1 - 1 = 2.

Vi kombinerer mellomresultatene og får det

y "= f" (f 1 (f 2 (f 3 (f 4 (x))))) f 1 "(f 2 (f 3 (f 4 (x)))) f 2" (f 3 (f 4 (x))) f 3 "(f 4 (x)) f 4" (x) = = cos (ln 3 arctan (2 x)) 3 ln 2 arctan (2 x) 1 arctan (2 x) 1 1 + 4 x 2 2 = = 6 cos (ln 3 arctan (2 x)) ln 2 arctan (2 x) arctan (2 x) (1 + 4 x 2)

Analysen av slike funksjoner minner om hekkende dukker. Differensieringsregler kan ikke alltid brukes eksplisitt ved å bruke en tabell med derivater. Det er ofte nødvendig å bruke en formel for å finne deriverte av komplekse funksjoner.

Det er noen forskjeller mellom et komplekst syn og en kompleks funksjon. Med en åpenbar evne til å skille dette, vil det være spesielt enkelt å finne derivater.

Eksempel 4

Det er nødvendig å vurdere å gi et lignende eksempel. Hvis det er en funksjon av formen y = t g 2 x + 3 t g x + 1, kan den betraktes som en kompleks form g (x) = t g x, f (g) = g 2 + 3 g + 1. Åpenbart er det nødvendig å bruke en formel for et komplekst derivat:

f "(g (x)) = (g 2 (x) + 3 g (x) + 1)" = (g 2 (x)) "+ (3 g (x))" + 1 "= = 2 · g 2 - 1 (x) + 3 · g "(x) + 0 = 2 g (x) + 3 · 1 · g 1 - 1 (x) = = 2 g (x) + 3 = 2 tgx + 3; g "(x) = (tgx)" = 1 cos 2 x ⇒ y "= (f (g (x)))" = f "(g (x)) g" (x) = (2 tgx + 3 ) 1 cos 2 x = 2 tgx + 3 cos 2 x

En funksjon av formen y = t g x 2 + 3 t g x + 1 anses ikke som vanskelig, siden den har summen av t g x 2, 3 t g x og 1. Imidlertid regnes t g x 2 som en kompleks funksjon, da får vi en potensfunksjon av formen g (x) = x 2 og f, som er en funksjon av tangenten. For å gjøre dette er det nødvendig å skille etter mengden. Det skjønner vi

y "= (tgx 2 + 3 tgx + 1)" = (tgx 2) "+ (3 tgx)" + 1 "= = (tgx 2)" + 3 · (tgx) "+ 0 = (tgx 2)" + 3 cos 2 x

Vi fortsetter med å finne den deriverte av en kompleks funksjon (t g x 2) ":

f "(g (x)) = (brun (g (x)))" = 1 cos 2 g (x) = 1 cos 2 (x 2) g "(x) = (x 2)" = 2 x 2 - 1 = 2 x ⇒ (tgx 2) "= f" (g (x)) g "(x) = 2 x cos 2 (x 2)

Vi får at y "= (t g x 2 + 3 t g x + 1)" = (t g x 2) "+ 3 cos 2 x = 2 x cos 2 (x 2) + 3 cos 2 x

Komplekse funksjoner kan inkluderes i komplekse funksjoner, og komplekse funksjoner i seg selv kan være komplekse funksjoner.

Eksempel 5

Tenk for eksempel på en kompleks funksjon av formen y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1)

Denne funksjonen kan representeres på formen y = f (g (x)), hvor verdien av f er en funksjon av logaritmen til grunntallet 3, og g (x) regnes som summen av to funksjoner av formen h ( x) = x 2 + 3 cos 3 (2 x + 1) + 7 ex 2 + 3 3 og k (x) = ln 2 x (x 2 + 1). Åpenbart er y = f (h (x) + k (x)).

Tenk på funksjonen h (x). Dette er forholdet l (x) = x 2 + 3 cos 3 (2 x + 1) + 7 til m (x) = e x 2 + 3 3

Vi har at l (x) = x 2 + 3 cos 2 (2 x + 1) + 7 = n (x) + p (x) er summen av to funksjoner n (x) = x 2 + 7 og p ( x) = 3 cos 3 (2 x + 1), hvor p (x) = 3 p 1 (p 2 (p 3 (x))) er en kompleks funksjon med en numerisk koeffisient 3, og p 1 er en kubende funksjon , p 2 som en cosinus funksjon, p 3 (x) = 2 x + 1 - en lineær funksjon.

Vi fikk at m (x) = ex 2 + 3 3 = q (x) + r (x) er summen av to funksjoner q (x) = ex 2 og r (x) = 3 3, hvor q (x) = q 1 (q 2 (x)) er en kompleks funksjon, q 1 er en funksjon med eksponentiell funksjon, q 2 (x) = x 2 er en potensfunksjon.

Dette viser at h (x) = l (x) m (x) = n (x) + p (x) q (x) + r (x) = n (x) + 3 p 1 (p 2 ( p 3) (x))) q 1 (q 2 (x)) + r (x)

Overgang til et uttrykk på formen k (x) = ln 2 x s 2 (x)) med rasjonelt heltall t (x) = x 2 + 1, hvor s 1 er kvadratingsfunksjonen, og s 2 (x) = ln x er logaritmisk med grunntallet e.

Det følger at uttrykket har formen k (x) = s (x) t (x) = s 1 (s 2 (x)) t (x).

Da får vi det

y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 ex 2 + 3 3 + ln 2 x (x 2 + 1) = = fn (x) + 3 p 1 (p 2 (p 3 ( x))) q 1 (q 2 (x)) = r (x) + s 1 (s 2 (x)) t (x)

Ved funksjonsstrukturer ble det klart hvordan og hvilke formler som skulle brukes for å forenkle et uttrykk når man differensierer det. For å gjøre deg kjent med slike problemer og for konseptet med deres løsning, er det nødvendig å vende seg til punktet for differensiering av funksjonen, det vil si å finne dens derivat.

Hvis du oppdager en feil i teksten, velg den og trykk Ctrl + Enter