How to find roots in a gap in trigonometry. Finding the roots of the equation that belong to the segment. Different ways to select roots

Problem number 1

The logic is simple: we will act as we did before, despite the fact that now the trigonometric functions have a more complex argument!

If we were to solve an equation of the form:

Then we would write down the following answer:

Or (since)

But now we have the following expression in our role:

Then you can write:

Our goal with you is to make the left stand simply, without any "impurities"!

Let's get rid of them gradually!

First, we remove the denominator at: for this we multiply our equality by:

Now let's get rid of it by dividing both parts into it:

Now let's get rid of the eight:

The resulting expression can be written as 2 series of solutions (by analogy with a quadratic equation, where we either add or subtract the discriminant)

We need to find the largest negative root! It is clear that it is necessary to sort out.

Consider the first series first:

It is clear that if we take, then as a result we will get positive numbers, and they are not of interest to us.

So you need to take it negative. Let.

When the root is already:

And we need to find the largest negative one !! It means that it no longer makes sense to go in the negative direction. And the largest negative root for this series will be.

Now let's look at the second series:

And again we substitute:, then:

Not interested!

Then it doesn't make sense to increase anymore! We will reduce! Let, then:

Fits!

Let. Then

Then - the largest negative root!

Answer:

Problem number 2

Again we solve, regardless of the complex cosine argument:

Now we express to the left again:

We multiply both sides by

We divide both sides into

All that is left is to move it to the right, changing its sign from minus to plus.

We again have 2 series of roots, one with and the other with.

We need to find the largest negative root. Consider the first series:

It is clear that we will receive the first negative root at, it will be equal to and will be the largest negative root in 1 series.

For the second series

The first negative root will also be obtained at and will be equal to. Since, then is the largest negative root of the equation.

Answer: .

Problem number 3

Solve regardless of the complex tangent argument.

That seems to be nothing complicated, right?

As before, we express on the left side:

Well, that's great, there is only one series of roots here! Find the largest negative one again.

It is clear that it turns out if we put. And this root is equal.

Answer:

Now try to solve the following problems yourself.

Homework or 3 tasks for an independent solution.

Decisions-shi-te equation.
Decisions-shi-te equation.
In the ot-ve-those na-pi-shi-te, the smallest po-li-tel-root.
Decisions-shi-te equation.
In the ot-ve-those na-pi-shi-te, the smallest po-li-tel-root.

Ready? Checking. I will not describe in detail the entire solution algorithm, it seems to me that enough attention has already been paid to it above.

Well, is everything correct? Oh, those nasty sinuses, there are always some troubles with them!

Well, now you can solve the simplest trigonometric equations!

Check solutions and answers:

Problem number 1

Let us express

The smallest positive root is obtained if we put, since, then

Answer:

Problem number 2

The smallest positive root is obtained when.

It will be equal.

Answer: .

Problem number 3

When we get, when we get.

Answer: .

This knowledge will help you solve many of the problems that you will face in the exam.

If you are applying for a grade of "5", then you just need to go to reading the article for middle level, which will be devoted to solving more complex trigonometric equations (task C1).

AVERAGE LEVEL

In this article I will describe solving trigonometric equations of a more complex type and how to select their roots. Here I will build on the following topics:

Trigonometric equations for the entry level (see above).

More complex trigonometric equations are the basis of more complex problems. In them, it is required both to solve the equation itself in general form, and to find the roots of this equation belonging to a certain specified interval.

Solving trigonometric equations comes down to two subtasks:

Equation solution
Selection of roots

It should be noted that the latter is not always required, but still selection is required in most examples. And if it is not required, then you can rather sympathize - this means that the equation is quite complicated in itself.

My experience in parsing C1 tasks shows that they are usually divided into these categories.

Four categories of tasks of increased complexity (formerly C1)

Equations that reduce to factorization.
Equations reducing to the form.
Equations Solved by Variable Change.
Equations requiring additional selection of roots due to irrationality or denominator.

To put it simply: if you come across one of the first three types of equations then consider yourself lucky. For them, as a rule, you additionally need to pick up roots belonging to a certain interval.

If you come across an equation of type 4, then you are less fortunate: you need to tinker with it a little longer and more closely, but quite often it does not require additional selection of roots in it. Nevertheless, I will analyze this type of equations in the next article, and this one will be devoted to solving equations of the first three types.

Factoring Equations

The most important thing to remember in order to solve equations of this type is

As practice shows, as a rule, this knowledge is sufficient. Let's look at some examples:

Example 1. Equation Reducing to Factorization Using Reduction Formulas and Double Angle Sine

Res-shi-te equation
Nay-di-te all the roots of this equation

Here, as I promised, the casting formulas work:

Then my equation will look like this:

Then my equation will take the following form:

A shortsighted student might say: and now I will shorten both parts by, get the simplest equation and enjoy life! And it will be bitterly mistaken!

REMEMBER: NEVER REDUCE BOTH PARTS OF THE TRIGONOMETRIC EQUATION BY A FUNCTION CONTAINING AN UNKNOWN! SO YOU LOSE ROOTS!

So what do you do? Yes, everything is simple, move everything in one direction and take out the common factor:

Well, we factor it into factors, hurray! Now we decide:

The first equation has roots:

And the second:

This completes the first part of the problem. Now we need to select the roots:

The gap is like this:

Or it can also be written like this:

Well, let's take the roots:

First, let's work with the first series (and it's easier, what can we say!)

Since our interval is entirely negative, there is no need to take non-negative ones, all the same they will give non-negative roots.

Let's take, then - a bit too much, does not fit.

Let, then - did not hit again.

One more attempt - then - there is, hit! First root found!

I shoot again: then - I hit it again!

Well, one more time:: - this is already a flight.

So from the first series 2 roots belong to the interval:.

We are working with the second series (we are building to a degree according to the rule):

Undershoot!

Undershoot again!

Again undershoot!

Got it!

Flight!

Thus, the following roots belong to my span:

It is by this algorithm that we will solve all other examples. Let's practice together with one more example.

Example 2. An equation that reduces to factorization using reduction formulas

Solve the equation

Solution:

Again the notorious casting formulas:

Again, do not try to reduce!

The first equation has roots:

And the second:

Now search for roots again.

I'll start with the second series, I already know everything about it from the previous example! Look and make sure the roots belonging to the gap are as follows:

Now the first episode and it is simpler:

If - fits

If - is also good

If - already a flight.

Then the roots will be as follows:

Independent work. 3 equations.

Well, is the technique clear to you? Solving trigonometric equations doesn't seem so difficult anymore? Then quickly solve the following problems yourself, and then you and I will solve other examples:

Solve the equation
Nay-di-those are all the roots of this equation, attached to the interval.
Res-shi-te equation
Indicate the roots of the equation
Res-shi-te equation
Nay-di-those are all the roots of this equation-non-niy, attached-over-le-zha-shi-pro-me-zhut-ku.

Equation 1.

And again the casting formula:

First series of roots:

Second series of roots:

Starting selection for the gap

Answer: , .

Equation 2. Checking independent work.

Quite a tricky grouping into factors (I'll use the double angle sine formula):

then or

This is a general solution. Now we need to select the roots. The trouble is that we cannot tell the exact value of the angle, the cosine of which is equal to one quarter. Therefore, I cannot just get rid of the arccosine - this is such a shame!

What I can do is figure out what so how, then.

Let's make a table: interval:

Well, through painful searches, we came to the disappointing conclusion that our equation has one root at the indicated interval: \ displaystyle arccos \ frac (1) (4) -5 \ pi

Equation 3. Checking independent work.

A frightening equation. However, it can be solved quite simply by applying the double angle sine formula:

Reduce by 2:

Let's group the first term with the second and the third with the fourth and take out the common factors:

It is clear that the first equation has no roots, and now consider the second:

In general, I was going to dwell on the solution of such equations a little later, but since it turned up, then there is nothing to do, it is necessary to solve ...

Equations of the form:

This equation is solved by dividing both parts by:

Thus, our equation has a single series of roots:

It is necessary to find those of them that belong to the interval:.

Let's build a table again, as I did earlier:

Answer: .

Equations that reduce to the form:

Well, now is the time to move on to the second batch of equations, especially since I have already blabbed what the solution of trigonometric equations of a new type consists of. But it will not be superfluous to repeat that an equation of the form

It is solved by dividing both parts by the cosine:

Res-shi-te equation
Indicate the roots of the equation-not-nia, when-over-lying-from-cutting.
Res-shi-te equation
Indicate the roots of the equation-not-nia, when-over-le-zha-shi-pro-me-zhut-ku.

Example 1.

The first is very simple. Move to the right and apply the double angle cosine formula:

Aha! Equation of the form:. I divide both parts into

We do the sifting of the roots:

Gap:

Answer:

Example 2.

Everything is also pretty trivial: let's expand the brackets on the right:

Basic trigonometric identity:

Double angle sine:

We finally get:

Root dropout: gap.

Answer: .

Well, how do you like the technique, is it not too complicated? I hope not. We can immediately make a reservation: in their pure form, equations, which immediately reduce to an equation for the tangent, are quite rare. Typically, this transition (division by cosine) is only part of a more complex problem. Here's an example for you to practice:

Res-shi-te equation
Nay-di-those are all the roots of this equation-not-nia, attached-over-le-zha-shi-ku.

Let's check:

The equation is solved immediately, it is enough to divide both parts into:

Root dropout:

Answer: .

One way or another, we have yet to meet with equations of the kind that we have just analyzed. However, it is too early for us to round off: there is one more "layer" of equations that we have not analyzed. So:

Solving trigonometric equations by changing a variable

Everything is transparent here: we look closely at the equation, simplify it as much as possible, make a substitution, solve, make a reverse substitution! In words, everything is very easy. Let's see in action:

Example.

Solve the equation:.
Nay-di-those are all the roots of this equation-not-nia, attached-over-le-zha-shi-ku.

Well, here the replacement itself begs to be in our hands!

Then our equation will turn into this:

The first equation has roots:

And the second is these:

Now we will find the roots belonging to the interval

Answer: .

Let's go over a slightly more complex example together:

Res-shi-te equation
Indicate the roots of the given equation-non-niy, when-over-le-za-shi-n-e-zhut-ku.

Here the replacement is not immediately visible, moreover, it is not very obvious. Let's think first: what can we do?

For example, we can imagine

And at the same time

Then my equation will take the form:

Now attention, focus:

Let's divide both sides of the equation by:

Suddenly you and I got a quadratic equation for! Let's make a replacement, then we get:

The equation has the following roots:

Nasty second series of roots, but it can't be helped! We select the roots in the interval.

We also need to consider that

Since and, then

Answer:

To consolidate, before you solve the problems yourself, here's another exercise for you:

Res-shi-te equation
Nay-di-those are all the roots of this equation-non-niy, attached-over-le-zha-shi-pro-me-zhut-ku.

Here you need to keep your eyes open: we now have denominators that can be zero! Therefore, you need to be especially attentive to the roots!

First of all, I need to transform the equation so that I can make a suitable substitution. I can't think of anything better right now than to rewrite the tangent in terms of sine and cosine:

Now I will go from cosine to sine by basic trigonometric identity:

And finally, I will bring everything to a common denominator:

Now I can go to the equation:

But at (that is, at).

Everything is now ready for replacement:

Then either

However, please note that if, then at the same time!

Who suffers from this? The trouble with the tangent, it is undefined when the cosine is zero (division by zero).

Thus, the roots of the equation are as follows:

Now we sift out the roots in the interval:


	- fits
	- brute force

Thus, our equation has a single root in the interval, and it is equal to.

You see: the appearance of the denominator (as well as the tangent, leads to certain difficulties with the roots! Here you need to be more careful!).

Well, you and I have almost finished the analysis of trigonometric equations, there is very little left - to independently solve two problems. Here they are.

Solve the equation
Nay-di-those are all the roots of this equation-not-nia, attached-over-le-zha-shi-ku.
Res-shi-te equation
Indicate the roots of this equation, attached to the cut.

Decided? Not very difficult? Let's check:

We work according to the reduction formulas:
Substitute into the equation:
Let's rewrite everything in terms of cosines, so that it is more convenient to do the replacement:
Now it's easy to make the replacement:
It is clear that this is an extraneous root, since the equation has no solutions. Then:
We are looking for the roots we need in the interval
Answer: .
Here the replacement is immediately visible:
Then either

- fits! - fits!
- fits! - fits!
- lot! - a lot too!
Answer:

Well, now that's it! But the solution of trigonometric equations does not end there, we are left with the most difficult cases: when there is irrationality in the equations or all sorts of "complex denominators". We will consider how to solve such tasks in the article for the advanced level.

ADVANCED LEVEL

In addition to the trigonometric equations discussed in the previous two articles, we will consider another class of equations that require even more careful analysis. These trigonometric examples contain either irrationality or a denominator, which makes them more difficult to analyze.... However, you may well come across these equations in Part C of the exam paper. However, there is a silver lining: for such equations, as a rule, the question of which of its roots belongs to a given interval is not raised. Let's not beat around the bush, but just trigonometric examples.

Example 1.

Solve the equation and find the roots that belong to the segment.

Solution:

We have a denominator that should not be zero! Then solving this equation is the same as solving the system

Let's solve each of the equations:

And now the second:

Now let's take a look at the series:

It is clear that the option does not suit us, since in this case the denominator is zeroed out (see the formula for the roots of the second equation)

If, however, then everything is in order, and the denominator is not zero! Then the roots of the equation are as follows:,.

Now we select the roots belonging to the interval.


	- does not fit	- fits
	- fits	- fits
	brute force	brute force

Then the roots are as follows:

You see, even the appearance of a small noise in the form of a denominator significantly affected the solution of the equation: we dropped a series of roots that zero the denominator. The situation can be even more difficult if you come across trigonometric examples that have irrationality.

Example 2.

Solve the equation:

Solution:

Well, at least there is no need to select the roots and that's good! Let's first solve the equation, regardless of irrationality:

Is that all? No, alas, it would be too easy! It must be remembered that only non-negative numbers can be under the root. Then:

The solution to this inequality:

Now it remains to find out if some of the roots of the first equation have accidentally got there where the inequality is not satisfied.

To do this, you can again use the table:


	: , but	Not!
		Yes!
		Yes!

Thus, one of the roots "fell out" from me! It turns out if you put it. Then the answer can be written as follows:

Answer:

You see, the root requires even closer attention! To complicate matters: now let me have a trigonometric function under the root.

Example 3.

As before: first we will solve each separately, and then we will think about what we have done.

Now the second equation:

Now the most difficult thing is to find out if negative values under the arithmetic root are obtained if we substitute the roots from the first equation there:

The number should be understood as radians. Since radians are about degrees, radians are about degrees. This is the corner of the second quarter. What is the sign of the cosine of the second quarter? Minus. And the sine? A plus. So what can be said about the expression:

It's less than zero!

This means that it is not the root of the equation.

Now it's the turn.

Let's compare this number with zero.

Cotangent is a function decreasing in 1 quarter (the smaller the argument, the larger the cotangent). radians are roughly degrees. In the same time

since, then, and hence
,

Answer: .

Could it be even more difficult? You are welcome! It will be more difficult if the trigonometric function is still under the root, and the second part of the equation is again the trigonometric function.

The more trigonometric examples the better, see further:

Example 4.

The root is not suitable due to the limited cosine

Now the second:

At the same time, by definition of the root:

We must remember the unit circle: namely, those quarters where the sine is less than zero. What quarters are they? Third and fourth. Then we will be interested in those solutions of the first equation that lie in the third or fourth quarter.

The first series produces roots at the intersection of the third and fourth quarters. The second series, which is diametrically opposite to it, gives rise to roots lying on the border of the first and second quarters. Therefore, this series does not suit us.

Answer: ,

And again trigonometric examples with "difficult irrationality"... Not only do we have the trigonometric function under the root again, but now it is also in the denominator!

Example 5.

Well, nothing can be done - we act as before.

Now we work with the denominator:

I don’t want to solve trigonometric inequality, and therefore I’ll act cunningly: I will take and substitute my series of roots into the inequality:

If - even, then we have:

since, then all the angles of the view lie in the fourth quarter. And again the sacred question: what is the sinus sign in the fourth quarter? Negative. Then the inequality

If it is odd, then:

Which quarter does the corner lie in? This is the corner of the second quarter. Then all the corners are again the corners of the second quarter. The sinus is positive there. Just what you need! Hence, the series:

Fits!

Deal with the second series of roots in the same way:

We substitute in our inequality:

If - even, then

First quarter corners. The sinus is positive there, so the series is suitable. Now if - odd, then:

also fits!

Well, now we write down the answer!

Answer:

Well, this was perhaps the most time consuming case. Now I offer you problems for your own solution.

Workout

Solve and find all the roots of the equation that belong to the segment.

Solutions:

First equation:
or
ODZ root:
Second equation:
Selecting roots that belong to the gap
Answer:

Or
or
But

Consider:. If - even, then
- does not fit!
If - odd,: - fits!
This means that our equation has the following series of roots:
or
Selection of roots in the interval:


	- does not fit	- fits
	- fits	- lot
	- fits	lot

Answer: , .

Or
Since, when the tangent is not defined. We immediately discard this series of roots!

Second part:

At the same time, according to ODZ, it is required that

We check the roots found in the first equation:

If the sign is:

First quarter corners where the tangent is positive. Doesn't fit!
If the sign is:

Fourth quarter angle. There the tangent is negative. Fits. We write down the answer:

Answer: , .

We have covered complex trigonometric examples together in this article, but you should solve the equations yourself.

SUMMARY AND BASIC FORMULAS

A trigonometric equation is an equation in which the unknown is strictly under the sign of the trigonometric function.

There are two ways to solve trigonometric equations:

The first way is using formulas.

The second way is through the trigonometric circle.

Allows you to measure angles, find their sines, cosines, and more.

Preparation for the profile level of the unified state exam in mathematics. Useful materials on trigonometry, large theoretical video lectures, video analyzes of problems and a selection of assignments from past years.

Useful materials

Video selections and online courses

Trigonometric formulas

Geometric illustration of trigonometric formulas

Arc functions. Simplest trigonometric equations

Trigonometric Equations

The necessary theory for solving problems.
a) Solve the equation $ 7 \ cos ^ 2 x - \ cos x - 8 = 0 $.
b) Find all roots of this equation that belong to the interval $ \ left [- \ dfrac (7 \ pi) (2); - \ dfrac (3 \ pi) (2) \ right] $.
a) Solve the equation $ \ dfrac (6) (\ cos ^ 2 x) - \ dfrac (7) (\ cos x) + 1 = 0 $.
b) Find all roots of this equation that belong to the interval $ \ left [-3 \ pi; - \ pi \ right] $.
Solve the equation $ \ sin \ sqrt (16 - x ^ 2) = \ dfrac12 $.
a) Solve the equation $ 2 \ cos 2x - 12 \ cos x + 7 = 0 $.
b) Find all the roots of this equation that belong to the interval $ \ left [- \ pi; \ dfrac (5 \ pi) (2) \ right] $.
a) Solve the equation $ \ dfrac (5) (\ mathrm (tg) ^ 2 x) - \ dfrac (19) (\ sin x) + 17 = 0 $.
Solve the equation $ \ dfrac (2 \ cos ^ 3 x + 3 \ cos ^ 2 x + \ cos x) (\ sqrt (\ mathrm (ctg) x)) = 0 $.
Solve the equation $ \ dfrac (\ mathrm (tg) ^ 3x - \ mathrm (tg) x) (\ sqrt (- \ sin x)) = 0 $.
b) Find all roots of this equation that belong to the interval $ \ left [- \ dfrac (5 \ pi) (2); - \ pi \ right) $.
a) Solve the equation $ \ cos 2x = \ sin \ left (\ dfrac (3 \ pi) (2) - x \ right) $.
b) Find all roots of this equation that belong to the interval $ \ left [\ dfrac (3 \ pi) (2); \ dfrac (5 \ pi) (2) \ right] $.
a) Solve the equation $ 2 \ sin ^ 2 \ left (\ dfrac (3 \ pi) (2) + x \ right) = \ sqrt3 \ cos x $.
b) Find all roots of this equation that belong to the interval $ \ left [- \ dfrac (7 \ pi) (2); -2 \ pi \ right] $.

Video analysis of tasks

b) Find all the roots of this equation that belong to the segment $ \ left [\ sqrt (3); \ sqrt (20) \ right] $.

b) Find all roots of this equation that belong to the segment $ \ left [- \ dfrac (9 \ pi) (2); -3 \ pi \ right] $.

b) Find all the roots of this equation that belong to the segment $ \ left [- \ sqrt (3); \ sqrt (30) \ right] $.

a) Solve the equation $ \ cos 2x = 1 - \ cos \ left (\ dfrac (\ pi) (2) - x \ right) $.
b) Find all roots of this equation that belong to the interval $ \ left [- \ dfrac (5 \ pi) (2); - \ pi \ right) $.

a) Solve the equation $ \ cos ^ 2 (\ pi - x) - \ sin \ left (x + \ dfrac (3 \ pi) (2) \ right) = 0 $.
b) Find all roots of this equation that belong to the interval $ \ left [\ dfrac (5 \ pi) (2); 4 \ pi \ right] $.

b) Find all the roots of this equation that belong to the interval $ \ left [\ log_5 2; \ log_5 20 \ right] $.

a) Solve the equation $ 8 \ sin ^ 2 x + 2 \ sqrt (3) \ cos \ left (\ dfrac (3 \ pi) (2) - x \ right) = 9 $.
b) Find all roots of this equation that belong to the interval $ \ left [- \ dfrac (5 \ pi) (2); - \ pi \ right] $.

a) Solve the equation $ 2 \ log_3 ^ 2 (2 \ cos x) - 5 \ log_3 (2 \ cos x) + 2 = 0 $.
b) Find all roots of this equation that belong to the interval $ \ left [\ pi; \ dfrac (5 \ pi) (2) \ right] $.

a) Solve the equation $ \ left (\ dfrac (1) (49) \ right) ^ (\ sin x) = 7 ^ (2 \ sin 2x) $.
b) Find all roots of this equation that belong to the interval $ \ left [\ dfrac (3 \ pi) (2); 3 \ pi \ right] $.

a) Solve the equation $ \ sin x + \ left (\ cos \ dfrac (x) (2) - \ sin \ dfrac (x) (2) \ right) \ left (\ cos \ dfrac (x) (2) + \ sin \ dfrac (x) (2) \ right) = 0 $.
b) Find all roots of this equation that belong to the interval $ \ left [\ pi; \ dfrac (5 \ pi) (2) \ right] $.

a) Solve the equation $ \ log_4 (\ sin x + \ sin 2x + 16) = 2 $.
b) Find all roots of this equation that belong to the interval $ \ left [-4 \ pi; - \ dfrac (5 \ pi) (2) \ right] $.

A selection of assignments from past years

a) Solve the equation $ \ dfrac (\ sin x) (\ sin ^ 2 \ dfrac (x) (2)) = 4 \ cos ^ 2 \ dfrac (x) (2) $.
b) Find all roots of this equation that belong to the segment $ \ left [- \ dfrac (9 \ pi) (2); -3 \ pi \ right] $. (USE-2018. Early wave)
a) Solve the equation $ \ sqrt (x ^ 3 - 4x ^ 2 - 10x + 29) = 3 - x $.
b) Find all the roots of this equation that belong to the segment $ \ left [- \ sqrt (3); \ sqrt (30) \ right] $. (USE-2018. Early wave, reserve day)
a) Solve the equation $ 2 \ sin ^ 2 x + \ sqrt2 \ sin \ left (x + \ dfrac (\ pi) (4) \ right) = \ cos x $.
b) Find all the roots of this equation that belong to the segment $ \ left [-2 \ pi; - \ dfrac (\ pi) (2) \ right] $. (USE-2018. Main wave)
a) Solve the equation $ \ sqrt6 \ sin ^ 2 x + \ cos x = 2 \ sin \ left (x + \ dfrac (\ pi) (6) \ right) $.
b) Find all the roots of this equation that belong to the segment $ \ left [3 \ pi; \ dfrac (9 \ pi) (2) \ right] $. (USE-2018. Main wave)
a) Solve the equation $ \ sin x + 2 \ sin \ left (2x + \ dfrac (\ pi) (6) \ right) = \ sqrt3 \ sin 2x + 1 $.
b) Find all roots of this equation that belong to the segment $ \ left [- \ dfrac (7 \ pi) (2); -2 \ pi \ right] $. (USE-2018. Main wave)
a) Solve the equation $ \ cos ^ 2 x + \ sin x = \ sqrt2 \ sin \ left (x + \ dfrac (\ pi) (4) \ right) $.
b) Find all the roots of this equation that belong to the segment $ \ left [-4 \ pi; - \ dfrac (5 \ pi) (2) \ right] $. (USE-2018. Main wave)
a) Solve the equation $ 2 \ sin \ left (2x + \ dfrac (\ pi) (3) \ right) - \ sqrt (3) \ sin x = \ sin 2x + \ sqrt3 $.
a) Solve the equation $ 2 \ sqrt3 \ sin \ left (x + \ dfrac (\ pi) (3) \ right) - \ cos 2x = 3 \ cos x - 1 $.
b) Find all roots of this equation that belong to the segment $ \ left [2 \ pi; \ dfrac (7 \ pi) (2) \ right] $. (USE-2018. Main wave)
a) Solve the equation $ 2 \ sin \ left (2x + \ dfrac (\ pi) (6) \ right) - \ cos x = \ sqrt3 \ sin 2x - 1 $.
b) Find all roots of this equation that belong to the segment $ \ left [\ dfrac (5 \ pi) (2); 4 \ pi \ right] $. (USE-2018. Main wave)
a) Solve the equation $ \ sqrt2 \ sin \ left (\ dfrac (\ pi) (4) + x \ right) + \ cos 2x = \ sin x - 1 $.
b) Find all roots of this equation that belong to the segment $ \ left [\ dfrac (7 \ pi) (2); 5 \ pi \ right] $. (USE-2018. Main wave)
a) Solve the equation $ \ sqrt2 \ sin \ left (2x + \ dfrac (\ pi) (4) \ right) + \ sqrt2 \ cos x = \ sin 2x - 1 $.
b) Find all roots of this equation that belong to the segment $ \ left [- \ dfrac (5 \ pi) (2); - \ pi \ right] $. (USE-2018. Main wave)
a) Solve the equation $ 2 \ sin \ left (x + \ dfrac (\ pi) (3) \ right) + \ cos 2x = \ sqrt3 \ cos x + 1 $.
b) Find all the roots of this equation that belong to the segment $ \ left [-3 \ pi; - \ dfrac (3 \ pi) (2) \ right] $. (USE-2018. Main wave)
b) Find all the roots of this equation that belong to the segment $ \ left [\ pi; \ dfrac (5 \ pi) (2) \ right] $. (USE-2018. Main wave)
a) Solve the equation $ 2 \ sin \ left (x + \ dfrac (\ pi) (4) \ right) + \ cos 2x = \ sqrt2 \ cos x + 1 $.
b) Find all the roots of this equation that belong to the segment $ \ left [\ pi; \ dfrac (5 \ pi) (2) \ right] $. (USE-2018. Main wave, reserve day)
a) Solve the equation $ 2 \ cos x - \ sqrt3 \ sin ^ 2 x = 2 \ cos ^ 3 x $.
b) Find all roots of this equation that belong to the segment $ \ left [- \ dfrac (7 \ pi) (2); -2 \ pi \ right] $. (USE-2018. Main wave, reserve day)
a) Solve the equation $ 2 \ cos x + \ sin ^ 2 x = 2 \ cos ^ 3 x $.
b) Find all roots of this equation that belong to the segment $ \ left [- \ dfrac (9 \ pi) (2); -3 \ pi \ right] $. (USE-2018. Main wave, reserve day)
a) Solve the equation $ 2 \ sqrt2 \ sin \ left (x + \ dfrac (\ pi) (3) \ right) + 2 \ cos ^ 2 x = 2 + \ sqrt6 \ cos x $.
b) Find all the roots of this equation that belong to the segment $ \ left [-3 \ pi; - \ dfrac (3 \ pi) (2) \ right] $. (USE-2018. Main wave, reserve day)
a) Solve the equation $ x - 3 \ sqrt (x - 1) + 1 = 0 $.
b) Find all the roots of this equation that belong to the segment $ \ left [\ sqrt (3); \ sqrt (20) \ right] $. (USE-2018. Main wave, reserve day)
a) Solve the equation $ 2x \ cos x - 8 \ cos x + x - 4 = 0 $.
b) Indicate the roots of this equation that belong to the segment $ \ left [- \ dfrac (\ pi) (2); \ \ pi \ right] $. (USE-2017, main wave, reserve day)
a) Solve the equation $ \ log_3 (x ^ 2 - 2x) = 1 $.
b) Indicate the roots of this equation that belong to the segment $ \ left [\ log_2 0 (,) 2; \ \ log_2 5 \ right] $. (USE-2017, main wave, reserve day)
a) Solve the equation $ \ log_3 (x ^ 2 - 24x) = 4 $.
b) Indicate the roots of this equation that belong to the segment $ \ left [\ log_2 0 (,) 1; \ 12 \ sqrt (5) \ right] $. (USE-2017, main wave, reserve day)
a) Solve the equation $ 0 (,) 4 ^ (\ sin x) + 2 (,) 5 ^ (\ sin x) = 2 $.
b) Indicate the roots of this equation that belong to the segment $ \ left [2 \ pi; \ \ dfrac (7 \ pi) (2) \ right] $. (USE-2017, main wave)
a) Solve the equation $ \ log_8 \ left (7 \ sqrt (3) \ sin x - \ cos 2x - 10 \ right) = 0 $.
b) Indicate the roots of this equation that belong to the segment $ \ left [\ dfrac (3 \ pi) (2); \ 3 \ pi \ right] $. (USE-2017, main wave)
a) Solve the equation $ \ log_4 \ left (2 ^ (2x) - \ sqrt (3) \ cos x - 6 \ sin ^ 2 x \ right) = x $.
b) Indicate the roots of this equation that belong to the segment $ \ left [\ dfrac (5 \ pi) (2); \ 4 \ pi \ right] $. (USE-2017, main wave)
a) Solve the equation $ 2 \ log_2 ^ 2 \ left (\ sin x \ right) - 5 \ log_2 \ left (\ sin x \ right) - 3 = 0 $.
b) Indicate the roots of this equation that belong to the segment $ \ left [- 3 \ pi; \ - \ dfrac (3 \ pi) (2) \ right] $. (USE-2017, main wave)
a) Solve the equation $ 81 ^ (\ cos x) - 12 \ cdot 9 ^ (\ cos x) + 27 = 0 $.
b) Indicate the roots of this equation that belong to the segment $ \ left [- 4 \ pi; \ - \ dfrac (5 \ pi) (2) \ right] $. (USE-2017, main wave)
a) Solve the equation $ 8 ^ x - 9 \ cdot 2 ^ (x + 1) + 2 ^ (5 - x) = 0 $.
b) Indicate the roots of this equation that belong to the segment $ \ left [\ log_5 2; \ \ log_5 20 \ right] $. (USE-2017, early wave)
a) Solve the equation $ 2 \ log ^ 2_9 x - 3 \ log_9 x + 1 = 0 $.
b) Indicate the roots of this equation that belong to the segment $ \ left [\ sqrt (10); \ \ sqrt (99) \ right] $. (USE-2016, main wave, reserve day)
a) Solve the equation $ 6 \ log ^ 2_8 x - 5 \ log_8 x + 1 = 0 $.
b) Indicate the roots of this equation that belong to the segment $ \ left [2; \ 2 (,) 5 \ right] $. (USE-2016, main wave, reserve day)
a) Solve the equation $ \ sin 2x = 2 \ sin x + \ sin \ left (x + \ dfrac (3 \ pi) (2) \ right) + 1 $.
b) Indicate the roots of this equation that belong to the segment $ \ left [-4 \ pi; \ - \ dfrac (5 \ pi) (2) \ right] $. (USE-2016, main wave, reserve day)
a) Solve the equation $ 2 \ cos ^ 2 x + 1 = 2 \ sqrt (2) \ cos \ left (\ dfrac (3 \ pi) (2) - x \ right) $.
b) Indicate the roots of this equation that belong to the segment $ \ left [\ dfrac (3 \ pi) (2); \ 3 \ pi \ right] $. (USE-2016, main wave)
a) Solve the equation $ 2 \ log ^ 2_2 (2 \ cos x) - 9 \ log_2 (2 \ cos x) + 4 = 0 $.
b) Indicate the roots of this equation that belong to the segment $ \ left [-2 \ pi; \ - \ dfrac (\ pi) (2) \ right] $. (USE-2016, main wave)
a) Solve the equation $ 8 ^ x - 7 \ cdot 4 ^ x - 2 ^ (x + 4) + 112 = 0 $.
b) Indicate the roots of this equation that belong to the segment $ \ left [\ log_2 5; \ \ log_2 11 \ right] $. (USE-2016, early wave)
a) Solve the equation $ \ cos 2x + \ cos ^ 2 \ left (\ dfrac (3 \ pi) (2) - x \ right) = 0.25 $.
b) Indicate the roots of this equation that belong to the segment $ \ left [-4 \ pi; \ - \ dfrac (5 \ pi) (2) \ right] $. (USE-2016, early wave)
a) Solve the equation $ \ dfrac (13 \ sin ^ 2 x - 5 \ sin x) (13 \ cos x + 12) = 0 $.
b) Indicate the roots of this equation that belong to the segment $ \ left [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ right] $. (USE-2016, early wave)
a) Solve the equation $ \ dfrac (\ sin2x) (\ sin \ left (\ dfrac (7 \ pi) (2) - x \ right)) = \ sqrt (2) $.
b) Indicate the roots of this equation that belong to the segment $ \ left $. (USE-2015, main wave)
a) Solve the equation $ 4 \ sin ^ 2 x = \ mathrm (tg) x $.
b) Indicate the roots of this equation that belong to the segment $ \ left [- \ pi; \ 0 \ right] $. (USE-2015, main wave)
a) Solve the equation $ 3 \ cos 2x - 5 \ sin x + 1 = 0 $.
b) Indicate the roots of this equation that belong to the segment $ \ left [\ pi; \ \ dfrac (5 \ pi) (2) \ right] $. (USE-2015, main wave)
a) Solve the equation $ \ cos 2x - 5 \ sqrt (2) \ cos x - 5 = 0 $.
b) Indicate the roots of this equation that belong to the segment $ \ left [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ right] $. (USE-2015, main wave)
a) Solve the equation $ \ sin 2x + \ sqrt (2) \ sin x = 2 \ cos x + \ sqrt (2) $.
b) Indicate the roots of this equation that belong to the segment $ \ left [\ pi; \ \ dfrac (5 \ pi) (2) \ right] $. (USE-2015, early wave)
a) Solve the equation $ 2 \ cos ^ 3 x - \ cos ^ 2 x + 2 \ cos x - 1 = 0 $.
b) Indicate the roots of this equation that belong to the segment $ \ left [2 \ pi; \ \ dfrac (7 \ pi) (2) \ right] $. (USE-2015, early wave)
a) Solve the equation $ \ mathrm (tg) ^ 2 x + (1 + \ sqrt (3)) \ mathrm (tg) x + \ sqrt (3) = 0 $.
b) Indicate the roots of this equation that belong to the segment $ \ left [\ dfrac (5 \ pi) (2); \ 4 \ pi \ right] $. (USE-2014, main wave)
a) Solve the equation $ 2 \ sqrt (3) \ cos ^ 2 \ left (\ dfrac (3 \ pi) (2) + x \ right) - \ sin 2x = 0 $.
b) Indicate the roots of this equation that belong to the segment $ \ left [\ dfrac (3 \ pi) (2); \ 3 \ pi \ right] $. (USE-2014, main wave)
a) Solve the equation $ \ cos 2x + \ sqrt (2) \ sin \ left (\ dfrac (\ pi) (2) + x \ right) + 1 = 0 $.
b) Indicate the roots of this equation that belong to the segment $ \ left [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ right] $. (USE-2014, main wave)
a) Solve the equation $ - \ sqrt (2) \ sin \ left (- \ dfrac (5 \ pi) (2) + x \ right) \ cdot \ sin x = \ cos x $.
b) Indicate the roots of this equation that belong to the segment $ \ left [\ dfrac (9 \ pi) (2); \ 6 \ pi \ right] $. (USE-2014, early wave)
a) Solve the equation $ \ sin 2x = \ sin \ left (\ dfrac (\ pi) (2) + x \ right) $.
b) Indicate the roots of this equation that belong to the segment $ \ left [- \ dfrac (7 \ pi) (2); \ - \ dfrac (5 \ pi) (2) \ right] $. (USE-2013, main wave)
a) Solve the equation $ 6 \ sin ^ 2 x + 5 \ sin \ left (\ dfrac (\ pi) (2) - x \ right) - 2 = 0 $.
b) Indicate the roots of this equation that belong to the segment $ \ left [-5 \ pi; \ - \ dfrac (7 \ pi) (2) \ right] $. (USE-2012, second wave)

The purpose of the lesson:

a) to consolidate the ability to solve the simplest trigonometric equations;

b) teach to choose the roots of trigonometric equations from a given interval

During the classes.

1. Actualization of knowledge.

a) Checking homework: the class was given an anticipatory homework - to solve the equation and find a way to select roots from a given interval.

1) cos x= -0.5, where xI [-]. Answer:.

2) sin x=, where xI. Answer: ; ...

3) cos 2 x= -, where хI. Answer:

Pupils write down the solution on the board, someone using a graph, someone using a selection method.

At this time the class works orally.

Find the meaning of the expression:

a) tg - sin + cos + sin. Answer: 1.

b) 2arccos 0 + 3 arccos 1. Answer: ?

c) arcsin + arcsin. Answer:.

d) 5 arctan (-) - arccos (-). Answer:-.

- Let's check your homework, open your homework notebooks.

Some of you have found a solution by a fit method, and some by a graph.

2. Conclusion on how to solve these tasks and the problem statement, ie, the message of the topic and the purpose of the lesson.

- a) It is difficult to solve with the help of selection if a large interval is given.

- b) The graphical method does not give accurate results, requires verification, and takes a lot of time.

- Therefore, there must be at least one more method, the most universal - let's try to find it. So what are we going to do in class today? (Learn to choose the roots of a trigonometric equation at a given interval.)

- Example 1 (The student goes to the blackboard)

cos x= -0.5, where xI [-].

Question: What does the answer to this task depend on? (From the general solution of the equation. Let us write the solution in general form). The decision is written on the board

х = + 2? k, where k R.

- Let's write this solution in the form of a set:

- What do you think, for what record of the solution is it convenient to choose roots in the interval? (from the second entry). But this is again a selection method. What do we need to know to get the right answer? (You need to know the values of k).

(Let's make a mathematical model to find k).



since kI Z, then k = 0, hence X= =	this inequality shows that there are no integer values of k.

Conclusion: To select roots from a given interval when solving a trigonometric equation, you need to:

to solve an equation of the form sin x = a, cos x = a it is more convenient to write the roots of the equation as two series of roots.
to solve equations of the form tg x = a, ctg x = a write down the general formula for the roots.
draw up a mathematical model for each solution in the form of a double inequality and find the integer value of the parameter k or n.
substitute these values into the root formula and calculate them.

3. Anchoring.

Solve examples 2 and 3 from homework using the obtained algorithm. At the same time, two students work at the blackboard, followed by checking the work.

In this article I will try to explain 2 ways selection of roots in trigonometric equation: using inequalities and using the trigonometric circle. Let's go straight to an illustrative example and deal with the case.

A) Solve the equation sqrt (2) cos ^ 2x = sin (Pi / 2 + x)
b) Find all roots of this equation belonging to the interval [-7Pi / 2; -2Pi]

Let's solve point a.

We use the reduction formula for the sine sin (Pi / 2 + x) = cos (x)

Sqrt (2) cos ^ 2x = cosx

Sqrt (2) cos ^ 2x - cosx = 0

Cosx (sqrt (2) cosx - 1) = 0

X1 = Pi / 2 + Pin, n ∈ Z

Sqrt (2) cosx - 1 = 0

Cosx = 1 / sqrt (2)

Cosx = sqrt (2) / 2

X2 = arccos (sqrt (2) / 2) + 2Pin, n ∈ Z
x3 = -arccos (sqrt (2) / 2) + 2Pin, n ∈ Z

X2 = Pi / 4 + 2Pin, n ∈ Z
x3 = -Pi / 4 + 2Pin, n ∈ Z

Let's solve point b.

1) Selection of roots using inequalities

Here everything is done simply, we substitute the obtained roots in the given interval [-7Pi / 2; -2Pi], find integer values for n.

7Pi / 2 less than or equal to Pi / 2 + Pin less than or equal to -2Pi

Divide everything into Pi at once

7/2 is less than or equal to 1/2 + n is less than or equal to -2

7/2 - 1/2 less than or equal to n less than or equal to -2 - 1/2

4 less than or equal to n less than or equal to -5/2

The integer n in this range is -4 and -3. So the roots belonging to this interval will be Pi / 2 + Pi (-4) = -7Pi / 2, Pi / 2 + Pi (-3) = -5Pi / 2

Similarly, we make two more inequalities

7Pi / 2 less than or equal to Pi / 4 + 2Pin less than or equal to -2Pi
-15/8 less than or equal to n less than or equal to -9/8

There are no integer n in this interval

7Pi / 2 less than or equal to -Pi / 4 + 2Pin less than or equal to -2Pi
-13/8 less than or equal to n less than or equal to -7/8

One integer n in this span is -1. So the selected root on this interval is -Pi / 4 + 2Pi * (- 1) = -9Pi / 4.

So the answer in point b: -7Pi / 2, -5Pi / 2, -9Pi / 4

2) Selecting roots using a trigonometric circle

To use this method, you need to understand how this circle works. I will try to explain in simple language how I understand this. I think in schools in algebra lessons this topic was explained many times by the clever words of the teacher, complex formulations in textbooks. Personally, I understand this as a circle that can be traversed an infinite number of times, due to the fact that the sine and cosine functions are periodic.

Let's go counterclockwise once

Let's go around 2 times counterclockwise

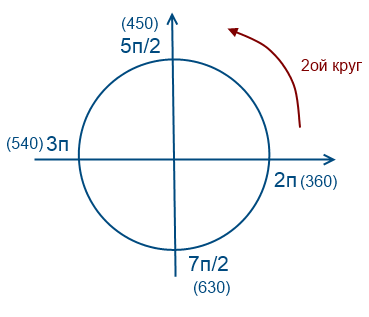
Let's go around 1 time clockwise (the values will be negative)

Let's get back to our question, we need to select roots in the interval [-7Pi / 2; -2Pi]

To get to the numbers -7Pi / 2 and -2Pi, you need to go around the circle counterclockwise two times. In order to find the roots of the equation on this interval, it is necessary to estimate and substitute.

Consider x = Pi / 2 + Pin. What is the approximate value of n for the value of x to be somewhere in this interval? Substituting, say -2, we get Pi / 2 - 2Pi = -3Pi / 2, obviously this is not included in our interval, so we take less than -3, Pi / 2 - 3Pi = -5Pi / 2, it fits, let's try -4 again , Pi / 2 - 4Pi = -7Pi / 2 is also suitable.

Reasoning similarly for Pi / 4 + 2Pin and -Pi / 4 + 2Pin, we find another root -9Pi / 4.

Comparison of the two methods.

The first method (using inequalities) is much more reliable and much easier to understand, but if you really seriously deal with the trigonometric circle and the second selection method, then the selection of roots will be much faster, you can save about 15 minutes on the exam.

a) Solve the equation:.

b) Find all the roots of this equation that belong to the segment.

The solution of the problem

This lesson considers an example of solving a trigonometric equation, which can be used as an example for solving problems of type C1 in preparation for the exam in mathematics.

First of all, the scope of the function is determined - all the allowed values of the argument. Then, during the solution, the trigonometric sine function is converted to cosine using the reduction formula. Further, all the terms of the equation are transferred to its left side, where the common factor is taken out of the brackets. Each factor is set equal to zero, which allows you to determine the roots of the equation. Then the roots belonging to the given segment are determined by the method of turns. To do this, a loop is marked on the constructed unit circle from the left boundary of the specified segment to the right. Further, the found roots on the unit circle are connected by segments with its center and the points at which these segments intersect the loop are determined. These intersection points are the desired answer to the second part of the problem.