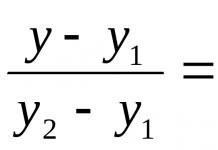Sections: Mathematics

Class: 11

Lesson 1

Topic: Grade 11 (preparation for the exam)

Simplification of trigonometric expressions.

Solving the simplest trigonometric equations. (2 hours)

Goals:

• To systematize, generalize, expand the knowledge and skills of students related to the application of trigonometry formulas and the solution of the simplest trigonometric equations.

Equipment for the lesson:

Lesson structure:

1. Organizational moment
2. Testing on laptops. The discussion of the results.
3. Simplifying trigonometric expressions
4. Solving the simplest trigonometric equations
5. Independent work.
6. Lesson summary. Explanation of the home assignment.

1. Organizational moment. (2 minutes.)

The teacher greets the audience, announces the topic of the lesson, reminds of the previous assignment to repeat trigonometry formulas, and sets up students for testing.

2. Testing. (15min + 3min discussion)

The goal is to test the knowledge of trigonometric formulas and the ability to apply them. Each student has a laptop on the desk with a test version.

There can be as many options as you like, I will give an example of one of them:

Option I.

Simplify expressions:

a) basic trigonometric identities

1.sin 2 3y + cos 2 3y + 1;

b) addition formulas

3.sin5x - sin3x;

c) converting the product into a sum

6.2sin8y cozy;

d) double angle formulas

7.2sin5x cos5x;

e) half angle formulas

f) triple angle formulas

g) universal substitution

h) lowering the degree

16.cos 2 (3x / 7);

Students on a laptop see their answers in front of each formula.

The work is instantly checked by the computer. The results are displayed on a large screen for all to see.

Also, after the end of the work, the correct answers are shown on the students' laptops. Each student sees where the mistake was made and what formulas he needs to repeat.

3. Simplification of trigonometric expressions. (25 min.)

The goal is to review, practice and consolidate the application of the basic trigonometry formulas. Solving problems B7 from the exam.

At this stage, it is advisable to divide the class into groups of strong (work independently with subsequent verification) and weak students who work with the teacher.

Assignment for strong learners (prepared in advance on a printed basis). The main emphasis is placed on the formulas of reduction and double angle, according to the USE 2011.

Simplify expressions (for strong learners):

In parallel, the teacher works with weak students, discussing and solving tasks on the screen under the dictation of the students.

Calculate:

5) sin (270º - α) + cos (270º + α)

6)

Simplify:

It was the turn of the discussion of the results of the work of the strong group.

Answers appear on the screen, and also, with the help of a video camera, the works of 5 different students are displayed (one task for each).

The weak group sees the condition and method of solution. Discussion and analysis are in progress. With the use of technical means, this happens quickly.

4. Solution of the simplest trigonometric equations. (30 minutes.)

The goal is to repeat, systematize and generalize the solution of the simplest trigonometric equations, recording their roots. Solution to problem B3.

Any trigonometric equation, no matter how we solve it, leads to the simplest one.

When completing the assignment, students should be drawn to the recording of the roots of the equations of particular cases and the general form and to the selection of the roots in the last equation.

Solve equations:

Write down the smallest positive root in response.

5. Independent work (10 min.)

The goal is to test the acquired skills, identify problems, errors and ways to eliminate them.

Different-level work is offered at the choice of the student.

Option for "3"

1) Find the value of an expression

2) Simplify the expression 1 - sin 2 3α - cos 2 3α

3) Solve the equation

Option for "4"

1) Find the value of an expression

2) Solve the equation Write down the smallest positive root in the answer.

Option for "5"

1) Find tgα if

2) Find the root of the equation Write down the smallest positive root in your answer.

6. Lesson summary (5 min.)

The teacher sums up the fact that in the lesson the trigonometric formulas were repeated and fixed, the solution of the simplest trigonometric equations.

Homework assignment (prepared on a printed basis in advance) with spot checks in the next lesson.

Solve equations:

9)

10) Indicate the smallest positive root in your answer.

Session 2

Topic: Grade 11 (preparation for the exam)

Methods for solving trigonometric equations. Selection of roots. (2 hours)

Goals:

• To generalize and systematize knowledge on solving trigonometric equations of various types.
• To promote the development of students' mathematical thinking, the ability to observe, compare, generalize, classify.
• Encourage students to overcome difficulties in the process of mental activity, to self-control, introspection of their activities.

Equipment for the lesson: KRMu, laptops for each student.

Lesson structure:

1. Organizational moment
2. Discussion d / h and samot. works of the last lesson
3. Repetition of methods for solving trigonometric equations.
4. Solving trigonometric equations
5. Selection of roots in trigonometric equations.
6. Independent work.
7. Lesson summary. Homework.

1. Organizational moment (2 min.)

The teacher greets the audience, announces the topic of the lesson and the work plan.

2. a) Review of homework (5 min.)

The goal is to check execution. One work with the help of a video camera is displayed on the screen, the rest are selectively collected for the teacher's check.

b) Analysis of independent work (3 min.)

The goal is to analyze the mistakes, indicate the ways to overcome them.

On the screen, answers and solutions, students have their work pre-assigned. Analysis is progressing quickly.

3. Repetition of methods for solving trigonometric equations (5 min.)

The goal is to recall the methods for solving trigonometric equations.

Ask students what methods they know for solving trigonometric equations. Emphasize that there are so-called basic (frequently used) methods:

• variable replacement,
• factorization,
• homogeneous equations,

and there are applied methods:

• according to the formulas for converting a sum into a product and a product into a sum,
• by the degree reduction formulas,
• universal trigonometric substitution
• introduction of an auxiliary angle,
• multiplication by some trigonometric function.

It should also be remembered that one equation can be solved in different ways.

4. Solving trigonometric equations (30 min.)

The goal is to generalize and consolidate knowledge and skills on this topic, to prepare for the decision of C1 from the exam.

I consider it expedient to solve the equations for each method together with the students.

The student dictates the decision, the teacher writes it down on the tablet, the whole process is displayed on the screen. This will allow you to quickly and efficiently recall the previously covered material.

Solve equations:

1) change of variable 6cos 2 x + 5sinx - 7 = 0

2) factoring 3cos (x / 3) + 4cos 2 (x / 3) = 0

3) homogeneous equations sin 2 x + 3cos 2 x - 2sin2x = 0

4) converting the sum to the product cos5x + cos7x = cos (π + 6x)

5) converting the product to the sum 2sinx sin2x + cos3x = 0

6) lowering the power sin2x - sin 2 2x + sin 2 3x = 0.5

7) universal trigonometric substitution sinx + 5cosx + 5 = 0.

Solving this equation, it should be noted that the use of this method leads to a narrowing of the domain of definition, since the sine and cosine are replaced by tg (x / 2). Therefore, before writing out the answer, you need to check whether the numbers from the set π + 2πn, n Z are horses of this equation.

8) introduction of an auxiliary angle √3sinx + cosx - √2 = 0

9) multiplication by some trigonometric function cosx cos2x cos4x = 1/8.

5. Selection of roots of trigonometric equations (20 min.)

Since in conditions of fierce competition when entering universities, solving one first part of the exam is not enough, most students should pay attention to the tasks of the second part (C1, C2, C3).

Therefore, the purpose of this stage of the lesson is to recall the previously studied material, to prepare for solving the C1 problem from the Unified State Examination in 2011.

There are trigonometric equations in which you need to select roots when writing out an answer. This is due to some restrictions, for example: the denominator of the fraction is not zero, the expression under the even root is non-negative, the expression under the sign of the logarithm is positive, etc.

Such equations are considered equations of increased complexity and in the version of the exam are in the second part, namely C1.

Solve the equation:

The fraction is zero if then using the unit circle, we select the roots (see Figure 1)

Picture 1.

we get x = π + 2πn, n Z

Answer: π + 2πn, n Z

On the screen, the selection of roots is shown on a circle in a color image.

The product is equal to zero when at least one of the factors is equal to zero, and the arc, in this case, does not lose its meaning. Then

Select the roots using the unit circle (see Figure 2)

V identical transformations trigonometric expressions the following algebraic techniques can be used: addition and subtraction of the same terms; taking the common factor out of the parentheses; multiplication and division by the same amount; application of abbreviated multiplication formulas; selection of a full square; factorization of a square trinomial; introduction of new variables in order to simplify transformations.

When converting trigonometric expressions containing fractions, you can use the properties of proportion, reduction of fractions, or converting fractions to a common denominator. In addition, you can use the selection of the integer part of the fraction, multiplying the numerator and denominator of the fraction by the same amount, as well as, if possible, take into account the homogeneity of the numerator or denominator. If necessary, you can represent a fraction as the sum or difference of several simpler fractions.

In addition, when applying all the necessary methods for converting trigonometric expressions, it is necessary to constantly take into account the range of permissible values ​​of the converted expressions.

Let's look at a few examples.

Example 1.

Calculate А = (sin (2x - π) cos (3π - x) + sin (2x - 9π / 2) cos (x + π / 2)) 2 + (cos (x - π / 2) cos ( 2x - 7π / 2) +
+ sin (3π / 2 - x) sin (2x -5π / 2)) 2

Solution.

It follows from the reduction formulas:

sin (2x - π) = -sin 2x; cos (3π - x) = -cos x;

sin (2x - 9π / 2) = -cos 2x; cos (x + π / 2) = -sin x;

cos (x - π / 2) = sin x; cos (2x - 7π / 2) = -sin 2x;

sin (3π / 2 - x) = -cos x; sin (2x - 5π / 2) = -cos 2x.

Whence, by virtue of the formulas for the addition of arguments and the basic trigonometric identity, we obtain

A = (sin 2x cos x + cos 2x sin x) 2 + (-sin x sin 2x + cos x cos 2x) 2 = sin 2 (2x + x) + cos 2 (x + 2x) =
= sin 2 3x + cos 2 3x = 1

Answer: 1.

Example 2.

Convert the expression М = cos α + cos (α + β) cos γ + cos β - sin (α + β) sin γ + cos γ into a product.

Solution.

From the formulas for the addition of arguments and the formulas for the transformation of the sum of trigonometric functions into a product after the corresponding grouping, we have

М = (cos (α + β) cos γ - sin (α + β) sin γ) + cos α + (cos β + cos γ) =

2cos ((β + γ) / 2) cos ((β - γ) / 2) + (cos α + cos (α + β + γ)) =

2cos ((β + γ) / 2) cos ((β - γ) / 2) + 2cos (α + (β + γ) / 2) cos ((β + γ) / 2)) =

2cos ((β + γ) / 2) (cos ((β - γ) / 2) + cos (α + (β + γ) / 2)) =

2cos ((β + γ) / 2) 2cos ((β - γ) / 2 + α + (β + γ) / 2) / 2) cos ((β - γ) / 2) - (α + ( β + γ) / 2) / 2) =

4cos ((β + γ) / 2) cos ((α + β) / 2) cos ((α + γ) / 2).

Answer: М = 4cos ((α + β) / 2) cos ((α + γ) / 2) cos ((β + γ) / 2).

Example 3.

Show that the expression A = cos 2 (x + π / 6) - cos (x + π / 6) cos (x - π / 6) + cos 2 (x - π / 6) takes one and the same meaning. Find this value.

Solution.

Here are two ways to solve this problem. Applying the first method, by selecting a complete square and using the corresponding basic trigonometric formulas, we get

А = (cos (x + π / 6) - cos (x - π / 6)) 2 + cos (x - π / 6) cos (x - π / 6) =

4sin 2 x sin 2 π / 6 + 1/2 (cos 2x + cos π / 3) =

Sin 2 x + 1/2 cos 2x + 1/4 = 1/2 (1 - cos 2x) + 1/2 cos 2x + 1/4 = 3/4.

Solving the problem in the second way, consider A as a function of x from R and calculate its derivative. After transformations we get

А´ = -2cos (x + π / 6) sin (x + π / 6) + (sin (x + π / 6) cos (x - π / 6) + cos (x + π / 6) sin (x + π / 6)) - 2cos (x - π / 6) sin (x - π / 6) =

Sin 2 (x + π / 6) + sin ((x + π / 6) + (x - π / 6)) - sin 2 (x - π / 6) =

Sin 2x - (sin (2x + π / 3) + sin (2x - π / 3)) =

Sin 2x - 2sin 2xcos π / 3 = sin 2x - sin 2x ≡ 0.

Hence, by virtue of the criterion of constancy of a function differentiable on an interval, we conclude that

A (x) ≡ (0) = cos 2 π / 6 - cos 2 π / 6 + cos 2 π / 6 = (√3 / 2) 2 = 3/4, x € R.

Answer: A = 3/4 for x € R.

The main methods of proving trigonometric identities are:

a) reduction of the left side of the identity to the right by appropriate transformations;
b) reduction of the right side of the identity to the left;
v) reduction of the right and left sides of the identity to the same kind;
G) reduction to zero of the difference between the left and right sides of the identity being proved.

Example 4.

Check that cos 3x = -4cos x cos (x + π / 3) cos (x + 2π / 3).

Solution.

Transforming the right-hand side of this identity according to the corresponding trigonometric formulas, we have

4cos x cos (x + π / 3) cos (x + 2π / 3) =

2cos x (cos ((x + π / 3) + (x + 2π / 3)) + cos ((x + π / 3) - (x + 2π / 3))) =

2cos x (cos (2x + π) + cos π / 3) =

2cos x cos 2x - cos x = (cos 3x + cos x) - cos x = cos 3x.

The right side of the identity has been reduced to the left.

Example 5.

Prove that sin 2 α + sin 2 β + sin 2 γ - 2cos α cos β cos γ = 2 if α, β, γ are interior angles of some triangle.

Solution.

Taking into account that α, β, γ are interior angles of some triangle, we obtain that

α + β + γ = π and, therefore, γ = π - α - β.

sin 2 α + sin 2 β + sin 2 γ - 2cos α cos β cos γ =

Sin 2 α + sin 2 β + sin 2 (π - α - β) - 2cos α cos β cos (π - α - β) =

Sin 2 α + sin 2 β + sin 2 (α + β) + (cos (α + β) + cos (α - β) (cos (α + β) =

Sin 2 α + sin 2 β + (sin 2 (α + β) + cos 2 (α + β)) + cos (α - β) (cos (α + β) =

1/2 · (1 - cos 2α) + ½ · (1 - cos 2β) + 1 + 1/2 · (cos 2α + cos 2β) = 2.

The original equality is proved.

Example 6.

To prove that for one of the angles α, β, γ of the triangle to be equal to 60 °, it is necessary and sufficient that sin 3α + sin 3β + sin 3γ = 0.

Solution.

The condition of this problem presupposes proof of both necessity and sufficiency.

First, let us prove need.

It can be shown that

sin 3α + sin 3β + sin 3γ = -4cos (3α / 2) cos (3β / 2) cos (3γ / 2).

Hence, taking into account that cos (3/2 60 °) = cos 90 ° = 0, we obtain that if one of the angles α, β or γ is equal to 60 °, then

cos (3α / 2) cos (3β / 2) cos (3γ / 2) = 0 and, therefore, sin 3α + sin 3β + sin 3γ = 0.

Let us now prove adequacy the specified condition.

If sin 3α + sin 3β + sin 3γ = 0, then cos (3α / 2) cos (3β / 2) cos (3γ / 2) = 0, and therefore

either cos (3α / 2) = 0, or cos (3β / 2) = 0, or cos (3γ / 2) = 0.

Hence,

or 3α / 2 = π / 2 + πk, i.e. α = π / 3 + 2πk / 3,

or 3β / 2 = π / 2 + πk, i.e. β = π / 3 + 2πk / 3,

or 3γ / 2 = π / 2 + πk,

those. γ = π / 3 + 2πk / 3, where k ϵ Z.

Since α, β, γ are the angles of the triangle, we have

0 < α < π, 0 < β < π, 0 < γ < π.

Therefore, for α = π / 3 + 2πk / 3 or β = π / 3 + 2πk / 3 or

γ = π / 3 + 2πk / 3 of all kϵZ only k = 0 fits.

Whence it follows that either α = π / 3 = 60 °, or β = π / 3 = 60 °, or γ = π / 3 = 60 °.

The statement is proven.

Still have questions? Not sure how to simplify trigonometric expressions?
To get help from a tutor - register.
The first lesson is free!

site, with full or partial copying of the material, a link to the source is required.

Sections: Mathematics

Class: 11

Lesson 1

Topic: Grade 11 (preparation for the exam)

Simplification of trigonometric expressions.

Solving the simplest trigonometric equations. (2 hours)

Goals:

• To systematize, generalize, expand the knowledge and skills of students related to the application of trigonometry formulas and the solution of the simplest trigonometric equations.

Equipment for the lesson:

Lesson structure:

1. Organizational moment
2. Testing on laptops. The discussion of the results.
3. Simplifying trigonometric expressions
4. Solving the simplest trigonometric equations
5. Independent work.
6. Lesson summary. Explanation of the home assignment.

1. Organizational moment. (2 minutes.)

The teacher greets the audience, announces the topic of the lesson, reminds of the previous assignment to repeat trigonometry formulas, and sets up students for testing.

2. Testing. (15min + 3min discussion)

The goal is to test the knowledge of trigonometric formulas and the ability to apply them. Each student has a laptop on the desk with a test version.

There can be as many options as you like, I will give an example of one of them:

Option I.

Simplify expressions:

a) basic trigonometric identities

1.sin 2 3y + cos 2 3y + 1;

b) addition formulas

3.sin5x - sin3x;

c) converting the product into a sum

6.2sin8y cozy;

d) double angle formulas

7.2sin5x cos5x;

e) half angle formulas

f) triple angle formulas

g) universal substitution

h) lowering the degree

16.cos 2 (3x / 7);

Students on a laptop see their answers in front of each formula.

The work is instantly checked by the computer. The results are displayed on a large screen for all to see.

Also, after the end of the work, the correct answers are shown on the students' laptops. Each student sees where the mistake was made and what formulas he needs to repeat.

3. Simplification of trigonometric expressions. (25 min.)

The goal is to review, practice and consolidate the application of the basic trigonometry formulas. Solving problems B7 from the exam.

At this stage, it is advisable to divide the class into groups of strong (work independently with subsequent verification) and weak students who work with the teacher.

Assignment for strong learners (prepared in advance on a printed basis). The main emphasis is placed on the formulas of reduction and double angle, according to the USE 2011.

Simplify expressions (for strong learners):

In parallel, the teacher works with weak students, discussing and solving tasks on the screen under the dictation of the students.

Calculate:

5) sin (270º - α) + cos (270º + α)

6)

Simplify:

It was the turn of the discussion of the results of the work of the strong group.

Answers appear on the screen, and also, with the help of a video camera, the works of 5 different students are displayed (one task for each).

The weak group sees the condition and method of solution. Discussion and analysis are in progress. With the use of technical means, this happens quickly.

4. Solution of the simplest trigonometric equations. (30 minutes.)

The goal is to repeat, systematize and generalize the solution of the simplest trigonometric equations, recording their roots. Solution to problem B3.

Any trigonometric equation, no matter how we solve it, leads to the simplest one.

When completing the assignment, students should be drawn to the recording of the roots of the equations of particular cases and the general form and to the selection of the roots in the last equation.

Solve equations:

Write down the smallest positive root in response.

5. Independent work (10 min.)

The goal is to test the acquired skills, identify problems, errors and ways to eliminate them.

Different-level work is offered at the choice of the student.

Option for "3"

1) Find the value of an expression

2) Simplify the expression 1 - sin 2 3α - cos 2 3α

3) Solve the equation

Option for "4"

1) Find the value of an expression

2) Solve the equation Write down the smallest positive root in the answer.

Option for "5"

1) Find tgα if

2) Find the root of the equation Write down the smallest positive root in your answer.

6. Lesson summary (5 min.)

The teacher sums up the fact that in the lesson the trigonometric formulas were repeated and fixed, the solution of the simplest trigonometric equations.

Homework assignment (prepared on a printed basis in advance) with spot checks in the next lesson.

Solve equations:

9)

10) Indicate the smallest positive root in your answer.

Session 2

Topic: Grade 11 (preparation for the exam)

Methods for solving trigonometric equations. Selection of roots. (2 hours)

Goals:

• To generalize and systematize knowledge on solving trigonometric equations of various types.
• To promote the development of students' mathematical thinking, the ability to observe, compare, generalize, classify.
• Encourage students to overcome difficulties in the process of mental activity, to self-control, introspection of their activities.

Equipment for the lesson: KRMu, laptops for each student.

Lesson structure:

1. Organizational moment
2. Discussion d / h and samot. works of the last lesson
3. Repetition of methods for solving trigonometric equations.
4. Solving trigonometric equations
5. Selection of roots in trigonometric equations.
6. Independent work.
7. Lesson summary. Homework.

1. Organizational moment (2 min.)

The teacher greets the audience, announces the topic of the lesson and the work plan.

2. a) Review of homework (5 min.)

The goal is to check execution. One work with the help of a video camera is displayed on the screen, the rest are selectively collected for the teacher's check.

b) Analysis of independent work (3 min.)

The goal is to analyze the mistakes, indicate the ways to overcome them.

On the screen, answers and solutions, students have their work pre-assigned. Analysis is progressing quickly.

3. Repetition of methods for solving trigonometric equations (5 min.)

The goal is to recall the methods for solving trigonometric equations.

Ask students what methods they know for solving trigonometric equations. Emphasize that there are so-called basic (frequently used) methods:

• variable replacement,
• factorization,
• homogeneous equations,

and there are applied methods:

• according to the formulas for converting a sum into a product and a product into a sum,
• by the degree reduction formulas,
• universal trigonometric substitution
• introduction of an auxiliary angle,
• multiplication by some trigonometric function.

It should also be remembered that one equation can be solved in different ways.

4. Solving trigonometric equations (30 min.)

The goal is to generalize and consolidate knowledge and skills on this topic, to prepare for the decision of C1 from the exam.

I consider it expedient to solve the equations for each method together with the students.

The student dictates the decision, the teacher writes it down on the tablet, the whole process is displayed on the screen. This will allow you to quickly and efficiently recall the previously covered material.

Solve equations:

1) change of variable 6cos 2 x + 5sinx - 7 = 0

2) factoring 3cos (x / 3) + 4cos 2 (x / 3) = 0

3) homogeneous equations sin 2 x + 3cos 2 x - 2sin2x = 0

4) converting the sum to the product cos5x + cos7x = cos (π + 6x)

5) converting the product to the sum 2sinx sin2x + cos3x = 0

6) lowering the power sin2x - sin 2 2x + sin 2 3x = 0.5

7) universal trigonometric substitution sinx + 5cosx + 5 = 0.

Solving this equation, it should be noted that the use of this method leads to a narrowing of the domain of definition, since the sine and cosine are replaced by tg (x / 2). Therefore, before writing out the answer, you need to check whether the numbers from the set π + 2πn, n Z are horses of this equation.

8) introduction of an auxiliary angle √3sinx + cosx - √2 = 0

9) multiplication by some trigonometric function cosx cos2x cos4x = 1/8.

5. Selection of roots of trigonometric equations (20 min.)

Since in conditions of fierce competition when entering universities, solving one first part of the exam is not enough, most students should pay attention to the tasks of the second part (C1, C2, C3).

Therefore, the purpose of this stage of the lesson is to recall the previously studied material, to prepare for solving the C1 problem from the Unified State Examination in 2011.

There are trigonometric equations in which you need to select roots when writing out an answer. This is due to some restrictions, for example: the denominator of the fraction is not zero, the expression under the even root is non-negative, the expression under the sign of the logarithm is positive, etc.

Such equations are considered equations of increased complexity and in the version of the exam are in the second part, namely C1.

Solve the equation:

The fraction is zero if then using the unit circle, we select the roots (see Figure 1)

Picture 1.

we get x = π + 2πn, n Z

Answer: π + 2πn, n Z

On the screen, the selection of roots is shown on a circle in a color image.

The product is equal to zero when at least one of the factors is equal to zero, and the arc, in this case, does not lose its meaning. Then

Select the roots using the unit circle (see Figure 2)

Figure 2.

5)

Let's go to the system:

In the first equation of the system, we make the change log 2 (sinx) = y, we get the equation then , back to the system

select the roots using the unit circle (see Figure 5),

Figure 5.

6. Independent work (15 min.)

The goal is to consolidate and check the assimilation of the material, to identify errors, to outline ways to correct them.

The work is offered in three versions, prepared in advance on a printed basis, for the choice of students.

You can solve equations in any way.

Option for "3"

Solve equations:

1) 2sin 2 x + sinx - 1 = 0

2) sin2x = √3cosx

Option for "4"

Solve equations:

1) cos2x = 11sinx - 5

2) (2sinx + √3) log 8 (cosx) = 0

Option for "5"

Solve equations:

1) 2sinx - 3cosx = 2

2)

7. Lesson summary, homework (5 min.)

The teacher summarizes the lesson, once again draws attention to the fact that the trigonometric equation can be solved in several ways. The best way to achieve quick results is the one that is best learned by the individual student.

When preparing for the exam, you need to systematically repeat formulas and methods for solving equations.

Homework (prepared in advance on a printed basis) is distributed and comments are made on how to solve some equations.

Solve equations:

1) cosx + cos5x = cos3x + cos7x

2) 5sin (x / 6) - cos (x / 3) + 3 = 0

3) 4sin 2 x + sin2x = 3

4) sin 2 x + sin 2 2x - sin 2 3x - sin 2 4x = 0

5) cos3x cos6x = cos4x cos7x

6) 4sinx - 6cosx = 1

7) 3sin2x + 4 cos2x = 5

8) cosx cos2x cos4x cos8x = (1/8) cos15x

9) (2sin 2 x - sinx) log 3 (2cos 2 x + cosx) = 0

10) (2cos 2 x - √3cosx) log 7 (-tgx) = 0

11)

Voronkova Olga Ivanovna

MBOU "Secondary school

No. 18 "

Engels, Saratov region.

Mathematic teacher.

"Trigonometric expressions and their transformations"

Introduction ……………………………………………………………………… .... 3

Chapter 1 Classification of tasks for the use of transformations of trigonometric expressions …………………………. …………………… ... 5

1.1. Calculation tasks values ​​of trigonometric expressions ……… .5

1.2.Trigonometric Expression Simplification Tasks ... 7

1.3. Tasks for converting numeric trigonometric expressions ... ..7

1.4 Mixed type assignments ………………………………………………… ..... 9

Chapter 2. Methodological aspects of the organization of the final repetition of the topic "Transformation of trigonometric expressions" …………………………… 11

2.1 Thematic repetition in grade 10 ……………………………………… ... 11

Test 1 …………………………………………………………………………… ..12

Test 2 …………………………………………………………………………… ..13

Test 3 …………………………………………………………………………… ..14

2.2 Final repetition in grade 11 ………………………………………… ... 15

Test 1 …………………………………………………………………………… ..17

Test 2 …………………………………………………………………………… ..17

Test 3 …………………………………………………………………………… ..18

Conclusion. ………………………………………………………………… ....... 19

List of used literature ……………………………………… .. …… .20

Introduction.

In today's conditions, the most important question is: "How can we help eliminate some gaps in the knowledge of students and warn them against possible mistakes on the exam?" To solve this issue, it is necessary to seek from students not formal assimilation of the program material, but its deep and conscious understanding, the development of the speed of oral calculations and transformations, as well as the development of skills for solving simple problems "in the mind." It is necessary to convince students that only if there is an active position, in the study of mathematics, provided that they acquire practical skills, skills and their use, one can count on real success. It is necessary to use every opportunity to prepare for the exam, including elective subjects in grades 10-11, regularly analyze difficult tasks with students, choosing the most rational way of solving in the lessons and additional classes.Positive result inareas for solving typical problems can be achieved if mathematics teachers, creatinggood basic training of students, look for new ways in solving the problems that have opened before us, actively experiment, apply modern pedagogical technologies, methods, techniques that create favorable conditions for effective self-realization and self-determination of students in new social conditions.

Trigonometry is an integral part of the school mathematics course. Good knowledge and solid skills in trigonometry are evidence of a sufficient level of mathematical culture, an indispensable condition for the successful study of mathematics, physics, a number of technical disciplines.

Relevance of work. A significant part of school graduates shows from year to year very poor preparation in this important section of mathematics, as evidenced by the results of previous years (the percentage of completion in 2011 - 48.41%, 2012 - 51.05%), since the analysis of passing the unified state exam showed that students make many mistakes when completing the assignments of this particular section or do not take on such assignments at all. In One In the state exam, trigonometry questions are found in almost three types of assignments. This is the solution of the simplest trigonometric equations in task B5, and work with trigonometric expressions in task B7, and the study of trigonometric functions in task B14, as well as task B12, which have formulas that describe physical phenomena and contain trigonometric functions. And this is only part of B's ​​tasks! But there are also favorite trigonometric equations with the selection of C1 roots, and "not very favorite" geometric tasks C2 and C4.

Objective. Analyze the material of the Unified State Exam of tasks B7, devoted to transformations of trigonometric expressions and classify the tasks according to the form of their presentation in the tests.

The work consists of two chapters, an introduction and a conclusion. The introduction emphasizes the relevance of the work. The first chapter provides a classification of tasks for the use of transformations of trigonometric expressions in test tasks of the Unified State Exam (2012).

In the second chapter, the organization of the repetition of the topic "Transformation of trigonometric expressions" in grades 10, 11 is considered, and tests on this topic are developed.

The literature list includes 17 sources.

Chapter 1. Classification of tasks for using transformations of trigonometric expressions.

In accordance with the standard of secondary (complete) education and the requirements for the level of training of students, tasks for knowledge of the basics of trigonometry are included in the requirements codifier.

Learning the basics of trigonometry will be most effective when:

positive motivation of students to repeat previously studied material will be provided;

a student-centered approach will be implemented in the educational process;

a system of tasks will be applied that contributes to the expansion, deepening, systematization of students' knowledge;

advanced pedagogical technologies will be used.

Having analyzed the literature and Internet resources on preparing for the exam, we proposed one of the possible classifications of tasks B7 (KIM USE 2012-trigonometry): tasks for calculatingvalues ​​of trigonometric expressions; assignments forconverting numeric trigonometric expressions; tasks for converting alphabetic trigonometric expressions; mixed tasks.

1.1. Calculation tasks values ​​of trigonometric expressions.

One of the most common types of simple trigonometry problems is calculating the values ​​of trigonometric functions by the value of one of them:

a) Using the basic trigonometric identity and its consequences.

Example 1 ... Find if
and
.

Solution.
,
,

Because , then
.

Answer.

Example 2 ... Find
, if
and .

Solution.
,
,
.

Because , then
.

Answer. ...

b) Using double angle formulas.

Example 3 ... Find
, if
.

Solution. , .

Answer.
.

Example 4 ... Find the meaning of the expression
.

Solution. ...

Answer.
.

1. Find , if
and
... Answer. -0.2

2. Find , if
and
... Answer. 0,4

3. Find
, if . Answer. -12.884. Find
, if
... Answer. -0.845. Find the meaning of the expression:
... Answer. 66. Find the meaning of the expression
.Answer. -nineteen

1.2.Tasks to simplify trigonometric expressions. Coercion formulas should be well mastered by students, as they will find further application in the lessons of geometry, physics and other related disciplines.

Example 5 . Simplify expressions
.

Solution. ...

Answer.
.

Tasks for independent solution:

1. Simplify the expression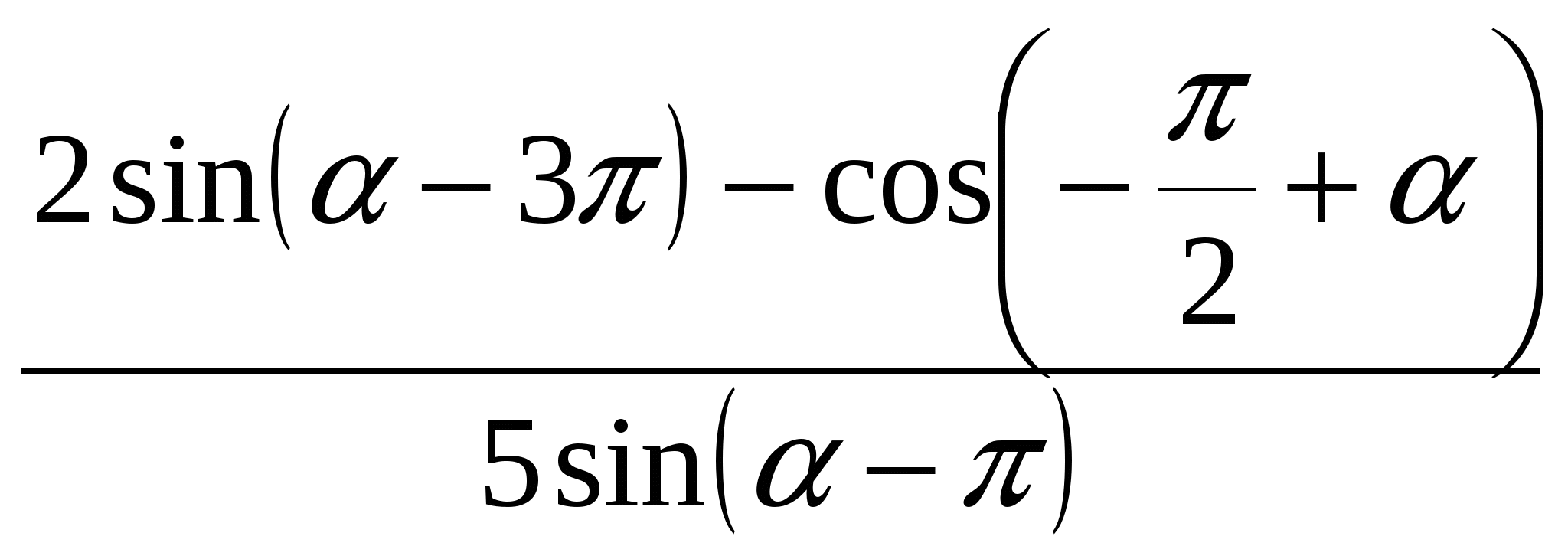
. Answer. 0.62. Find
, if
and... Answer. 10.563. Find the meaning of the expression
, if
. Answer. 2

1.3. Tasks for converting numeric trigonometric expressions.

When practicing the skills and abilities of tasks for the transformation of numerical trigonometric expressions, you should pay attention to the knowledge of the table of values ​​of trigonometric functions, the properties of parity and periodicity of trigonometric functions.

a) Using the exact values ​​of trigonometric functions for some angles.

Example 6 ... Calculate
.

Solution.
.

Answer.
.

b) Using parity properties trigonometric functions.

Example 7 ... Calculate
.

Solution. .

Answer.

v) Using periodicity propertiestrigonometric functions.

Example 8 . Find the meaning of the expression
.

Solution. ...

Answer.
.

Tasks for independent solution:

1. Find the meaning of the expression
. Answer. -40.52. Find the meaning of the expression
. Answer. 17

3. Find the meaning of the expression
. Answer. 6

. Answer. -24
Answer. -64

1.4 Mixed assignments.

The test form of certification has very significant features, so it is important to pay attention to the tasks associated with the use of several trigonometric formulas at the same time.

Example 9. Find
, if
.

Solution.
.

Answer.
.

Example 10 ... Find
, if
and
.

Solution. .

Because , then
.

Answer.
.

Example 11. Find
, if .

Solution. , ,
,
,
,
,
.

Answer.

Example 12. Calculate
.

Solution. .

Answer.
.

Example 13. Find the meaning of the expression
, if
.

Solution. .

Answer.
.

Tasks for independent solution:

1. Find
, if
. Answer. -1.75
2. Find
, if
. Answer. 33. Find
, if .Answer. 0.254. Find the meaning of the expression
, if
. Answer. 0.35. Find the meaning of the expression
, if
. Answer. 5

Chapter 2. Methodological aspects of the organization of the final repetition of the topic "Transformation of trigonometric expressions."

One of the most important issues contributing to the further increase in academic performance, the achievement of deep and lasting knowledge among students is the question of repetition of previously passed material. Practice shows that in grade 10 it is more expedient to organize a thematic repetition; in grade 11 - final repetition.

2.1. Thematic repetition in grade 10.

In the process of working on mathematical material, it is especially important to repeat each completed topic or an entire section of the course.

With a thematic repetition, students' knowledge on a topic is systematized at the final stage of its passage or after a break.

For thematic repetition, special lessons are allocated, on which the material of one topic is concentrated and generalized.

Repetition in the lesson is carried out through a conversation with the wide involvement of students in this conversation. After that, students are asked to repeat a specific topic and are warned that test work will be carried out.

A test on a topic should include all of its core questions. After completing the work, the analysis of typical errors is carried out and repetition is organized to eliminate them.

For the lessons of thematic repetition, we offer the developed test papers on the topic "Conversion of trigonometric expressions."

Test No. 1

Test number 2

Test number 3

Answer table

Test

2.2. Final repetition in grade 11.

The final repetition is carried out at the final stage of the study of the main issues of the mathematics course and is carried out in a logical connection with the study of the educational material for this section or the course as a whole.

The final repetition of the training material has the following goals:

1. Activation of the material of the entire training course to clarify its logical structure and build a system within subject and inter-subject connections.

2. Deepening and, if possible, expanding the knowledge of students on the main issues of the course in the process of repetition.

Given the compulsory mathematics exam for all graduates, the gradual introduction of the USE forces teachers to take a new approach to preparing and delivering lessons, taking into account the need to ensure that all schoolchildren master the educational material at a basic level, as well as the opportunity for motivated students interested in obtaining high scores for admission to a university, dynamic progress in mastering the material at an advanced and high level.

In the lessons of the final repetition, you can consider the following tasks:

Example 1 . Calculate the value of the expression.Solution. =
= =
=
=
=
=0,5. Answer. 0.5. Example 2. Specify the largest integer value that the expression can take
.

Solution. Because
can take any value belonging to the segment [–1; 1], then
takes any value of the segment [–0.4; 0.4], therefore. The integer value of the expression is one - the number 4.

Answer: 4 Example 3 . Simplify the expression
.

Solution: Let's use the formula for factoring the sum of cubes:. We have

We have:
.

Answer: 1

Example 4. Calculate
.

Solution. ...

Answer: 0.28

For the lessons of the final repetition, we offer developed tests on the topic "Transformation of trigonometric expressions".

Please enter the largest integer not exceeding 1

Conclusion.

Having worked through the relevant methodological literature on this topic, we can conclude that the ability and skills to solve tasks related to trigonometric transformations in the school mathematics course is very important.

In the course of the work done, the classification of tasks B7 was carried out. Trigonometric formulas most often used in CMMs of 2012 are considered. Examples of tasks with solutions are given. Differentiable tests have been developed to organize repetition and systematization of knowledge in preparation for the exam.

It is advisable to continue the work begun by considering solution of the simplest trigonometric equations in task B5, study of trigonometric functions in task B14, task B12, which contain formulas describing physical phenomena and containing trigonometric functions.

In conclusion, I would like to note that the effectiveness of passing the USE is largely determined by how effectively the preparation process is organized at all levels of education, with all categories of students. And if we manage to form students' independence, responsibility and readiness to continue learning throughout their subsequent life, then we will not only fulfill the order of the state and society, but also raise our own self-esteem.

Repetition of the teaching material requires creative work from the teacher. He must provide a clear connection between the types of repetition, implement a deeply thought-out repetition system. Mastering the art of organizing repetition is the teacher's task. The strength of students' knowledge largely depends on its solution.

Literature.

Vygodsky Ya.Ya., Handbook of elementary mathematics. -M .: Nauka, 1970.

Problems of increased difficulty in algebra and the principles of analysis: Textbook for 10-11 grades of secondary school / B.M. Ivlev, A.M. Abramov, Yu.P. Dudnitsyn, S.I. Schwarzburd. - M .: Education, 1990.

Application of basic trigonometric formulas to the transformation of expressions (10th grade) // Festival of pedagogical ideas. 2012-2013.

A.G. Koryanov , Prokofiev A.A. We prepare good students and excellent students for the exam. - M .: Pedagogical University "September First", 2012. - 103 p.

Kuznetsova E.N. Simplification of trigonometric expressions. Solving trigonometric equations by various methods (preparation for the exam). 11th grade. 2012-2013.

Kulanin E. D. 3000 Competition Problems in Mathematics. 4th them., Rev. and add. - M .: Rolf, 2000.

Mordkovich A.G. Methodical problems of studying trigonometry in secondary school // Mathematics in school. 2002. No. 6.

Pichurin L.F. About trigonometry and not only about it: -M. Education, 1985

Reshetnikov N.N. Trigonometry at school: -M. : Pedagogical University "September First", 2006, lk 1.

Shabunin M.I., Prokofiev A.A. Mathematics. Algebra. Beginning of mathematical analysis. Profile level: textbook for grade 10 - M .: BINOM. Knowledge laboratory, 2007.

Educational portal for preparing for the exam.

Preparing for the exam in mathematics "Oh, this trigonometry! http://festival.1september.ru/articles/621971/

Project "Mathematics? Easy !!!" http://www.resolventa.ru/

The video lesson "Simplifying Trigonometric Expressions" is designed to develop students' skills in solving trigonometric problems using basic trigonometric identities. In the course of the video lesson, the types of trigonometric identities are considered, examples of solving problems using them. By using the visual aid, it is easier for the teacher to achieve the lesson objectives. A vivid presentation of the material helps to remember important points. The use of animation effects and dubbing make it possible to completely replace the teacher at the stage of explaining the material. Thus, using this visual aid in mathematics lessons, the teacher can increase the effectiveness of teaching.

At the beginning of the video lesson, its topic is announced. Then the trigonometric identities studied earlier are recalled. The screen displays the equalities sin 2 t + cos 2 t = 1, tg t = sin t / cos t, where t ≠ π / 2 + πk for kϵZ, ctg t = cos t / sin t, valid for t ≠ πk, where kϵZ, tg t · ctg t = 1, for t ≠ πk / 2, where kϵZ, called the basic trigonometric identities. It is noted that these identities are often used in solving problems where it is necessary to prove equality or simplify an expression.

Further, examples of the application of these identities in solving problems are considered. First, it is proposed to consider the solution of problems to simplify expressions. In example 1, it is necessary to simplify the expression cos 2 t- cos 4 t + sin 4 t. To solve the example, first place the common factor cos 2 t outside the brackets. As a result of such a transformation in parentheses, the expression 1- cos 2 t is obtained, the value of which from the basic identity of trigonometry is equal to sin 2 t. After transforming the expression, it is obvious that one more common factor sin 2 t can be parenthesized, after which the expression takes the form sin 2 t (sin 2 t + cos 2 t). From the same basic identity, we derive the value of the expression in parentheses, equal to 1. As a result of simplification, we obtain cos 2 t- cos 4 t + sin 4 t = sin 2 t.

Example 2 also needs to simplify the expression cost / (1- sint) + cost / (1+ sint). Since the expression cost is in the numerators of both fractions, it can be bracketed as a common factor. Then the fractions in parentheses are reduced to a common denominator by multiplying (1-sint) (1+ sint). After bringing similar terms in the numerator remains 2, and in the denominator 1 - sin 2 t. On the right side of the screen, the basic trigonometric identity sin 2 t + cos 2 t = 1 is reminded. Using it, we find the denominator of the fraction cos 2 t. After reducing the fraction, we get a simplified form of the expression cost / (1- sint) + cost / (1+ sint) = 2 / cost.

Further, examples of proof of identities are considered, in which the knowledge gained about the basic identities of trigonometry is applied. In example 3, it is necessary to prove the identity (tg 2 t-sin 2 t) · ctg 2 t = sin 2 t. On the right side of the screen, three identities are displayed that will be needed for the proof - tg t · ctg t = 1, ctg t = cos t / sin t and tan t = sin t / cos t with restrictions. To prove the identity, first the parentheses are expanded, after which a product is formed that reflects the expression of the main trigonometric identity tg t · ctg t = 1. Then, according to the identity from the definition of the cotangent, ctg 2 t is transformed. As a result of the transformations, the expression 1-cos 2 t is obtained. Using the basic identity, we find the meaning of the expression. Thus, it has been proved that (tan 2 t-sin 2 t) ctg 2 t = sin 2 t.

In example 4, you need to find the value of the expression tg 2 t + ctg 2 t if tg t + ctg t = 6. To calculate the expression, first the right and left sides of the equality (tg t + ctg t) 2 = 6 2 are squared. The abbreviated multiplication formula resembles on the right side of the screen. After expanding the parentheses on the left side of the expression, the sum tg 2 t + 2 · tg t · ctg t + ctg 2 t is formed, for the transformation of which one of the trigonometric identities tg t · ctg t = 1 can be applied, the form of which is reminded on the right side of the screen. After the transformation, the equality tg 2 t + ctg 2 t = 34 is obtained. The left side of the equality coincides with the condition of the problem, so the answer is 34. The problem is solved.

The video lesson "Simplifying Trigonometric Expressions" is recommended for use in a traditional school mathematics lesson. Also, the material will be useful for a teacher carrying out distance learning. In order to develop skills in solving trigonometric problems.

TEXT CODE:

"Simplification of trigonometric expressions."

Equality

1) sin 2 t + cos 2 t = 1 (sine square te plus cosine square te equals one)

2) tgt =, for t ≠ + πk, kϵZ (the tangent te is equal to the ratio of the sine te to the cosine te when te is not equal to pi by two plus pi ka, ka belongs to zet)

3) ctgt =, for t ≠ πk, kϵZ (the cotangent te is equal to the ratio of the cosine te to the sine te when te is not equal to the peak, ka belongs to z).

4) tgt ∙ ctgt = 1 for t ≠, kϵZ (the product of the tangent te and the cotangent te is equal to one if te is not equal to the peak, divided by two, ka belongs to z)

are called basic trigonometric identities.

They are often used to simplify and prove trigonometric expressions.

Let's look at examples of using these formulas to simplify trigonometric expressions.

EXAMPLE 1: Simplify the expression: cos 2 t - cos 4 t + sin 4 t. (the expression is a cosine squared te minus the fourth degree cosine te plus the fourth degree sine te).

Solution. cos 2 t - cos 4 t + sin 4 t = cos 2 t ∙ (1 - cos 2 t) + sin 4 t = cos 2 t ∙ sin 2 t + sin 4 t = sin 2 t (cos 2 t + sin 2 t) = sin 2 t 1 = sin 2 t

(we take out the common factor cosine squared te, in brackets we get the difference between unity and the square of the cosine te, which is equal by the first identity to the square of the sine te. We get the sum of the sine of the fourth degree te of the product cosine square te and sine square te. in parentheses, in parentheses we get the sum of the squares of the cosine and sine, which by the basic trigonometric identity is equal to 1. As a result, we get the square of the sine te).

EXAMPLE 2: Simplify the expression: +.

(expression ba is the sum of two fractions in the numerator of the first cosine te in the denominator one minus sine te, in the numerator of the second cosine te in the denominator the second unit plus sine te).

(Let's take the common factor cosine te out of the brackets, and in parentheses we bring it to the common denominator, which is the product of one minus sine te and one plus sine te.

In the numerator we get: one plus sine te plus one minus sine te, we give similar ones, the numerator is equal to two after bringing similar ones.

In the denominator, you can apply the formula of abbreviated multiplication (difference of squares) and get the difference between the unit and the square of the sine te, which, according to the basic trigonometric identity

is equal to the square of the cosine te. After canceling by cosine te we get the final answer: two divided by cosine te).

Let's consider examples of using these formulas in proving trigonometric expressions.

EXAMPLE 3. Prove the identity (tg 2 t - sin 2 t) ∙ ctg 2 t = sin 2 t (the product of the difference between the squares of the tangent te and sine te and the square of the cotangent te is equal to the square of the sine te).

Proof.

Let's transform the left side of the equality:

(tg 2 t - sin 2 t) ∙ ctg 2 t = tg 2 t ∙ ctg 2 t - sin 2 t ∙ ctg 2 t = 1 - sin 2 t ∙ ctg 2 t = 1 - sin 2 t ∙ = 1 - cos 2 t = sin 2 t

(Let's open the brackets, from the previously obtained relation it is known that the product of the squares of the tangent te and the cotangent te is equal to one. Recall that the cotangent te is equal to the ratio of the cosine te to the sine te, which means that the square of the cotangent is the ratio of the square of the cosine te and the square of the sine te.

After canceling the square te by sine, we get the difference between the unit and the cosine of the square te, which is equal to the sine of the square te). Q.E.D.

EXAMPLE 4 Find the value of the expression tg 2 t + ctg 2 t if tgt + ctgt = 6.

(the sum of the squares of the tangent te and the cotangent te, if the sum of the tangent and cotangent is six).

Solution. (tgt + ctgt) 2 = 6 2

tg 2 t + 2 ∙ tgt ∙ ctgt + ctg 2 t = 36

tg 2 t + 2 + ctg 2 t = 36

tg 2 t + ctg 2 t = 36-2

tg 2 t + ctg 2 t = 34

Let's square both sides of the original equality:

(tgt + ctgt) 2 = 6 2 (the square of the sum of the tangent te and the cotangent te is six squared). Recall the formula for abbreviated multiplication: The square of the sum of two quantities is equal to the square of the first plus twice the product of the first by the second plus the square of the second. (a + b) 2 = a 2 + 2ab + b 2 We get tg 2 t + 2 ∙ tgt ∙ ctgt + ctg 2 t = 36 (tangent square te plus double product of tangent te and cotangent te plus cotangent squared te equals thirty-six) ...

Since the product of the tangent te and the cotangent te is equal to one, then tg 2 t + 2 + ctg 2 t = 36 (the sum of the squares of the tangent te and the cotangent te and two is thirty-six),