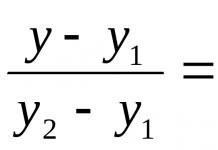The coordinate method is a very effective and versatile way of finding any angles or distances between stereometric objects in space. If your math tutor is highly qualified, then he should know this. Otherwise, I would advise you to change the tutor for the "C" part. My preparation for the exam in mathematics C1-C6 usually includes an analysis of the basic algorithms and formulas described below.
Angle between straight lines a and b
The angle between straight lines in space is the angle between any intersecting straight lines parallel to them. This angle is equal to the angle between the direction vectors of these straight lines (or complements it up to 180 degrees).
What algorithm does a math tutor use to find an angle?
1) Choose any vectors 
and, having the directions of straight lines a and b (parallel to them).
2) Determine the coordinates of the vectors and by the corresponding coordinates of their beginnings and ends (the coordinates of the beginning must be subtracted from the coordinates of the end of the vector).
3) Substitute the found coordinates into the formula:
... To find the angle itself, you need to find the inverse cosine of the result.
Normal to plane
Any vector perpendicular to this plane is called normal to a plane.
How to find the normal? To find the coordinates of the normal, it is enough to find out the coordinates of any three points M, N and K lying in a given plane. Using these coordinates, we find the coordinates of the vectors and and require the fulfillment of the conditions and. Equating the scalar product of vectors to zero, we compose a system of equations with three variables, from which the coordinates of the normal can be found.
Math Tutor's Note : It is not at all necessary to solve the system completely, because it is enough to choose at least one normal. To do this, you can substitute any number (for example, one) instead of any of its unknown coordinates and solve the system of two equations with the remaining two unknowns. If it has no solutions, then this means that in the family of normals there is no one that has one for the selected variable. Then substitute one for another variable (another coordinate) and solve a new system. If you miss again, then your normal will have one in the last coordinate, and it itself will turn out to be parallel to some coordinate plane (in this case, it is easy to find it without a system).
Suppose that we are given a straight line and a plane by the coordinates of the direction vector and the normal
The angle between a straight line and a plane is calculated using the following formula:
Let and be any two normals to the given planes. 
Then the cosine of the angle between the planes is equal to the modulus of the cosine of the angle between the normals:
Equation of a plane in space
The points satisfying the equality form a plane with the normal. The coefficient is responsible for the amount of deviation (parallel shift) between two planes with the same specified normal. In order to write the equation of the plane, you first need to find its normal (as described above), and then substitute the coordinates of any point on the plane along with the coordinates of the found normal into the equation and find the coefficient.
In order to use the coordinate method, you need to know the formulas well. There are three of them:
At first glance, it looks menacing, but just a little practice and everything will work great.
Task. Find the cosine of the angle between vectors a = (4; 3; 0) and b = (0; 12; 5).
Solution. Since the coordinates of the vectors are given to us, we substitute them in the first formula:
Task. Make an equation for the plane passing through the points M = (2; 0; 1), N = (0; 1; 1) and K = (2; 1; 0), if it is known that it does not pass through the origin.
Solution. The general equation of the plane: Ax + By + Cz + D = 0, but since the desired plane does not pass through the origin of coordinates - the point (0; 0; 0) - then we put D = 1. Since this plane passes through the points M, N and K, then the coordinates of these points should turn the equation into the correct numerical equality.
Substitute instead of x, y and z coordinates of the point M = (2; 0; 1). We have:
A 2 + B 0 + C 1 + 1 = 0 ⇒ 2A + C + 1 = 0;
Similarly, for the points N = (0; 1; 1) and K = (2; 1; 0) we obtain the equations:
A 0 + B 1 + C 1 + 1 = 0 ⇒ B + C + 1 = 0;
A 2 + B 1 + C 0 + 1 = 0 ⇒ 2A + B + 1 = 0;
So, we have three equations and three unknowns. Let's compose and solve the system of equations:
We got that the equation of the plane has the form: - 0.25x - 0.5y - 0.5z + 1 = 0.
Task. The plane is given by the equation 7x - 2y + 4z + 1 = 0. Find the coordinates of the vector perpendicular to the given plane.
Solution. Using the third formula, we get n = (7; - 2; 4) - that's all!
Calculating the coordinates of vectors
But what if there are no vectors in the problem - there are only points lying on straight lines, and you need to calculate the angle between these straight lines? It's simple: knowing the coordinates of the points - the beginning and end of the vector - you can calculate the coordinates of the vector itself.
To find the coordinates of a vector, subtract the coordinates of the beginning from the coordinates of its end.
This theorem works in the same way both on the plane and in space. The expression "subtract coordinates" means that the x coordinate of another is subtracted from the x coordinate of one point, then the same must be done with the y and z coordinates. Here are some examples:
Task. There are three points in space, given by their coordinates: A = (1; 6; 3), B = (3; - 1; 7) and C = (- 4; 3; - 2). Find the coordinates of vectors AB, AC and BC.
Consider a vector AB: its origin is at point A, and its end is at point B. Therefore, to find its coordinates, it is necessary to subtract the coordinates of point A from the coordinates of point B:
AB = (3 - 1; - 1 - 6; 7 - 3) = (2; - 7; 4).
Similarly, the beginning of the vector AC is still the same point A, but the end is point C. Therefore, we have:
AC = (- 4 - 1; 3 - 6; - 2 - 3) = (- 5; - 3; - 5).
Finally, to find the coordinates of the vector BC, you need to subtract the coordinates of point B from the coordinates of point C:
BC = (- 4 - 3; 3 - (- 1); - 2 - 7) = (- 7; 4; - 9).
Answer: AB = (2; - 7; 4); AC = (- 5; - 3; - 5); BC = (- 7; 4; - 9)
Pay attention to the calculation of the coordinates of the last BC vector: many people make mistakes when working with negative numbers... This concerns the variable y: point B has y = - 1, and point C y = 3. We get exactly 3 - (- 1) = 4, and not 3 - 1, as many believe. Don't make such stupid mistakes!
Calculation of direction vectors for straight lines
If you read Problem C2 carefully, you will be surprised to find that there are no vectors there. There are only straight lines and planes.
Let's start with the straight lines. Everything is simple here: on any straight line there are at least two different points and, conversely, any two different points define a single straight line ...
Does anyone understand what is written in the previous paragraph? I didn’t understand it myself, so I’ll explain it easier: in problem C2, straight lines are always given by a pair of points. If we introduce a coordinate system and consider a vector with a beginning and an end at these points, we get the so-called direction vector for a straight line:
Why is this vector needed? The point is that the angle between two straight lines is the angle between their direction vectors. Thus, we pass from incomprehensible straight lines to specific vectors, the coordinates of which are easy to calculate. How easy is it? Take a look at examples:
Task. In the cube ABCDA 1 B 1 C 1 D 1 lines AC and BD 1 are drawn. Find the coordinates of the direction vectors of these lines.
Since the length of the edges of the cube is not specified in the condition, we set AB = 1. We introduce a coordinate system with the origin at point A and axes x, y, z directed along lines AB, AD and AA 1, respectively. The unit segment is equal to AB = 1.
Now we will find the coordinates of the direction vector for the line AC. We need two points: A = (0; 0; 0) and C = (1; 1; 0). From here we obtain the coordinates of the vector AC = (1 - 0; 1 - 0; 0 - 0) = (1; 1; 0) - this is the direction vector.
Now let's deal with the straight line BD 1. It also has two points: B = (1; 0; 0) and D 1 = (0; 1; 1). We get the direction vector BD 1 = (0 - 1; 1 - 0; 1 - 0) = (- 1; 1; 1).
Answer: AC = (1; 1; 0); BD 1 = (- 1; 1; 1)
Task. In a regular triangular prism ABCA 1 B 1 C 1, all edges of which are equal to 1, lines AB 1 and AC 1 are drawn. Find the coordinates of the direction vectors of these lines.
Let's introduce the coordinate system: the origin is at point A, the x-axis coincides with AB, the z-axis coincides with AA 1, the y-axis forms the OXY plane with the x-axis, which coincides with the ABC plane.
First, let's deal with the straight line AB 1. Everything is simple here: we have points A = (0; 0; 0) and B 1 = (1; 0; 1). We get the direction vector AB 1 = (1 - 0; 0 - 0; 1 - 0) = (1; 0; 1).
Now we will find the direction vector for AC 1. All the same - the only difference is that point C 1 has irrational coordinates. So, A = (0; 0; 0), so we have:
Answer: AB 1 = (1; 0; 1);
A small but very important note about the last example. If the origin of the vector coincides with the origin, the calculations are greatly simplified: the coordinates of the vector are simply equal to the coordinates of the end. Unfortunately, this is only true for vectors. For example, when working with planes, the presence of the origin on them only complicates the calculations.
Calculating normal vectors for planes
Normal vectors are not vectors that do or do well. By definition, a normal vector (normal) to a plane is a vector perpendicular to that plane.
In other words, a normal is a vector perpendicular to any vector in a given plane. Surely you have met such a definition - however, instead of vectors, we were talking about straight lines. However, just above it was shown that in problem C2 you can operate with any convenient object - even a straight line, even a vector.
Let me remind you once again that any plane is defined in space by the equation Ax + By + Cz + D = 0, where A, B, C, and D are some coefficients. Without loss of generality of the solution, we can assume D = 1 if the plane does not pass through the origin, or D = 0 if it does. In any case, the coordinates of the normal vector to this plane are n = (A; B; C).
So, the plane can also be successfully replaced by a vector - the same normal. Any plane is defined in space by three points. How to find the equation of the plane (and therefore the normal), we have already discussed at the very beginning of the article. However, this process causes problems for many, so I will give a couple more examples:
Task. Section A 1 BC 1 is drawn in the cube ABCDA 1 B 1 C 1 D 1. Find the normal vector for the plane of this section if the origin is at point A, and the x, y, and z axes coincide with the edges AB, AD and AA 1, respectively.
Since the plane does not go through the origin, its equation looks like this: Ax + By + Cz + 1 = 0, i.e. coefficient D = 1. Since this plane passes through points A 1, B and C 1, the coordinates of these points turn the equation of the plane into the correct numerical equality.
A 0 + B 0 + C 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = - 1;
Similarly, for points B = (1; 0; 0) and C 1 = (1; 1; 1) we obtain the equations:
A 1 + B 0 + C 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = - 1;
A 1 + B 1 + C 1 + 1 = 0 ⇒ A + B + C + 1 = 0;
But we already know the coefficients A = - 1 and C = - 1, so it remains to find the coefficient B:
B = - 1 - A - C = - 1 + 1 + 1 = 1.
We get the equation of the plane: - A + B - C + 1 = 0, Therefore, the coordinates of the normal vector are equal to n = (- 1; 1; - 1).
Task. Section AA 1 C 1 C is drawn in the cube ABCDA 1 B 1 C 1 D 1. Find the normal vector for the plane of this section if the origin is at point A, and the x, y, and z axes coincide with the edges AB, AD and AA 1 respectively.
In this case, the plane passes through the origin, so the coefficient D = 0, and the plane equation looks like this: Ax + By + Cz = 0. Since the plane passes through the points A1 and C, the coordinates of these points turn the plane equation into the correct numerical equality.
Substitute instead of x, y and z coordinates of the point A 1 = (0; 0; 1). We have:
A 0 + B 0 + C 1 = 0 ⇒ C = 0;
Similarly, for the point C = (1; 1; 0) we get the equation:
A 1 + B 1 + C 0 = 0 ⇒ A + B = 0 ⇒ A = - B;
We put B = 1. Then A = - B = - 1, and the equation of the whole plane has the form: - A + B = 0, Therefore, the coordinates of the normal vector are equal to n = (- 1; 1; 0).
Generally speaking, in the above problems it is necessary to compose a system of equations and solve it. There will be three equations and three variables, but in the second case one of them will be free, i.e. take arbitrary values. That is why we have the right to put B = 1 - without prejudice to the generality of the solution and the correctness of the answer.
Very often in the C2 problem it is required to work with points that divide the segment in half. The coordinates of such points are easily calculated if the coordinates of the ends of the segment are known.
So, let the segment be defined by its ends - the points A = (x a; y a; z a) and B = (x b; y b; z b). Then the coordinates of the midpoint of the segment - we denote it by the point H - can be found by the formula:
In other words, the coordinates of the midpoint of a segment are the arithmetic mean of the coordinates of its ends.
Task. The unit cube ABCDA 1 B 1 C 1 D 1 is placed in the coordinate system so that the x, y and z axes are directed along the edges AB, AD and AA 1, respectively, and the origin coincides with point A. Point K is the midpoint of the edge A 1 B one . Find the coordinates of this point.
Since point K is the midpoint of the segment A 1 B 1, its coordinates are equal to the arithmetic mean of the coordinates of the ends. Let's write down the coordinates of the ends: A 1 = (0; 0; 1) and B 1 = (1; 0; 1). Now let's find the coordinates of point K:
Task. The unit cube ABCDA 1 B 1 C 1 D 1 is placed in the coordinate system so that the x, y and z axes are directed along the edges AB, AD and AA 1, respectively, and the origin coincides with point A. Find the coordinates of the point L where they intersect diagonals of the square A 1 B 1 C 1 D 1.
It is known from the planimetry course that the intersection point of the diagonals of a square is equidistant from all its vertices. In particular, A 1 L = C 1 L, i.e. point L is the midpoint of segment A 1 C 1. But A 1 = (0; 0; 1), C 1 = (1; 1; 1), so we have:
Answer: L = (0.5; 0.5; 1)
Geometry lesson in grade 11
Topic: " Method of coordinates in space ".
Target: To check the theoretical knowledge of students, their skills and abilities to apply this knowledge in solving problems using vector, vector-coordinate methods.
Tasks:
1 .Create conditions for control (self-control, mutual control) for the assimilation of knowledge and skills.
2. Develop mathematical thinking, speech, attention.
3. Promote activity, mobility, communication skills, general culture of students.
Form of conducting: work in groups.
Equipment and information sources: screen, multimedia projector, knowledge accounting table, credit cards, tests.
During the classes
1 mobilizing moment.
Lesson using CSR; students are divided into 3 dynamic groups, in which students with acceptable, optimal and advanced levels. In each group, a coordinator is selected who leads the work of the entire group.
2 ... Self-determination of students based on anticipation.
Task:goal setting according to the scheme: remember - learn - be able to.
Entrance Test - Fill in the blanks (in printouts)
Entrance test
Fill the gaps…
1.Three pairwise perpendicular lines are drawn through a point in space.
are selected, on each of them the direction and unit of measurement of the segments are selected,
then they say that it is set …………. in space.
2. Straight lines with directions chosen on them are called …………… ..,
and their common point is …………. ...
3. In a rectangular coordinate system, each point M in space is associated with a triplet of numbers that call it ……………… ..
4. The coordinates of a point in space are called ……………… ..
5. A vector whose length is equal to one is called ………… ..
6. Vectors iykare called ………….
7. Odds xyz in decomposition a= xi + yj + zk called
…………… vectors a .
8. Each coordinate of the sum of two or more vectors is equal to …………… ..
9. Each coordinate of the difference of two vectors is equal to ……………….
10. Each coordinate of the product of a vector and a number is equal to ……………… ..
11.Each coordinate of the vector is equal to …………….
12. Each coordinate of the segment midpoint is equal to ……………….
13. Vector length a { xyz) is calculated by the formula ……………………
14. Distance between points М 1 (x 1 ; y 1; z 1) and M 2 (x 2; y 2 ; z2) calculated by the formula …………………
15. The scalar product of two vectors is called …………… ..
16. The scalar product of nonzero vectors is equal to zero ……………… ..
17. Dot product of vectorsa{ x 1; y 1; z 1} b { x 2 ; y 2 ; z 2) in is expressed by the formula …………………
Cross-check of the input test. Answers to test tasks on the screen.
Evaluation criteria:
1-2 errors - "5"
3-4 errors - "4"
5-6 errors - "3"
In other cases - "2"
3. Execution of work. (by cards).
Each card contains two tasks: No. 1 - theoretical with proof, No. 2 includes tasks.
Explain the level of complexity of the tasks included in the work. The group performs one task, but having 2 parts. A group coordinator leads the work of the entire group. Discussion of one information with several partners increases responsibility not only for their own successes, but also for the results of collective work, which has a positive effect on the microclimate in the team.
CARD # 1
1. Derive formulas expressing the coordinates of the midpoint of a segment in terms of the coordinates of its ends.
2.Problem: 1) Given points A (-3; 1; 2) and B (1; -1; 2)
Find:
a) coordinates of the middle of the segment AB
b) coordinates and length of vector AB
2) Given a cube ABSDA1 B1 C1 D1. Using the coordinate method find the angle
between straight lines AB1 and A1 D.
CARD # 2
Output the formula for calculating the length of a vector by its coordinates.
Problem: 1) Given points M (-4; 7; 0),N(0; -1; 2). Find the distance from the origin to the midpoint of the segment MN.
→ → → → →
2) Given vectors a and b... Find b (a + b), if a (-2; 3; 6), b = 6i-8k
CARD # 3
Output a formula for calculating the distance between points with given coordinates.
Problem: 1) Given points A (2; 1; -8), B (1; -5; 0), C (8; 1; -4).
Prove that ∆ABC is isosceles and find the length of the midline of the triangle connecting the midpoints of the lateral sides.
2) Calculate the angle between straight lines AB and SD, if A (1; 1; 0),
B (3; -1; 2), D (0; 1; 0).
CARD # 4
Output the formulas for the cosine of the angle between nonzero vectors with the given coordinates.
Problem: 1) The coordinates of the three vertices of the AVSD parallelogram are given:
A (-6; -; 4; 0), B (6; -6; 2), C (10; 0; 4). Find the coordinates of point D.
2) Find the angle between straight lines AB and SD, if A (1; 1; 2), B (0; 1; 1), C (2; -2; 2), D (2; -3; 1).
CARD # 5
Tell me how to calculate the angle between two lines in space using the direction vectors of these lines. →→
Problem: 1) Find the dot product of vectorsa and b, if:
→ → → ^ →
a) | a| =4; | b| =√3 (ab)=30◦
b) a {2 ;-3; 1}, b = 3 i +2 k
2) Points A (0; 4; 0), B (2; 0; 0), C (4; 0; 4) and D (2; 4; 4) are given. Prove that AVSD is a rhombus.
4. Checking the work of dynamic groups by cards.
We listen to the performance of the representatives of the groups. The work of the groups is evaluated by the teacher with the participation of the students.
5. Reflection. Grades for offset.
Final multiple choice test (printouts).
1) Given vectors a {2 ;-4 ;3} b(-3; ─; 1). Find the coordinates of the vector
→ 2
c = a+ b
a) (-5; 3 -; 4); b) (-1; -3.5; 4) c) (5; -4 -; 2) d) (-1; 3.5; -4)
2) Given vectors a(4; -3; 5) and b(-3; 1; 2). Find the coordinates of the vector
C=2 a – 3 b
a) (7; -2; 3); b) (11; -7; 8); c) (17; -9; 4); d) (-1; -3; 4).
→ → → → → →
3) Calculate the dot product of the vectorsm and n, if m = a + 2 b- c
→ → → → →^ → → → → →
n= 2 a - b if | a|=2 , | b |=3, (ab) = 60 °, c ┴ a , c ┴ b.
a) -1; b) -27; in 1; d) 35.
4) Vector length a { xyz) is equal to 5. Find the coordinates of the vector a, ifx=2, z=-√5
a) 16; b) 4 or -4; at 9; d) 3 or -3.
5) Find the area ∆ABS, if A (1; -1; 3); B (3; -1; 1) and C (-1; 1; -3).
a) 4√3; b) √3; c) 2√3; d) √8.
Cross-check of the test. Answer codes for test items on the screen: 1 (b); 2 (c);
3 (a); 4 (b); 5 (c).
Evaluation criteria:
Everything is correct- "5"
1 error - "4"
2 errors - "3"
In other cases - "2"
Student knowledge table
Work on
cards
The final
test
Score for pass
Tasks
theory
practice
1st group
2nd group
Group 3
Assessment of student preparation for credit.
To use the preview of presentations, create yourself a Google account (account) and log into it: https://accounts.google.com
Slide captions:
Rectangular coordinate system in space. Vector coordinates.
Rectangular coordinate system
If three pairwise perpendicular straight lines are drawn through a point in space, on each of them a direction is chosen and a unit of measurement of segments is chosen, then they say that a rectangular coordinate system in space is given
The straight lines with the directions chosen on them are called the coordinate axes, and their common point is the origin. It is usually denoted by the letter O. The coordinate axes are designated as follows: Ox, Oy, O z - and have names: abscissa axis, ordinate axis, applicate axis.
The entire coordinate system is denoted by Oxy z. The planes passing through the coordinate axes Ox and Oy, Oy and O z, O z and Ox, respectively, are called coordinate planes and are denoted by Oxy, Oy z, O z x.
Point O divides each of the coordinate axes into two rays. A ray whose direction coincides with the direction of the axis is called the positive semiaxis, and the other ray the negative semiaxis.
In a rectangular coordinate system, each point M in space is associated with a triplet of numbers, which are called its coordinates.
The figure shows six points A (9; 5; 10), B (4; -3; 6), C (9; 0; 0), D (4; 0; 5), E (0; 3; 0) , F (0; 0; -3).
Vector coordinates
Any vector can be expanded in coordinate vectors, that is, represented in the form where the expansion coefficients x, y, z are uniquely determined.
The coefficients x, y and z in the expansion of the vector in coordinate vectors are called the coordinates of the vector in the given coordinate system.
Consider the rules that allow finding the coordinates of their sum and difference, as well as the coordinates of the product of a given vector by a given number, by the coordinates of these vectors.
10 . Each coordinate of the sum of two or more vectors is equal to the sum of the corresponding coordinates of these vectors. In other words, if a (x 1, y 1, z 1) and b (x 2, y 2, z 2) are these vectors, then the vector a + b has coordinates (x 1 + x 2, y 1 + y 2 , z 1 + z 2).
twenty . Each coordinate of the difference of two vectors is equal to the difference of the corresponding coordinates of these vectors. In other words, if a (x 1, y 1, z 1) and b (x 2 y 2; z 2) are these vectors, then the vector a - b has coordinates (x 1 - x 2, y 1 - y 2, z 1 - z 2).
thirty . Each coordinate of the product of a vector by a number is equal to the product of the corresponding coordinate of the vector by this number. In other words, if a (x; y; x) is a given vector, α is a given number, then the vector α a has coordinates (αх; αу; α z).
On the subject: methodological developments, presentations and notes
Didactic handout "A set of abstracts for students on the topic" Method of coordinates in space "for conducting lessons in the form of lectures. Geometry 10-11 grade ....
The purpose of the lesson: To check the knowledge, skills and abilities of students on the topic "Using the method of coordinates in space to solve tasks C2 of the exam". Planned educational results: Students demonstrate: ...
