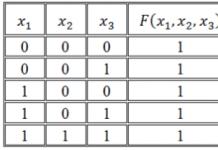
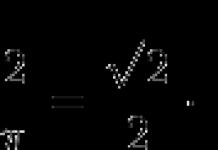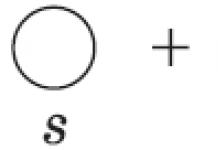DÉFINITION
Les inégalités trigonométriques sont des inégalités qui contiennent une variable sous le signe d'une fonction trigonométrique.
Résoudre les inégalités trigonométriques
Résoudre des inégalités trigonométriques revient souvent à résoudre les inégalités trigonométriques les plus simples de la forme : \(\ \sin x a \), \(\ \cos x > a \), \(\ \operatorname(tg) x > a \), \(\ \ nom de l'opérateur(ctg) x > a \), \(\ \sin x \leq a \), \(\ \cos x \leq a \), \(\ \nom de l'opérateur(tg) x \leq a \), \ (\ \operatorname(ctg) x \leq a \), \(\ \sin x \geq a \), \(\ \cos \geq a \), \(\ \operatorname(tg) x \geq a \ ), \(\ \operatorname(tg) x \geq a \)
Les inégalités trigonométriques les plus simples sont résolues graphiquement ou à l'aide du cercle trigonométrique unitaire.
Par définition, le sinus de l'angle \(\\alpha \) est l'ordonnée du point \(\P_(\alpha)(x, y)\) du cercle unité (Fig. 1), et le cosinus est l'abscisse de ce point. Ce fait est utilisé pour résoudre des inégalités trigonométriques simples avec cosinus et sinus en utilisant le cercle unité.
Exemples de résolution d'inégalités trigonométriques
Résoudre l'inégalité \(\ \sin x \leq \frac(\sqrt(3))(2) \)
Puisque \(\ \left|\frac(\sqrt(3))(2)\right| , alors cette inégalité a une solution et peut être résolue de deux manières
Première façon. Résolvons cette inégalité graphiquement. Pour ce faire, construisons un graphique du sinus \(\ y=\sin x \) (Fig. 2) et de la droite \(\ y=\frac(\sqrt(3))(2) \) dans un système de coordonnées
Soulignons les intervalles auxquels la sinusoïde se situe sous le graphique de la droite \(\ y=\frac(\sqrt(3))(2) \) . Trouvons les abscisses \(\ x_(1) \) et \(\ x_(2) \) des points d'intersection de ces graphiques : \(\ x_(1)=\pi-\arcsin \frac(\sqrt( 3))(2 )=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_(2)=\arcsin \frac(\sqrt(3))(2)+ 2 \pi=\ frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)
Nous avons l'intervalle \(\ \left[-\frac(4 \pi)(3) ; \frac(\pi)(3)\right] \) mais puisque la fonction \(\ y=\sin x \) est périodique et a un point \(\ 2 \pi \) , alors la réponse sera une union d'intervalles : \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac( 7 \pi)(3)+ 2 \pi k\right]\), \(\k \in Z\)
Deuxième façon. Construisons un cercle unité et une droite \(\ y=\frac(\sqrt(3))(2) \), leurs points d'intersection seront notés \(\ P_(x_(1)) \) et \ (\ P_(x_(2 )) \) (Fig. 3). La solution à l'inégalité d'origine sera l'ensemble des points d'ordonnées inférieurs à \(\ \frac(\sqrt(3))(2) \) . Trouvons la valeur de \(\ \boldsymbol(I)_(1) \) et \(\ \boldsymbol(I)_(2) \) en faisant le tour dans le sens inverse des aiguilles d'une montre, \(\ x_(1) Fig. 3
\(\ x_(1)=\pi-\arcsin \frac(\sqrt(3))(2)=\pi-\frac(\pi)(3)=\frac(2 \pi)(3) x_ (2)=\arcsin \frac(\sqrt(3))(2)+2 \pi=\frac(\pi)(3)+2 \pi=\frac(7 \pi)(3) \)
En tenant compte de la périodicité de la fonction sinus, on obtient finalement les intervalles \(\ \left[\frac(2 \pi)(3)+2 \pi k ; \frac(7 \pi)(3)+2 \ pi\right] \), \(\k\in Z\)
Résoudre l'inégalité \(\ \sin x>2\)
Le sinus est une fonction bornée : \(\ |\sin x| \leq 1 \) , et le côté droit de cette inégalité est supérieur à un, il n'y a donc pas de solutions.
Résoudre l'inégalité \(\ \cos x>\frac(1)(2) \)
Cette inégalité peut être résolue de deux manières : graphiquement et en utilisant le cercle unité. Considérons chacune des méthodes.
Première façon. Représentons dans un système de coordonnées les fonctions qui décrivent les côtés gauche et droit de l'inégalité, c'est-à-dire \(\ y=\cos x \) et \(\ y=\frac(1)(2) \) . Soulignons les intervalles où le graphe de la fonction cosinus \(\ y=\cos x \) se situe au-dessus du graphe de la droite \(\ y=\frac(1)(2) \) (Fig. 4 ).
Trouvons les abscisses des points \(\ \boldsymbol(x)_(1) \) et \(\ x_(2) \) – les points d'intersection des graphiques des fonctions \(\ y=\cos x \) et \(\ y=\frac (1)(2) \) , qui sont les extrémités de l'un des intervalles sur lesquels l'inégalité indiquée est vraie. \(\x_(1)=-\arccos \frac(1)(2)=-\frac(\pi)(3)\); \(\ x_(1)=\arccos \frac(1)(2)=\frac(\pi)(3) \)
Considérant que le cosinus est une fonction périodique, de point \(\ 2 \pi \) , la réponse sera les valeurs \(\ x \) des intervalles \(\ \left(-\frac(\pi) (3)+2 \pi k ; \frac(\pi)(3)+2 \pi k\right) \), \(\ k \in Z \)
Deuxième façon. Construisons un cercle unité et une droite \(\x=\frac(1)(2)\) (puisque cercle unitaire L'axe des abscisses correspond aux cosinus). Notons \(\ P_(x_(1)) \) et \(\ P_(x_(2)) \) (Fig. 5) – les points d'intersection de la droite et du cercle unité. La solution de l’équation d’origine sera l’ensemble des points d’abscisse inférieurs à \(\ \frac(1)(2) \) . Trouvons la valeur de \(\ x_(1) \) et \(\ 2 \) en faisant le tour dans le sens inverse des aiguilles d'une montre pour que \(\ x_(1) Compte tenu de la périodicité du cosinus, on obtient finalement les intervalles \( \ \left(-\frac (\pi)(3)+2 \pi k ; \frac(\pi)(3)+2 \pi k\right) \),\(\k \in Z\)
Résoudre l'inégalité \(\ \operatorname(ctg) x \leq-\frac(\sqrt(3))(3) \)
Construisons des graphiques des fonctions \(\ y=\operatorname(ctg) x \), \(\ y=-\frac(\sqrt(3))(3) \) dans un système de coordonnées
Soulignons les intervalles dans lesquels le graphique de la fonction \(\ y=\operatorname(ctg) x \) ne se situe pas plus haut que le graphique de la droite \(\ y=-\frac(\sqrt(3) )(3) \) (Fig. 6) .
Trouvons l'abscisse du point \(\ x_(0) \) , qui est la fin d'un des intervalles sur lesquels l'inégalité \(\ x_(0)=\operatorname(arcctg)\left(-\frac( \sqrt(3))( 3)\right)=\pi-\operatorname(arcctg)\left(\frac(\sqrt(3))(3)\right)=\pi-\frac(\pi)( 3)=\frac(2 \pi)(3)\)
L'autre extrémité de cet intervalle est le point \(\ \pi \) , et la fonction \(\ y=\operatorname(ctg) x \) à ce stade n'est pas définie. Ainsi, une des solutions à cette inégalité est l’intervalle \(\ \frac(2 \pi)(3) \leq x
Inégalités trigonométriques avec argument complexe
Les inégalités trigonométriques avec des arguments complexes peuvent être réduites à de simples inégalités trigonométriques par substitution. Après l'avoir résolu, la substitution inverse est effectuée et l'inconnue d'origine est exprimée.
Résoudre l'inégalité \(\ 2 \cos \left(2 x+100^(\circ)\right) \leq-1 \)
Exprimons le cosinus du côté droit de cette inégalité : \(\ \cos \left(2 x+100^(\circ)\right) \leq-\frac(1)(2) \)
Nous effectuons le remplacement \(\ t=2 x+100^(\circ) \) , après quoi cette inégalité est transformée en l'inégalité la plus simple \(\ \cos t \leq-\frac(1)(2) \)
Résolvons-le en utilisant le cercle unité. Construisons un cercle unité et une droite \(\ x=-\frac(1)(2) \) . Notons \(\P_(1)\) et \(\P_(2)\) – les points d'intersection de la droite et du cercle unité (Fig. 7).
La solution de l'inégalité d'origine sera l'ensemble des points d'abscisse, dont il n'y a pas plus de \(\ -\frac(1)(2)\). Le point \(\ P_(1) \) correspond à l'angle \(\ 120^(\circ) \) , et le point \(\ P_(2) \) . Ainsi, en tenant compte de la période du cosinus, on obtient \(\ 120^(\circ)+360^(\circ) \cdot n \leq t \leq 240^(\circ)+360^(\circ) \cdot n \) ,\(\n\in Z\)
Faisons le changement inverse \(\ t=2 x+100^(\circ) 120^(\circ)+360^(\circ) \cdot n \leq 2 x+100^(\circ) \leq 240^ (\ circ)+360^(\circ) \cdot n\), \(\n \in Z\)
Exprimons \(\ \mathbf(x) \), pour soustraire d'abord \(\ 100^(\circ) 120^(\circ) -100^(\circ)+360^(\circ) \ cdot n \ leq 2 x+100^(\circ)-100^(\circ) \leq 240^(\circ)-100^(\circ)+360^(\circ) \cdot n \), \( \n\ dans Z\); \(\ 20^(\circ)+360^(\circ) \cdot n \leq 2 x \leq 140^(\circ)+360^(\circ) \cdot n \), \(\ n \in Z\)
puis divisez par 2 \(\ \frac(20^(\circ)+360^(\circ) \cdot n)(2) \leq \frac(2 x)(2) \leq \frac(140^ (\circ)+360^(\circ) \cdot n)(2) \), \(\n \in Z\); \(\ 10^(\circ)+180^(\circ) \cdot n \leq x \leq 70^(\circ)+180^(\circ) \cdot n \), \(\ n \in Z \)
Inégalités trigonométriques doubles
Résoudre la double inégalité trigonométrique \(\ \frac(1)(2)
Introduisons le remplacement \(\ t=\frac(x)(2) \) , alors l'inégalité originale prendra la forme \(\ \frac(1)(2)
Résolvons-le en utilisant le cercle unité. Puisque sur le cercle unité le sinus correspond à l'axe des ordonnées, on y sélectionne un ensemble d'ordonnées dont les ordonnées sont supérieures à \(\ x=\frac(1)(2) \) et inférieures ou égales à \(\ \frac(\sqrt(2))(2 ) \) . Sur la figure 8, ces points seront situés sur les arcs \(\P_(t_(1))\), \(\P_(t_(2))\) et \(\P_(t_(3))\) , \( \P_(t_(4))\) . Trouvons la valeur \(\ t_(1) \), \(\ t_(2) \), \(\ t_(3) \), \(\ t_(4) \) en faisant le tour dans le sens inverse des aiguilles d'une montre, et \ (\t_(1)\(\t_(3)=\pi-\arcsin \frac(\sqrt(2))(2)=\pi-\frac(\pi)(4)=\frac(3\ pi)(4) \);\(\ t_(4)=\pi-\arcsin \frac(1)(2)=\pi-\frac(\pi)(6)=\frac(5 \pi) (6)\)
Ainsi, on obtient deux intervalles, qui, compte tenu de la périodicité de la fonction sinus, peuvent s'écrire comme suit \(\ \frac(\pi)(6)+2 \pi k \leq t \frac(\pi) (4)+2 \ pi k \quad \frac(3 \pi)(4)+2 \pi k Faisons le changement inverse \(\ t=\frac(x)(2) \frac(\pi)( 6)+2 \pi k \ leq \frac(x)(2) \frac(\pi)(4)+2 \pi k \), \(\ \frac(3 \pi)(4)+2 \ pi k Exprimons \(\ \mathbf( x) \), pour cela, multiplions tous les côtés des deux inégalités par 2, on obtient \(\ \frac(\pi)(3)+4 \pi k \leq X
Ministère de l'Éducation de la République de Biélorussie
Établissement d'enseignement
"Université d'État de Gomel
nommé d'après Francysk Skaryna"
Faculté de Mathématiques
Département d'algèbre et de géométrie
Accepté pour la défense
Tête Département Shemetkov L.A.
Équations trigonométriques et inégalités
Travaux de cours
Exécuteur:
élève du groupe M-51
CM. Gorski
Directeur scientifique Ph.D.-M.Sc.,
Maître de conférences
V.G. Safonov
Homiel 2008
INTRODUCTION
MÉTHODES DE BASE POUR RÉSOUDRE DES ÉQUATIONS TRIGONOMÉTRIQUES
Factorisation
Résoudre des équations en convertissant le produit de fonctions trigonométriques en une somme
Résoudre des équations à l'aide de formules à triple argument
Multiplication par une fonction trigonométrique
ÉQUATIONS TRIGONOMÉTRIQUES NON STANDARD
INÉGALITÉS TRIGONOMÉTRIQUES
SÉLECTION DES RACINES
TÂCHES POUR UNE SOLUTION INDÉPENDANTE
CONCLUSION
LISTE DES SOURCES UTILISÉES
Dans les temps anciens, la trigonométrie est née en relation avec les besoins de l'astronomie, de l'arpentage et de la construction, c'est-à-dire qu'elle était de nature purement géométrique et représentait principalement<<исчисление хорд>>. Au fil du temps, certains moments analytiques ont commencé à s’y intercaler. Dans la première moitié du XVIIIe siècle, il y a eu un changement radical, après quoi la trigonométrie a pris une nouvelle direction et s'est orientée vers l'analyse mathématique. C’est à cette époque que les relations trigonométriques commencent à être considérées comme des fonctions.
Les équations trigonométriques sont l'un des sujets les plus difficiles cours scolaire mathématiques. Les équations trigonométriques surviennent lors de la résolution de problèmes de planimétrie, de stéréométrie, d'astronomie, de physique et d'autres domaines. Les équations trigonométriques et les inégalités font partie des missions année après année tests centralisés.
La différence la plus importante entre les équations trigonométriques et les équations algébriques réside dans le fait que les équations algébriques ont un nombre fini de racines, tandis que les équations trigonométriques --- infini, ce qui complique grandement la sélection des racines. Une autre particularité des équations trigonométriques est la forme non unique d’écriture de la réponse.
Cette thèse est consacrée aux méthodes de résolution d'équations trigonométriques et d'inégalités.
La thèse comprend 6 sections.
La première section fournit des informations théoriques de base : définition et propriétés des fonctions trigonométriques et trigonométriques inverses ; tableau des valeurs des fonctions trigonométriques pour certains arguments ; exprimer des fonctions trigonométriques en termes d'autres fonctions trigonométriques, ce qui est très important pour transformer des expressions trigonométriques, notamment celles contenant des fonctions trigonométriques inverses ; sauf les principaux formules trigonométriques, bien connues du cours scolaire, des formules sont données pour simplifier des expressions contenant des fonctions trigonométriques inverses.
La deuxième section décrit les méthodes de base pour résoudre des équations trigonométriques. La solution des équations trigonométriques élémentaires, la méthode de factorisation et les méthodes de réduction des équations trigonométriques aux équations algébriques sont considérées. En raison du fait que les solutions des équations trigonométriques peuvent être écrites de plusieurs manières et que la forme de ces solutions ne permet pas de déterminer immédiatement si ces solutions sont identiques ou différentes, ce qui peut<<сбить с толку>> lors de la résolution des tests, le schéma général de résolution des équations trigonométriques a été pris en compte et la transformation des groupes a été examinée en détail solutions généraleséquations trigonométriques.
La troisième section examine des équations trigonométriques non standard dont les solutions sont basées sur l'approche fonctionnelle.
La quatrième section traite des inégalités trigonométriques. Les méthodes de résolution des inégalités trigonométriques élémentaires, tant sur le cercle unité que par la méthode graphique, sont discutées en détail. Le processus de résolution des inégalités trigonométriques non élémentaires par les inégalités élémentaires et la méthode des intervalles, déjà bien connue des écoliers, est décrit.
La cinquième section présente les tâches les plus difficiles : lorsqu'il est nécessaire non seulement de résoudre une équation trigonométrique, mais également de sélectionner parmi les racines trouvées des racines qui satisfont à certaines conditions. Cette section fournit des solutions aux tâches typiques de sélection de racine. Les informations théoriques nécessaires à la sélection des racines sont données : partitionnement d'un ensemble d'entiers en sous-ensembles disjoints, résolution d'équations en entiers (diaphantine).
La sixième section présente les tâches de décision indépendante, conçu sous la forme d’un test. Les 20 tâches de test contiennent les tâches les plus difficiles pouvant être rencontrées lors de tests centralisés.
Équations trigonométriques élémentaires
Les équations trigonométriques élémentaires sont des équations de la forme , où --- une des fonctions trigonométriques : , , , .
Les équations trigonométriques élémentaires ont un nombre infini de racines. Par exemple, les valeurs suivantes satisfont l'équation : , , , etc. La formule générale par laquelle toutes les racines de l'équation sont trouvées, où , est la suivante :
Ici, il peut prendre n'importe quelle valeur entière, chacune d'elles correspond à une racine spécifique de l'équation ; dans cette formule (ainsi que dans d'autres formules par lesquelles les équations trigonométriques élémentaires sont résolues) sont appelés paramètre. Ils écrivent généralement , soulignant ainsi que le paramètre peut accepter n'importe quelle valeur entière.
Les solutions de l'équation , où , sont trouvées par la formule
L'équation est résolue à l'aide de la formule
et l'équation est par la formule
Notons surtout quelques cas particuliers d'équations trigonométriques élémentaires, où la solution peut être écrite sans utiliser de formules générales :
Lors de la résolution d'équations trigonométriques, la période des fonctions trigonométriques joue un rôle important. Par conséquent, nous présentons deux théorèmes utiles :
Théorème Si --- la période principale de la fonction, alors le nombre est la période principale de la fonction.
Les périodes des fonctions et sont dites commensurables s'il existe entiers Et alors .
Théorème Si les fonctions périodiques et , ont des et , alors elles ont une période commune, qui est la période des fonctions , , .
Le théorème stipule que la période de la fonction , , , est et n'est pas nécessairement la période principale. Par exemple, la période principale des fonctions et --- , et la période principale de leur produit --- .
Introduction d'un argument auxiliaire
Par la manière standard de transformer les expressions de la forme 
est la technique suivante : soit --- coin, donné par les égalités 
, 
. Pour tout le monde, un tel angle existe. Ainsi . Si , ou , , , dans les autres cas.
Schéma de résolution d'équations trigonométriques
Le schéma de base que nous suivrons lors de la résolution d’équations trigonométriques est le suivant :
solution équation donnée revient à résoudre des équations élémentaires. La solution signifie : transformations, factorisation, remplacement d'inconnues. Le principe directeur est de ne pas perdre ses racines. Cela signifie que lorsque nous passons à la ou aux équations suivantes, nous n'avons pas peur de l'apparition de racines supplémentaires (externes), mais nous nous soucions seulement que chaque équation suivante de notre « chaîne » (ou un ensemble d'équations dans le cas de branchements) ) est une conséquence du précédent. Une méthode possible pour sélectionner les racines est le test. Notons tout de suite que dans le cas des équations trigonométriques, les difficultés liées à la sélection des racines et à la vérification, en règle générale, augmentent fortement par rapport aux équations algébriques. Après tout, nous devons vérifier des séries constituées d’un nombre infini de termes.
Une mention spéciale doit être faite au remplacement des inconnues lors de la résolution d'équations trigonométriques. Dans la plupart des cas, après la substitution nécessaire, une équation algébrique est obtenue. De plus, il n'est pas si rare que des équations qui, bien que trigonométriques en apparence, ne soient pas essentiellement trigonométriques, puisqu'après la première étape --- remplacements les variables --- se transforment en variables algébriques, et le retour à la trigonométrie ne se produit qu'au stade de la résolution des équations trigonométriques élémentaires.
Rappelons encore une fois : le remplacement de l'inconnue doit être effectué à la première occasion ; l'équation résultante après le remplacement doit être résolue jusqu'au bout, y compris l'étape de sélection des racines, et ensuite seulement renvoyée à l'inconnue d'origine.
L’une des caractéristiques des équations trigonométriques est que la réponse peut, dans de nombreux cas, être écrite de différentes manières. Même pour résoudre l'équation 
la réponse peut s'écrire comme suit :
1) sous forme de deux séries : 
, , ;
2) sous forme standard, qui est une combinaison des séries ci-dessus : , ;
3) parce que 
, alors la réponse peut s'écrire sous la forme 
, . (Dans ce qui suit, la présence du paramètre , ou dans l'enregistrement de réponse signifie automatiquement que ce paramètre accepte toutes les valeurs entières possibles. Des exceptions seront spécifiées.)
Evidemment, les trois cas listés n'épuisent pas toutes les possibilités d'écriture de la réponse à l'équation considérée (il y en a une infinité).
Par exemple, lorsque l'égalité est vraie 
. Ainsi, dans les deux premiers cas, si , on peut remplacer par .
Habituellement, la réponse est écrite sur la base du point 2. Il est utile de rappeler la recommandation suivante : si le travail ne se termine pas par la résolution de l'équation, il faut quand même mener des recherches et sélectionner les racines, alors la forme d'enregistrement la plus pratique est indiqué au point 1. (Une recommandation similaire devrait être donnée pour l’équation.)
Prenons un exemple illustrant ce qui a été dit.
Exemple Résous l'équation.
Solution. La manière la plus évidente est la suivante. Cette équation se décompose en deux : et . En résolvant chacun d'eux et en combinant les réponses obtenues, nous trouvons .
Autrement. Depuis , remplacez et utilisez les formules de réduction du degré. Après de petites transformations on obtient , d'où 
.
A première vue, la seconde formule ne présente pas d’avantages particuliers par rapport à la première. Cependant, si nous prenons, par exemple, il s'avère que, c'est-à-dire l'équation a une solution, tandis que la première méthode nous amène à la réponse 
. "Voir" et prouver l'égalité 
pas si facile.
Répondre. .
Conversion et combinaison de groupes de solutions générales d'équations trigonométriques
Nous allons le prendre en compte progression arithmétique, s'étendant sans fin dans les deux sens. Les membres de cette progression peuvent être divisés en deux groupes de membres, situés à droite et à gauche d'un certain membre appelé membre central ou zéro de la progression.
En fixant l'un des termes d'une progression infinie avec un nombre nul, nous devrons effectuer une double numérotation pour tous les termes restants : positif pour les termes situés à droite, et négatif pour les termes situés à gauche de zéro.
En général, si la différence de la progression est le terme zéro, la formule pour tout (ième) terme d'une progression arithmétique infinie est :
Transformations de formules pour tout terme d'une progression arithmétique infinie
1. Si vous ajoutez ou soustrayez la différence de progression jusqu'au terme zéro, alors la progression ne changera pas, mais seul le terme zéro bougera, c'est-à-dire La numérotation des membres va changer.
2. Si le coefficient à variable multiplié par , cela n'entraînera qu'un réarrangement des groupes de membres de droite et de gauche.
3. Si les termes successifs d'une progression infinie
par exemple, , , ..., , faire en sorte que les termes centraux des progressions avec la même différence soient égaux à :
alors une progression et une série de progressions expriment les mêmes nombres.
Exemple La ligne peut être remplacée par les trois lignes suivantes : , , .
4. Si des progressions infinies avec même différence ont pour termes centraux des nombres qui forment une progression arithmétique avec différence, alors ces séries peuvent être remplacées par une progression avec différence, et avec un terme central égal à l'un des termes centraux de ces progressions, c'est à dire. Si
alors ces progressions sont combinées en une seule :
Exemple
... les deux sont combinés en un seul groupe, puisque 
.
Pour transformer des groupes ayant des solutions communes en groupes n'ayant pas de solutions communes, ces groupes sont décomposés en groupes avec période générale, puis efforcez-vous de combiner les groupes résultants, en éliminant ceux qui se répètent.
Factorisation
La méthode de factorisation est la suivante : si
alors chaque solution de l'équation
est la solution d'un ensemble d'équations
L’affirmation inverse est, d’une manière générale, fausse : toute solution à la population n’est pas nécessairement une solution à l’équation. Cela s'explique par le fait que les solutions d'équations individuelles peuvent ne pas être incluses dans le domaine de définition de la fonction.
Exemple Résous l'équation.
Solution. En utilisant l'identité trigonométrique de base, nous représentons l'équation sous la forme
Répondre.
; 
.
Conversion de la somme des fonctions trigonométriques en un produit
Exemple
Résous l'équation 
.
Solution. En appliquant la formule, on obtient l'équation équivalente
Répondre. .
Exemple Résous l'équation.
Solution. Dans ce cas, avant d'appliquer les formules de somme des fonctions trigonométriques, vous devez utiliser la formule de réduction 
. En conséquence, nous obtenons l'équation équivalente
Répondre.
, 
.
Résoudre des équations en convertissant le produit de fonctions trigonométriques en une somme
Lors de la résolution d'un certain nombre d'équations, des formules sont utilisées.
Exemple Résous l'équation
Solution.
Répondre. , .
Exemple Résous l'équation.
Solution. En appliquant la formule, on obtient une équation équivalente :
Répondre. .
Résoudre des équations à l'aide de formules de réduction
Lors de la résolution d'un large éventail d'équations trigonométriques, les formules jouent un rôle clé.
Exemple Résous l'équation.
Solution. En appliquant la formule, nous obtenons une équation équivalente.
Répondre. ; .
Résoudre des équations à l'aide de formules à triple argument
Exemple Résous l'équation.
Solution. En appliquant la formule, on obtient l'équation
Répondre. ; .
Exemple
Résous l'équation 
.
Solution. En appliquant les formules de réduction du degré, nous obtenons : 
. En postulant, nous obtenons :
Répondre. ; .
Égalité des fonctions trigonométriques du même nom
Exemple Résous l'équation.
Solution.
Répondre. , .
Exemple
Résous l'équation 
.
Solution. Transformons l'équation.
Répondre. .
Exemple On sait que et satisfont l'équation
Trouvez le montant.
Solution. De l'équation il résulte que
Répondre. .
Considérons des sommes de la forme
Ces montants peuvent être convertis en produit en les multipliant et en les divisant par, on obtient alors
Cette technique peut être utilisée pour résoudre certaines équations trigonométriques, mais il convient de garder à l'esprit qu'en conséquence, des racines superflues peuvent apparaître. Résumons ces formules :
Exemple Résous l'équation.
Solution. On voit que l’ensemble est une solution de l’équation originale. Par conséquent, multiplier les côtés gauche et droit de l’équation par n’entraînera pas l’apparition de racines supplémentaires.
Nous avons 
.
Répondre. ; .
Exemple Résous l'équation.
Solution. Multiplions les côtés gauche et droit de l'équation par et appliquons les formules pour convertir le produit des fonctions trigonométriques en une somme, nous obtenons
Cette équation est équivalente à la combinaison de deux équations et , d'où et .
Puisque les racines de l’équation ne sont pas les racines de l’équation, nous devrions exclure . Cela signifie que dans l'ensemble il faut exclure .
Répondre. Et , .
Exemple
Résous l'équation 
.
Solution. Transformons l'expression :
L'équation s'écrira ainsi :
Répondre. .
Réduire les équations trigonométriques aux équations algébriques
Réductible au carré
Si l'équation est de la forme
alors le remplacement le conduit au carré, puisque 
() Et.
Si au lieu du terme il y a , alors le remplacement requis sera .
L'équation
revient à équation quadratique
présentation comme 
. Il est facile de vérifier ce pour quoi , ne sont pas des racines de l'équation, et en effectuant la substitution , l'équation se réduit à une équation quadratique.
Exemple Résous l'équation.
Solution. Déplaçons-le vers la gauche, remplaçons-le par et exprimons-le par et .
Après simplifications on obtient : . Divisez terme par terme et effectuez le remplacement :
En revenant à , nous trouvons 
.
Équations homogènes par rapport à ,
Considérons une équation de la forme
Où , , , ..., , --- valide Nombres. Dans chaque terme du côté gauche de l'équation, les degrés des monômes sont égaux, c'est-à-dire que la somme des degrés du sinus et du cosinus est la même et égale. Cette équation s'appelle homogène par rapport à et , et le numéro est appelé indicateur d'homogénéité .
Il est clair que si , alors l'équation prendra la forme :
dont les solutions sont les valeurs auxquelles , c'est-à-dire les nombres , . La deuxième équation écrite entre parenthèses est également homogène, mais les degrés sont inférieurs de 1.
Si , alors ces nombres ne sont pas les racines de l’équation.
Quand on obtient : , et le côté gauche de l’équation (1) prend la valeur .
Ainsi, pour , et , nous pouvons donc diviser les deux côtés de l’équation par . En conséquence, nous obtenons l'équation :
qui, par substitution, peut facilement être réduit à l'algébrique :
Équations homogènes avec indice d'homogénéité 1. Quand on a l'équation .
Si , alors cette équation est équivalente à l'équation , , d'où , .
Exemple Résous l'équation.
Solution. Cette équation est homogène du premier degré. Divisez les deux parties par nous obtenons : , , , .
Répondre. .
Exemple Lorsqu'on obtient une équation homogène de la forme
Solution.
Si , alors divisez les deux côtés de l'équation par , nous obtenons l'équation 
, qui peut être facilement réduit au carré par substitution : 
. Si 
, alors l'équation a des racines réelles , . L'équation originale aura deux groupes de solutions : , , .
Si 
, alors l'équation n'a pas de solutions.
Exemple Résous l'équation.
Solution. Cette équation est homogène du deuxième degré. En divisant les deux côtés de l'équation par , nous obtenons : . Soit , alors , , . , , ; . . .
Répondre.
.
L'équation se réduit à une équation de la forme
Pour ce faire, il suffit d'utiliser l'identité 
En particulier, l'équation est réduite à homogène si on la remplace par 
, alors on obtient une équation équivalente :
Exemple Résous l'équation.
Solution. Transformons l'équation en une équation homogène :
Divisons les deux côtés de l'équation par 
, on obtient l'équation :
Soit , alors nous arrivons à l'équation quadratique : 
, , 
, 
, .
Répondre.
.
Exemple Résous l'équation.
Solution. Mettons au carré les deux côtés de l'équation, en tenant compte du fait qu'ils ont des valeurs positives : , ,
Laisse faire, alors nous obtenons 
, , .
Répondre. .
Équations résolues à l'aide d'identités 
Il est utile de connaître les formules suivantes :
Exemple Résous l'équation.
Solution. En utilisant, on obtient
Répondre.
Nous ne proposons pas les formules elles-mêmes, mais une méthode pour les dériver :
ainsi,
De même, .
Exemple
Résous l'équation 
.
Solution. Transformons l'expression :
L'équation s'écrira ainsi :
En acceptant, nous recevons. , . Ainsi
Répondre. .
Substitution trigonométrique universelle
Équation trigonométrique de la forme
Où --- rationnel une fonction à l'aide de formules - , ainsi qu'à l'aide de formules - peut être réduite à équation rationnelle par rapport aux arguments , , , , après quoi l'équation peut être réduite à une équation algébrique rationnelle en ce qui concerne l'utilisation des formules de substitution trigonométrique universelle
Il convient de noter que l'utilisation de formules peut conduire à un rétrécissement de la DO de l'équation d'origine, car elle n'est pas définie aux points. Dans de tels cas, il est donc nécessaire de vérifier si les angles sont les racines de l'équation d'origine. .
Exemple Résous l'équation.
Solution. Selon les conditions de la tâche. En appliquant les formules et en effectuant la substitution, on obtient
d'où et donc.
Équations de la forme
Équations de la forme , où --- polynôme, sont résolus en utilisant des remplacements d'inconnues
Exemple Résous l'équation.
Solution. En effectuant le remplacement et en prenant en compte cela, nous obtenons
où , . --- racine étrangère, parce que . Racines de l'équation 
sont .
Utilisation des limitations des fonctionnalités
Dans la pratique des tests centralisés, il n'est pas si rare de rencontrer des équations dont la solution repose sur les fonctions limitées et . Par exemple:
Exemple Résous l'équation.
Solution. Puisque , , alors le côté gauche n'excède pas et est égal à , si
Pour trouver des valeurs qui satisfont aux deux équations, nous procédons comme suit. Résolvons l'une d'elles, puis parmi les valeurs trouvées nous sélectionnerons celles qui satisfont l'autre.
Commençons par le deuxième : , . Alors , 
.
Il est clair qu'il n'y en aura que pour les nombres pairs.
Répondre. .
Une autre idée est réalisée en résolvant l’équation suivante :
Exemple
Résous l'équation 
.
Solution. Utilisons la propriété fonction exponentielle: , 
.
En additionnant ces inégalités terme par terme on a :
Par conséquent, le côté gauche de cette équation est égal si et seulement si deux égalités sont satisfaites :
c'est-à-dire qu'il peut prendre les valeurs , , , ou il peut prendre les valeurs , .
Répondre. , .
Exemple
Résous l'équation 
.
Solution., . Ainsi, 
.
Répondre. .
Exemple Résous l'équation
Solution. Notons , alors de la définition de la fonction trigonométrique inverse on a 
Et 
.
Puisque l'inégalité découle de l'équation, c'est-à-dire . Depuis et , puis et . Cependant, c'est pourquoi.
Si et, alors. Puisqu'il a été établi précédemment que , alors .
Répondre. , .
Exemple Résous l'équation
Solution. La plage des valeurs acceptables de l'équation est .
Montrons d’abord que la fonction
Pour toute personne, cela ne peut prendre que des valeurs positives.
Imaginons la fonction comme suit : .
Puisque , alors cela a lieu, c'est-à-dire 
.
Par conséquent, pour prouver l’inégalité, il faut montrer que 
. Pour cela, cubons les deux côtés de cette inégalité, puis
L'inégalité numérique qui en résulte indique que . Si nous prenons également en compte cela, alors le côté gauche de l’équation est non négatif.
Regardons maintenant le côté droit de l'équation.
Parce que 
, Que
Or, on sait que 
. Il s'ensuit que, c'est-à-dire le côté droit de l’équation ne dépasse pas . Il a été prouvé précédemment que le côté gauche de l’équation n’est pas négatif, donc l’égalité ne peut se produire que si les deux côtés sont égaux, et cela n’est possible que si .
Répondre. .
Exemple Résous l'équation
Solution. Notons et 
. En appliquant l'inégalité de Cauchy-Bunyakovsky, on obtient . Il s'ensuit que 
. D'un autre côté, il y a 
. L’équation n’a donc pas de racine.
Répondre. .
Exemple Résous l'équation:
Solution. Réécrivons l'équation comme suit :
Répondre. .
Méthodes fonctionnelles pour résoudre des équations trigonométriques et combinées
Toutes les équations résultant de transformations ne peuvent pas être réduites à une équation de l'une ou l'autre forme standard, pour laquelle il existe une méthode de résolution spécifique. Dans de tels cas, il s'avère utile d'utiliser des propriétés de fonctions telles que la monotonie, la limitation, la parité, la périodicité, etc. Ainsi, si l'une des fonctions diminue et la seconde augmente sur l'intervalle, alors si l'équation a un racine sur cet intervalle, cette racine est unique, et alors, par exemple, elle peut être trouvée par sélection. Si la fonction est limitée au-dessus, et , et que la fonction est limitée en dessous, et , alors l'équation est équivalente au système d'équations
Exemple Résous l'équation
Solution. Transformons l'équation originale sous la forme
et résolvez-le comme une quadratique par rapport à . Ensuite, nous obtenons,
Résolvons la première équation de la population. Compte tenu du caractère limité de la fonction, nous arrivons à la conclusion que l'équation ne peut avoir de racine que sur le segment. Sur cet intervalle la fonction augmente, et la fonction 
diminue. Par conséquent, si cette équation a une racine, alors elle est unique. Nous trouvons par sélection.
Répondre. .
Exemple Résous l'équation
Solution. Laissez et 
, alors l'équation originale peut être écrite sous forme d'équation fonctionnelle. Puisque la fonction est impaire, alors . Dans ce cas, nous obtenons l'équation.
Puisque , et est monotone sur , l'équation est équivalente à l'équation, c'est-à-dire 
, qui a une seule racine.
Répondre. .
Exemple
Résous l'équation 
.
Solution. Basé sur le théorème des dérivées fonction complexe il est clair que la fonction 
décroissant (fonction décroissante, croissante, décroissante). Il ressort clairement de là que la fonction 
défini sur , décroissant. Cette équation a donc au plus une racine. Parce que 
, Que
Répondre. .
Exemple Résous l'équation.
Solution. Considérons l'équation sur trois intervalles.
a) Soit . Alors sur cet ensemble, l'équation d'origine est équivalente à l'équation . Qui n'a pas de solutions sur l'intervalle, car 
, , UN . Sur l'intervalle, l'équation originale n'a pas non plus de racines, car 
, UN .
b) Soit . Alors sur cet ensemble l'équation d'origine est équivalente à l'équation
dont les racines sur l'intervalle sont les nombres , , , .
c) Soit . Alors sur cet ensemble l'équation d'origine est équivalente à l'équation
Ce qui n'a pas de solutions sur l'intervalle, car , et . Sur l'intervalle, l'équation n'a pas non plus de solutions, car , , UN .
Répondre. , , , .
Méthode de symétrie
La méthode de symétrie est pratique à utiliser lorsque la formulation du problème nécessite la solution unique d'une équation, d'une inégalité, d'un système, etc. ou une indication exacte du nombre de solutions. Dans ce cas, toute symétrie des expressions données doit être détectée.
Il faut également prendre en compte la variété des différents types de symétrie possibles.
Il est tout aussi important de respecter scrupuleusement les étapes logiques du raisonnement symétrique.
Typiquement, la symétrie permet d'établir uniquement les conditions nécessaires, puis il est nécessaire de vérifier leur suffisance.
Exemple Trouvez toutes les valeurs du paramètre pour lequel l'équation a une solution unique.
Solution. Noter que --- même fonctions, donc le côté gauche de l’équation est une fonction paire.
Donc si --- solutionéquations, c'est-à-dire également la solution de l'équation. Si --- la seule chose solution à l'équation, alors nécessaire , .
Nous sélectionnerons possible valeurs, exigeant que ce soit la racine de l’équation.
Notons tout de suite que d'autres valeurs ne peuvent satisfaire aux conditions du problème.
Mais on ne sait pas encore si tous les candidats sélectionnés satisfont réellement aux conditions du problème.
Adéquation.
1), l’équation prendra la forme 
.
2), l’équation prendra la forme :
Il est évident que, pour tout le monde et 
. La dernière équation est donc équivalente au système :
Ainsi, nous avons prouvé que pour , l’équation a une solution unique.
Répondre. .
Solution avec exploration de fonctions
Exemple Montrer que toutes les solutions de l'équation
Nombres entiers.
Solution. La période principale de l’équation originale est . Par conséquent, nous examinons d’abord cette équation sur l’intervalle.
Transformons l'équation sous la forme :
En utilisant une microcalculatrice on obtient :
Si , alors à partir des égalités précédentes on obtient :
Après avoir résolu l'équation résultante, nous obtenons : .
Les calculs effectués permettent de supposer que les racines de l'équation appartenant au segment, sont , et .
Les tests directs confirment cette hypothèse. Ainsi, il a été prouvé que les racines de l'équation ne sont que des nombres entiers , .
Exemple
Résous l'équation 
.
Solution. Trouvons la période principale de l'équation. La fonction a une période de base égale à . La période principale de la fonction est . Le plus petit commun multiple de et est égal à . La période principale de l’équation est donc . Laisser .
C’est évidemment une solution à l’équation. Sur l'intervalle. La fonction est négative. Par conséquent, les autres racines de l’équation ne doivent être recherchées que sur les intervalles x et .
A l'aide d'une microcalculatrice, on trouve d'abord les valeurs approximatives des racines de l'équation. Pour ce faire, nous compilons un tableau de valeurs de fonctions 
sur les intervalles et ; c'est-à-dire sur les intervalles et .
| 0 | 0 | 202,5 | 0,85355342 |
| 3 | -0,00080306 | 207 | 0,6893642 |
| 6 | -0,00119426 | 210 | 0,57635189 |
| 9 | -0,00261932 | 213 | 0,4614465 |
| 12 | -0,00448897 | 216 | 0,34549155 |
| 15 | -0,00667995 | 219 | 0,22934931 |
| 18 | -0,00903692 | 222 | 0,1138931 |
| 21 | -0,01137519 | 225 | 0,00000002 |
| 24 | -0,01312438 | 228 | -0,11145712 |
| 27 | -0,01512438 | 231 | -0,21961736 |
| 30 | -0,01604446 | 234 | -0,32363903 |
| 33 | -0,01597149 | 237 | -0,42270819 |
| 36 | -0,01462203 | 240 | -0,5160445 |
| 39 | -0,01170562 | 243 | -0,60290965 |
| 42 | -0,00692866 | 246 | -0,65261345 |
| 45 | 0,00000002 | 249 | -0,75452006 |
| 48 | 0,00936458 | 252 | -0,81805397 |
| 51 | 0,02143757 | 255 | -0,87270535 |
| 54 | 0,03647455 | 258 | -0,91803444 |
| 57 | 0,0547098 | 261 | -0,95367586 |
| 60 | 0,07635185 | 264 | -0,97934187 |
| 63 | 0,10157893 | 267 | -0,99482505 |
| 66 | 0,1305352 | 270 | -1 |
| 67,5 | 0,14644661 |
A partir du tableau, les hypothèses suivantes ressortent facilement : les racines de l'équation appartenant au segment sont les nombres : ; ; . Les tests directs confirment cette hypothèse.
Répondre.
; 
; .
Résoudre des inégalités trigonométriques à l'aide du cercle unité
Lors de la résolution d'inégalités trigonométriques de la forme , où est l'une des fonctions trigonométriques, il est pratique d'utiliser un cercle trigonométrique afin de représenter le plus clairement possible les solutions à l'inégalité et d'écrire la réponse. La principale méthode pour résoudre les inégalités trigonométriques est de les réduire aux inégalités de type les plus simples. Regardons un exemple de la façon de résoudre de telles inégalités.
Exemple Résolvez l’inégalité.
Solution. Traçons un cercle trigonométrique et marquons dessus les points dont l'ordonnée dépasse .
La solution à cette inégalité sera . Il est également clair que si un certain nombre diffère de n'importe quel nombre de l'intervalle spécifié de , alors il ne sera également pas inférieur à . Par conséquent, il vous suffit d’ajouter aux extrémités du segment de solution trouvée. Finalement, nous constatons que les solutions à l’inégalité originelle seront toutes 
.
Répondre.
.
Pour résoudre les inégalités avec tangente et cotangente, le concept de ligne de tangentes et de cotangentes est utile. Ce sont les droites et, respectivement (sur les figures (1) et (2)), les tangentes au cercle trigonométrique.
Il est facile de voir que si l'on construit un rayon dont l'origine est à l'origine des coordonnées, faisant un angle avec la direction positive de l'axe des abscisses, alors la longueur du segment du point au point d'intersection de ce rayon avec la tangente est exactement égale à la tangente de l'angle que fait ce rayon avec l'axe des abscisses. Une observation similaire se produit pour la cotangente.
Exemple Résolvez l’inégalité.
Solution. Notons , alors l'inégalité prendra la forme la plus simple : . Considérons un intervalle de longueur égale à la plus petite période positive (LPP) de la tangente. Sur ce segment, à l'aide de la ligne des tangentes, on établit que . Rappelons maintenant ce qu'il faut ajouter depuis que la centrale nucléaire fonctionne. Donc, 
. En revenant à la variable, nous obtenons cela.
Répondre.
.
Il est pratique de résoudre les inégalités avec des fonctions trigonométriques inverses à l'aide de graphiques de fonctions trigonométriques inverses. Montrons comment cela se fait avec un exemple.
Résoudre graphiquement les inégalités trigonométriques
Notez que si --- périodique fonction, alors pour résoudre l'inégalité il faut trouver sa solution sur un segment dont la longueur est égale à la période de la fonction. Toutes les solutions à l'inégalité d'origine seront constituées des valeurs trouvées, ainsi que de toutes celles qui diffèrent de celles trouvées par un nombre entier de périodes de la fonction.
Considérons la solution à l'inégalité ().
Depuis , alors l’inégalité n’a pas de solution. Si , alors l’ensemble des solutions à l’inégalité --- un tas de tous des nombres réels.
Laisser . La fonction sinusoïdale a la plus petite période positive, donc l'inégalité peut être résolue d'abord sur un segment de longueur, par exemple sur un segment. Nous construisons des graphiques de fonctions et (). sont données par des inégalités de la forme : et, d'où,
Dans ce travail, des méthodes de résolution d'équations et d'inégalités trigonométriques, à la fois simples et au niveau Olympiade, ont été envisagées. Les principales méthodes de résolution des équations trigonométriques et des inégalités ont été considérées et, de plus, comme spécifiques --- caractéristique uniquement pour les équations et inégalités trigonométriques, et les méthodes fonctionnelles générales pour résoudre les équations et les inégalités appliquées aux équations trigonométriques.
La thèse fournit des informations théoriques de base : définition et propriétés des fonctions trigonométriques et trigonométriques inverses ; exprimer des fonctions trigonométriques en termes d'autres fonctions trigonométriques, ce qui est très important pour transformer des expressions trigonométriques, notamment celles contenant des fonctions trigonométriques inverses ; En plus des formules trigonométriques de base, bien connues du cours scolaire, sont données des formules qui simplifient les expressions contenant des fonctions trigonométriques inverses. La solution des équations trigonométriques élémentaires, la méthode de factorisation et les méthodes de réduction des équations trigonométriques aux équations algébriques sont considérées. En raison du fait que les solutions des équations trigonométriques peuvent être écrites de plusieurs manières et que la forme de ces solutions ne permet pas de déterminer immédiatement si ces solutions sont identiques ou différentes, un schéma général de résolution des équations trigonométriques est considéré et la transformation de groupes de solutions générales d'équations trigonométriques est examiné en détail. Les méthodes de résolution des inégalités trigonométriques élémentaires, tant sur le cercle unité que par la méthode graphique, sont discutées en détail. Le processus de résolution des inégalités trigonométriques non élémentaires par les inégalités élémentaires et la méthode des intervalles, déjà bien connue des écoliers, est décrit. Des solutions aux tâches typiques de sélection des racines sont données. Les informations théoriques nécessaires à la sélection des racines sont données : partitionnement d'un ensemble d'entiers en sous-ensembles disjoints, résolution d'équations en entiers (diaphantine).
Les résultats de cette thèse peuvent être utilisés comme matériel pédagogique dans la préparation de cours et thèses, lors de la préparation des cours au choix pour les écoliers, le travail peut également être utilisé pour préparer les étudiants aux examens d'entrée et aux tests centralisés.
Vygodsky Ya.Ya., Manuel de mathématiques élémentaires. /Vygodsky Ya.Ya. --- M. : Nauka, 1970.
Igudisman O., Mathématiques à l'oral / Igudisman O. --- M. : Iris Press, Rolf, 2001.
Azarov A.I., équations/Azarov A.I., Gladun O.M., Fedosenko V.S. --- Mn. : Trivium, 1994.
Litvinenko V.N., Atelier sur les mathématiques élémentaires / Litvinenko V.N. --- M. : Éducation, 1991.
Sharygin I.F., Cours optionnel de mathématiques : résolution de problèmes / Sharygin I.F., Golubev V.I. --- M. : Éducation, 1991.
Bardushkin V., Équations trigonométriques. Sélection des racines/B. Bardushkin, A. Prokofiev.// Mathématiques, n° 12, 2005 p. 23-27.
Vasilevsky A.B., Devoirs pour des travaux parascolaires en mathématiques/Vasilevsky A.B. --- Mn. : Asveta du peuple. 1988. --- 176 p.
Sapunov P. I., Transformation et union de groupes de solutions générales d'équations trigonométriques / Sapunov P. I. // Enseignement mathématique, numéro 3, 1935.
Borodine P., Trigonométrie. Matériel des examens d'entrée à l'Université d'État de Moscou [texte]/P. Borodine, V. Galkin, V. Panferov, I. Sergeev, V. Tarasov // Mathématiques n° 1, 2005 p. 36-48.
Samusenko A.V., Mathématiques : Erreurs typiques des candidats : Manuel de référence / Samusenko A.V., Kazachenok V.V. --- Mn. : École supérieure, 1991.
Azarov A.I., Méthodes fonctionnelles et graphiques pour résoudre les problèmes d'examen / Azarov A.I., Barvenov S.A., --- Mn. : Aversev, 2004.
MÉTHODES DE RÉSOLUTION DES INÉGALITÉS TRIGONOMÉTRIQUES
Pertinence. Historiquement, les équations trigonométriques et les inégalités ont occupé une place particulière dans les programmes scolaires. On peut dire que la trigonométrie est l'une des sections les plus importantes du cours scolaire et de l'ensemble science mathématique en général.
Les équations trigonométriques et les inégalités occupent l'une des places centrales du cours de mathématiques au secondaire, tant en termes de contenu du matériel pédagogique que de méthodes d'activité éducative et cognitive qui peuvent et doivent être formées au cours de leur étude et appliquées à la résolution d'un grand nombre. de problèmes d'ordre théorique et appliqué.
La résolution d’équations trigonométriques et d’inégalités crée les conditions préalables à la systématisation des connaissances des élèves dans tous les domaines Matériel pédagogique en trigonométrie (par exemple, propriétés des fonctions trigonométriques, méthodes de transformation d'expressions trigonométriques, etc.) et permet d'établir des connexions efficaces avec la matière étudiée en algèbre (équations, équivalence d'équations, inégalités, transformations identitaires expressions algébriques, etc.).
En d'autres termes, la réflexion sur les techniques de résolution d'équations trigonométriques et d'inégalités implique une sorte de transfert de ces compétences vers de nouveaux contenus.
L'importance de la théorie et ses nombreuses applications témoignent de la pertinence du sujet choisi. Cela vous permet à son tour de déterminer les buts, les objectifs et le sujet de recherche du travail de cours.
But de l'étude: généraliser les types d'inégalités trigonométriques disponibles, les méthodes de base et spéciales pour les résoudre, sélectionner un ensemble de problèmes pour résoudre les inégalités trigonométriques par les écoliers.
Objectifs de recherche:
1. Sur la base d'une analyse de la littérature disponible sur le sujet de recherche, systématiser le matériel.
2. Fournir un ensemble de tâches nécessaires à la consolidation du thème « Inégalités trigonométriques ».
Objet d'étude sont des inégalités trigonométriques dans le cours de mathématiques à l'école.
Sujet d'étude: types d'inégalités trigonométriques et méthodes pour les résoudre.
Signification théorique est de systématiser le matériel.
Importance pratique: application des connaissances théoriques à la résolution de problèmes ; analyse des principales méthodes courantes de résolution des inégalités trigonométriques.
Méthodes de recherche : analyse de la littérature scientifique, synthèse et généralisation des connaissances acquises, analyse de résolution de problèmes, recherche de méthodes optimales de résolution des inégalités.
§1. Types d'inégalités trigonométriques et méthodes de base pour les résoudre
1.1. Les inégalités trigonométriques les plus simples
Deux expressions trigonométriques, reliées par le signe ou >, sont appelées inégalités trigonométriques.
Résoudre une inégalité trigonométrique signifie trouver l'ensemble des valeurs des inconnues incluses dans l'inégalité pour lesquelles l'inégalité est satisfaite.
L'essentiel des inégalités trigonométriques est résolu en les réduisant à la solution la plus simple :
Il peut s'agir d'une méthode de factorisation, de changement de variable ( 
, 
etc.), où l'inégalité habituelle est d'abord résolue, puis une inégalité de la forme 
etc., ou d'autres méthodes.
Les inégalités les plus simples peuvent être résolues de deux manières : en utilisant le cercle unité ou graphiquement.
Laisserf(x
– une des fonctions trigonométriques de base. Pour résoudre l'inégalité 
il suffit de trouver sa solution sur une période, c'est-à-dire sur tout segment dont la longueur est égale à la période de la fonctionF
X
. Alors la solution à l’inégalité initiale sera entièrement trouvéeX
, ainsi que les valeurs qui diffèrent de celles trouvées par n'importe quel nombre entier de périodes de la fonction. Dans ce cas, il est préférable d’utiliser la méthode graphique.
Donnons un exemple d'algorithme de résolution d'inégalités 
(
) Et 
.
Algorithme pour résoudre les inégalités (
).
1. Formuler la définition du sinus d'un nombreX sur le cercle unité.
3. Sur l'axe des ordonnées, marquez le point avec la coordonnéeun .
4. Tracez une ligne parallèle à l'axe OX passant par ce point et marquez ses points d'intersection avec le cercle.
5. Sélectionnez un arc de cercle dont tous les points ont une ordonnée inférieure àun .
6. Indiquez le sens du tour (dans le sens inverse des aiguilles d'une montre) et notez la réponse en ajoutant le point de la fonction aux extrémités de l'intervalle2πn
,
.
Algorithme pour résoudre les inégalités .
1. Formuler la définition de la tangente d'un nombreX sur le cercle unité.
2. Dessinez un cercle unité.
3. Tracez une ligne de tangentes et marquez un point avec une ordonnée dessusun .
4. Reliez ce point à l'origine et marquez le point d'intersection du segment résultant avec le cercle unité.
5. Sélectionnez un arc de cercle dont tous les points ont une ordonnée sur la ligne tangente inférieure àun .
6. Indiquez le sens du parcours et écrivez la réponse en tenant compte du domaine de définition de la fonction, en ajoutant un pointπn
,
(le chiffre à gauche de l'entrée est toujours inférieur au chiffre à droite).
L'interprétation graphique des solutions aux équations et formules les plus simples pour résoudre les inégalités sous forme générale est indiquée en annexe (Annexes 1 et 2).
Exemple 1.
Résoudre l'inégalité 
.
Tracez une ligne droite sur le cercle unité 
, qui coupe le cercle aux points A et B.
Toutes les significationsoui
sur l'intervalle NM est plus grand
, tous les points de l'arc AMB satisfont à cette inégalité. À tous les angles de rotation, grand 
, mais plus petit 
,
prendra des valeurs plus grandes
(mais pas plus d'un).
Fig. 1
Ainsi, la solution de l'inégalité sera toutes les valeurs de l'intervalle 
, c'est à dire. 
. Pour obtenir toutes les solutions de cette inégalité, il suffit d'ajouter aux extrémités de cet intervalle 
, Où 
, c'est à dire. 
,
.
Notez que les valeurs 
Et 
sont les racines de l'équation 
,
ceux. 
;
.
Répondre: 
, .
1.2. Méthode graphique
En pratique, la méthode graphique de résolution des inégalités trigonométriques s'avère souvent utile. Considérons l'essence de la méthode en utilisant l'exemple de l'inégalité 
:
1. Si l’argument est complexe (différent deX ), puis remplacez-le part .
2. Nous construisons en un avion coordonné
jouet
graphiques de fonctions 
Et 
.
3. Nous trouvons teldeux points adjacents d'intersection de graphiques, entre lesquelsonde sinusoïdalesituéplus haut
droit . On retrouve les abscisses de ces points.
4. Écrivez une double inégalité pour l'argumentt , en tenant compte de la période cosinus (t sera entre les abscisses trouvées).
5. Effectuez une substitution inverse (retour à l'argument d'origine) et exprimez la valeurX à partir de la double inégalité, on écrit la réponse sous la forme d'un intervalle numérique.
Exemple 2. Résoudre l'inégalité : .
Lors de la résolution d'inéquations à l'aide de la méthode graphique, il est nécessaire de construire des graphiques de fonctions aussi précisément que possible. Transformons l'inégalité sous la forme :
Construisons des graphiques de fonctions dans un système de coordonnées 
Et 
(Fig.2).
Figure 2
Les graphiques des fonctions se croisent au pointUN
avec coordonnées 
; 
. Entre 
points du graphique 
sous les points du graphique 
. Et quand les valeurs de la fonction sont les mêmes. C'est pourquoi à 
.
Répondre: 
.
1.3. Méthode algébrique
Très souvent, l'inégalité trigonométrique originale peut être réduite à une inégalité algébrique (rationnelle ou irrationnelle) grâce à une substitution bien choisie. Cette méthode consiste à transformer une inégalité, à introduire une substitution ou à remplacer une variable.
Examinons des exemples spécifiques d'application de cette méthode.
Exemple 3.
Réduction à la forme la plus simple 
.
(Fig.3)
Figure 3
, 
.
Répondre: 
,
Exemple 4. Résoudre les inégalités :
ODZ : 
, 
.
Utiliser des formules : 
, 
Écrivons l'inégalité sous la forme : 
.
Ou, croyant 
après de simples transformations on obtient
,
,
.
En résolvant la dernière inéquation par la méthode des intervalles, on obtient :
Figure 4
, respectivement 
. Puis à partir de la Fig. 4 suit 
, Où 
.
Figure 5
Répondre: 
, 
.
1.4. Méthode d'intervalle
Régime général résoudre des inégalités trigonométriques à l'aide de la méthode des intervalles :
Factoriser à l'aide de formules trigonométriques.
Trouvez les points de discontinuité et les zéros de la fonction et placez-les sur le cercle.
Prenez n'importe quel pointÀ (mais introuvable plus tôt) et découvrez le signe du produit. Si le produit est positif, alors placez un point en dehors du cercle unité sur le rayon correspondant à l'angle. Sinon, placez le point à l'intérieur du cercle.
Si un point apparaît un nombre pair de fois, nous l’appelons un point de multiplicité paire ; s’il se produit un nombre impair de fois, nous l’appelons un point de multiplicité impaire. Dessinez des arcs comme suit : commencez à partir d'un pointÀ , si le point suivant est de multiplicité impaire, alors l'arc coupe le cercle en ce point, mais si le point est de multiplicité paire, alors il ne coupe pas.
Les arcs derrière le cercle sont des intervalles positifs ; à l’intérieur du cercle il y a des espaces négatifs.
Exemple 5. Résoudre les inégalités
, 
.
Points de la première série : 
.
Points de la deuxième série : 
.
Chaque point apparaît un nombre impair de fois, c’est-à-dire que tous les points sont de multiplicité impaire.
Découvrons le signe du produit sur 
: . Marquons tous les points sur le cercle unité (Fig. 6) :
Riz. 6
Répondre: 
, 
; 
, 
; 
, 
.
Exemple 6 . Résoudre l'inégalité.
Solution:
Trouvons les zéros de l'expression .
Recevoiraem :
,
;
, 
;
, 
;
, 
;
Sur les valeurs de la série du cercle unitaireX
1
représenté par des points 
. SérieX
2
donne des points 
. Une sérieX
3
nous obtenons deux points 
. Enfin, la sérieX
4
représentera des points 
. Traçons tous ces points sur le cercle unité, en indiquant sa multiplicité entre parenthèses à côté de chacun d'eux.
Laissez maintenant le numéro 
sera égal. Faisons une estimation en fonction du signe :
Alors, point finalUN
doit être sélectionné sur le rayon formant l'angle 
avec poutreOh,
en dehors du cercle unité. (Notez que le faisceau auxiliaireÀ PROPOS
UN
Il n’est pas du tout nécessaire de le représenter en image. PointUN
est choisi approximativement.)
Maintenant du point de vueUN
tracez une ligne continue ondulée séquentiellement vers tous les points marqués. Et à des points notre ligne va d'une zone à une autre : si elle était à l'extérieur du cercle unité, alors elle passe à l'intérieur de celui-ci. On approche du point 
, la droite revient à la région intérieure, puisque la multiplicité de ce point est paire. De même au point 
(avec une multiplicité égale), la ligne doit être tournée vers la région extérieure. Nous avons donc dessiné une certaine image présentée sur la Fig. 7. Cela aide à mettre en évidence les zones souhaitées sur le cercle unitaire. Ils sont marqués du signe « + ».
Figure 7
Réponse finale:
Note. Si une ligne ondulée, après avoir contourné tous les points marqués sur le cercle unité, ne peut être ramenée au pointUN , sans traverser le cercle à un endroit « illégal », cela signifie qu'une erreur a été commise dans la solution, à savoir qu'un nombre impair de racines a été manqué.
Répondre: .
§2. Un ensemble de problèmes pour résoudre les inégalités trigonométriques
Dans le processus de développement de la capacité des écoliers à résoudre les inégalités trigonométriques, 3 étapes peuvent également être distinguées.
1. préparatoire,
2. développer la capacité de résoudre des inégalités trigonométriques simples ;
3. introduction d'inégalités trigonométriques d'autres types.
Le but de l'étape préparatoire est qu'il est nécessaire de développer chez les écoliers la capacité d'utiliser un cercle ou un graphique trigonométrique pour résoudre des inégalités, à savoir :
Capacité à résoudre des inégalités simples de la forme ,
, ,
,
utiliser les propriétés des fonctions sinus et cosinus ;
Capacité à construire des inégalités doubles pour des arcs de cercle numérique ou pour des arcs de graphiques de fonctions ;
Capacité à effectuer diverses transformations d'expressions trigonométriques.
Il est recommandé de mettre en œuvre cette étape dans le processus de systématisation des connaissances des écoliers sur les propriétés des fonctions trigonométriques. Les principaux moyens peuvent être des tâches proposées aux étudiants et réalisées soit sous la direction d'un enseignant, soit de manière indépendante, ainsi que des compétences développées dans la résolution d'équations trigonométriques.
Voici des exemples de telles tâches :
1
. Marquez un point sur le cercle unité 
, Si
.
2.
Dans quel quart du plan de coordonnées se trouve le point ? , Si 
équivaut à: 
3.
Marquez les points sur le cercle trigonométrique , Si:
4. Convertir l'expression en fonctions trigonométriquesjequarts.
UN) 
,
b) 
,
V) 
5. Arc MR est donné.M - milieuje-ème quart-temps,R. - milieuIIème trimestre. Limiter la valeur d'une variablet pour : (faire une double inégalité) a) arc MR ; b) Arcs RM.
6. Notez la double inégalité pour les sections sélectionnées du graphique :
Riz. 1
7.
Résoudre les inégalités 
, 
, 
, 
.
8. Convertir l'expression .
Lors de la deuxième étape de l'apprentissage de la résolution des inégalités trigonométriques, nous pouvons proposer les recommandations suivantes liées à la méthodologie d'organisation des activités étudiantes. Dans ce cas, il est nécessaire de se concentrer sur les compétences existantes des étudiants dans le travail avec un cercle ou un graphique trigonométrique, formé lors de la résolution des équations trigonométriques les plus simples.
Premièrement, on peut motiver l'opportunité d'obtenir une méthode générale de résolution des inégalités trigonométriques les plus simples en se tournant, par exemple, vers une inégalité de la forme 
.
Utiliser les connaissances et les compétences acquises à étape préparatoire, les élèves réduiront l’inégalité proposée sous la forme 
, mais peut avoir du mal à trouver un ensemble de solutions à l’inégalité qui en résulte, car Il est impossible de le résoudre uniquement en utilisant les propriétés de la fonction sinus. Cette difficulté peut être évitée en se tournant vers l'illustration appropriée (en résolvant l'équation graphiquement ou en utilisant un cercle unité).
Deuxièmement, l’enseignant doit attirer l’attention des élèves sur les différentes manières d’accomplir la tâche, donner un exemple approprié de résolution de l’inégalité à la fois graphiquement et à l’aide d’un cercle trigonométrique.
Considérons les solutions suivantes à l'inégalité .
1. Résoudre l’inégalité à l’aide du cercle unité.
Dans la première leçon sur la résolution des inégalités trigonométriques, nous proposerons aux étudiants un algorithme de solution détaillé qui, dans une présentation étape par étape, reflète toutes les compétences de base nécessaires pour résoudre l'inégalité.
Étape 1.Traçons un cercle unité et marquons un point sur l'axe des ordonnées 
et tracez une ligne droite qui le traverse parallèlement à l’axe des x. Cette ligne coupera le cercle unité en deux points. Chacun de ces points représente des nombres dont le sinus est égal à .
Étape 2.Cette ligne droite divisait le cercle en deux arcs. Sélectionnons celui qui représente les nombres dont le sinus est supérieur à . Naturellement, cet arc se situe au dessus de la ligne droite tracée.
Riz. 2
Étape 3.Sélectionnez l'une des extrémités de l'arc marqué. Écrivons l'un des nombres représentés par ce point du cercle unité 
.
Étape 4.Afin de sélectionner le numéro correspondant à la deuxième extrémité de l'arc sélectionné, on « marche » le long de cet arc de l'extrémité nommée à l'autre. Dans le même temps, rappelez-vous qu'en vous déplaçant dans le sens inverse des aiguilles d'une montre, les nombres que nous traverserons augmenteront (en vous déplaçant dans la direction opposée, les nombres diminueront). Écrivons le nombre représenté sur le cercle unité à la deuxième extrémité de l'arc marqué 
.
On voit donc que l'inégalité satisfaire les nombres pour lesquels l'inégalité est vraie 
. Nous avons résolu l'inégalité pour les nombres situés sur la même période de la fonction sinus. Par conséquent, toutes les solutions à l’inégalité peuvent s’écrire sous la forme 
Il convient de demander aux élèves d'examiner attentivement le dessin et de comprendre pourquoi toutes les solutions à l'inégalité peut s'écrire sous la forme 
, 
.
Riz. 3
Il est nécessaire d'attirer l'attention des élèves sur le fait que lors de la résolution des inégalités pour la fonction cosinus, on trace une droite parallèle à l'axe des ordonnées.
Méthode graphique pour résoudre les inégalités.
Nous construisons des graphiques 
Et 
, étant donné que 
.
Riz. 4
Ensuite, nous écrivons l'équation 
et sa décision 
, 
, 
, trouvé à l'aide de formules 
, 
, 
.
(Donnantn
valeurs 0, 1, 2, on retrouve les trois racines de l'équation compilée). Valeurs 
sont trois abscisses consécutives des points d'intersection des graphiques Et . Évidemment, toujours à l'intervalle 
l’inégalité persiste 
, et sur l'intervalle 
- inégalité 
. On s'intéresse au premier cas, puis en ajoutant aux extrémités de cet intervalle un nombre multiple de la période du sinus, on obtient une solution de l'inégalité comme: 
, .
Riz. 5
Résumer. Pour résoudre l'inégalité , vous devez créer l’équation correspondante et la résoudre. Trouvez les racines de la formule résultante 
Et 
, et écrivez la réponse à l’inégalité sous la forme : , .
Troisièmement, le fait concernant l'ensemble des racines de l'inégalité trigonométrique correspondante est très clairement confirmé lors de sa résolution graphique.
Riz. 6
Il est nécessaire de démontrer aux élèves que le tour, qui est la solution de l'inégalité, se répète sur le même intervalle, égal à la période de la fonction trigonométrique. Vous pouvez également envisager une illustration similaire pour le graphique de la fonction sinus.
Quatrièmement, il convient de réaliser un travail de mise à jour des techniques des étudiants pour convertir la somme (différence) des fonctions trigonométriques en un produit, et d'attirer l'attention des étudiants sur le rôle de ces techniques dans la résolution des inégalités trigonométriques.
Ce travail peut être organisé à travers auto-exécution aux étudiants des tâches proposées par l'enseignant, parmi lesquelles nous soulignons les suivantes :
Cinquièmement, les élèves doivent illustrer la solution de chaque inégalité trigonométrique simple à l'aide d'un graphique ou d'un cercle trigonométrique. Il faut absolument faire attention à son opportunité, notamment à l'utilisation du cercle, car lors de la résolution d'inégalités trigonométriques, l'illustration correspondante constitue un moyen très pratique d'enregistrer l'ensemble des solutions à une inégalité donnée.
Il convient d'initier les étudiants aux méthodes de résolution des inégalités trigonométriques qui ne sont pas les plus simples selon le schéma suivant : recours à une inégalité trigonométrique spécifique recours à l'équation trigonométrique correspondante recherche conjointe (enseignant - élèves) d'une solution ; transfert indépendant de la méthode trouvée à d’autres inégalités du même type.
Afin de systématiser les connaissances des étudiants en trigonométrie, nous recommandons de sélectionner spécialement les inégalités dont la solution nécessite diverses transformations qui peuvent être mises en œuvre au cours du processus de résolution, et de concentrer l'attention des étudiants sur leurs caractéristiques.
Comme telles inégalités productives, nous pouvons proposer, par exemple, ce qui suit :
En conclusion, nous donnons un exemple d'un ensemble de problèmes pour résoudre des inégalités trigonométriques.
1. Résoudre les inégalités :
2. Résoudre les inégalités : 3. Trouver toutes les solutions aux inégalités : 4. Trouver toutes les solutions aux inégalités :UN) 
, satisfaisant la condition 
;
b) 
, satisfaisant la condition 
.
5. Trouver toutes les solutions aux inégalités :
UN) ;
b) ;
V) 
;
G) 
;
d) 
.
6. Résoudre les inégalités :
UN) ;
b) ;
V) ;
G) 
;
d) ;
e) ;
et) 
.
7. Résoudre les inégalités :
UN) 
;
b) ;
V) ;
G) .
8. Résoudre les inégalités :
UN) ;
b) ;
V) ;
G) 
;
d) 
;
e) ;
et) 
;
h) .
Il est conseillé de proposer les tâches 6 et 7 aux élèves étudiant les mathématiques à niveau élevé, tâche 8 – pour les étudiants des classes ayant des études avancées en mathématiques.
§3. Méthodes spéciales pour résoudre les inégalités trigonométriques
Méthodes spéciales pour résoudre des équations trigonométriques - c'est-à-dire les méthodes qui ne peuvent être utilisées que pour résoudre des équations trigonométriques. Ces méthodes sont basées sur l'utilisation des propriétés des fonctions trigonométriques, ainsi que sur l'utilisation de diverses formules et identités trigonométriques.
3.1. Méthode sectorielle
Considérons la méthode sectorielle pour résoudre les inégalités trigonométriques. Résoudre les inégalités de la forme 
, OùP.
(
X
)
EtQ
(
X
)
– les fonctions trigonométriques rationnelles (les sinus, les cosinus, les tangentes et les cotangentes y sont incluses rationnellement), similaires à la résolution d'inégalités rationnelles. Il est pratique de résoudre les inégalités rationnelles en utilisant la méthode des intervalles sur la droite numérique. Son analogue pour résoudre les inégalités trigonométriques rationnelles est la méthode des secteurs dans le cercle trigonométrique, par exemplepéché
Etcosx
(
) ou demi-cercle trigonométrique pourtgx
Etctgx
(
).
Dans la méthode des intervalles, chaque facteur linéaire du numérateur et du dénominateur de la forme 
sur l'axe des nombres correspond à un point 
, et en passant par ce point change de signe. Dans la méthode sectorielle, chaque facteur de la forme 
, Où 
- une des fonctionspéché
oucosx
Et 
, dans un cercle trigonométrique correspondent deux angles 
Et 
, qui divise le cercle en deux secteurs. En passant par Et fonction change de signe.
Il faut retenir les éléments suivants :
a) Facteurs de forme 
Et 
, Où 
, conserve le signe pour toutes les valeurs 
. Ces facteurs du numérateur et du dénominateur sont écartés en changeant (si 
) à chacun de ces rejets, le signe de l'inégalité est inversé.
b) Facteurs de forme 
Et 
sont également rejetés. De plus, s'il s'agit de facteurs du dénominateur, alors des inégalités de forme s'ajoutent au système d'inégalités équivalent 
Et 
. Si ce sont des facteurs du numérateur, alors dans le système équivalent de restrictions ils correspondent aux inégalités Et dans le cas d'une inégalité initiale stricte, et l'égalité 
Et 
dans le cas d’une inégalité initiale non stricte. Lors de la suppression du multiplicateur 
ou 
le signe de l'inégalité est inversé.
Exemple 1.
Résoudre les inégalités : a) 
, b) 
.
nous avons la fonction b) . Résoudre l'inégalité que nous avons,
3.2. Méthode du cercle concentrique
Cette méthode est un analogue de la méthode des axes de nombres parallèles pour résoudre des systèmes d'inégalités rationnelles.
Prenons un exemple de système d'inégalités.
Exemple 5.
Résoudre un système d'inégalités trigonométriques simples 
Tout d’abord, nous résolvons chaque inégalité séparément (Figure 5). Dans le coin supérieur droit de la figure, nous indiquerons pour quel argument le cercle trigonométrique est considéré.
Figure 5
Ensuite, nous construisons un système de cercles concentriques pour l’argumentX . Nous dessinons un cercle et l'ombrons selon la solution de la première inégalité, puis nous dessinons un cercle d'un plus grand rayon et l'ombrons selon la solution de la seconde, puis nous construisons un cercle pour la troisième inégalité et un cercle de base. Nous dessinons des rayons depuis le centre du système jusqu'aux extrémités des arcs afin qu'ils coupent tous les cercles. Nous formons une solution sur le cercle de base (Figure 6).
Figure 6
Répondre:
, 
.
Conclusion
Tous les objectifs de la recherche du cours ont été atteints. Le matériel théorique est systématisé : les principaux types d'inégalités trigonométriques et les principales méthodes pour les résoudre sont données (graphique, algébrique, méthode des intervalles, secteurs et méthode des cercles concentriques). Un exemple de résolution d’inégalité a été donné pour chaque méthode. La partie théorique a été suivie par la partie pratique. Il contient un ensemble de tâches pour résoudre les inégalités trigonométriques.
Ce cours peut être utilisé par les étudiants pour travail indépendant. Les écoliers peuvent vérifier le niveau de maîtrise de ce sujet et s'entraîner à accomplir des tâches de complexité variable.
Après avoir étudié la littérature pertinente sur cette question, nous pouvons évidemment conclure que la capacité et les compétences nécessaires pour résoudre les inégalités trigonométriques dans le cours scolaire d'algèbre et d'analyse élémentaire sont très importantes, dont le développement nécessite des efforts importants de la part du professeur de mathématiques.
C'est pourquoi ce travail sera utile aux professeurs de mathématiques, car il permet d'organiser efficacement la formation des étudiants sur le thème « Inégalités trigonométriques ».
La recherche peut être poursuivie en l'élargissant jusqu'à un ouvrage final qualifiant.
Liste de la littérature utilisée
Bogomolov, N.V. Recueil de problèmes en mathématiques [Texte] / N.V. Bogomolov. – M. : Outarde, 2009. – 206 p.
Vygodsky, M. Ya. Manuel de mathématiques élémentaires [Texte] / M.Ya. Vygodski. – M. : Outarde, 2006. – 509 p.
Jourbenko, L.N. Mathématiques en exemples et problèmes [Texte] / L.N. Jourbenko. – M. : Infra-M, 2009. – 373 p.
Ivanov, O.A. Mathématiques élémentaires pour écoliers, étudiants et enseignants [Texte] / O.A. Ivanov. – M. : MTsNMO, 2009. – 384 p.
Karp, A.P. Travaux d'algèbre et débuts de l'analyse pour l'organisation du redoublement final et de la certification en 11e année [Texte] / A.P. Carpe. – M. : Éducation, 2005. – 79 p.
Koulanine, E.D. 3000 problèmes de concours en mathématiques [Texte] / E.D. Koulanine. – M. : Iris-presse, 2007. – 624 p.
Leibson, K.L. Collection tâches pratiques en mathématiques [Texte] / K.L. Leibson. – M. : Outarde, 2010. – 182 p.
Coude, V.V. Problèmes avec les paramètres et leurs solutions. Trigonométrie : équations, inégalités, systèmes. 10e année [Texte] / V.V. Coude. – M. : ARKTI, 2008. – 64 p.
Manova, A.N. Mathématiques. Tuteur express pour la préparation à l'examen d'État unifié : étudiant. manuel [Texte] / A.N. Manova. – Rostov-sur-le-Don : Phoenix, 2012. – 541 p.
Mordkovitch, A.G. Algèbre et début de l'analyse mathématique. 10-11 années. Manuel pour les étudiants les établissements d'enseignement[Texte] / A.G. Mordkovitch. – M. : Iris-presse, 2009. – 201 p.
Novikov, A.I. Fonctions trigonométriques, équations et inégalités [Texte] / A.I. Novikov. – M. : FIZMATLIT, 2010. – 260 p.
Oganesyan, V.A. Méthodes d'enseignement des mathématiques en lycée: Technique générale. Cahier de texte manuel pour les étudiants en physique - tapis. faux. péd. Inst. [Texte] / V.A. Oganesian. – M. : Éducation, 2006. – 368 p.
Olehnik, S.N. Équations et inégalités. Méthodes de solution non standard [Texte] / S.N. Olehnik. – M. : Maison d'édition Factorial, 1997. – 219 p.
Sevryukov, P.F. Trigonométrique, exponentielle et équations logarithmiques et inégalités [Texte] / P.F. Sevryukov. – M. : Instruction publique, 2008. – 352 p.
Sergueïev, I.N. Examen d'État unifié : 1000 problèmes avec réponses et solutions en mathématiques. Toutes les tâches du groupe C [Texte] / I.N. Sergueïev. – M. : Examen, 2012. – 301 p.
Sobolev, A.B. Mathématiques élémentaires [Texte] / A.B. Sobolev. – Ekaterinbourg : Établissement d'enseignement public d'enseignement professionnel supérieur USTU-UPI, 2005. – 81 p.
Fenko, L.M. Méthode des intervalles dans la résolution des inégalités et l'étude des fonctions [Texte] / L.M. Fenko. – M. : Outarde, 2005. – 124 p.
Friedman, L.M. Base théorique méthodes d'enseignement des mathématiques [Texte] / L.M. Friedmann. – M. : Maison du livre « LIBROKOM », 2009. – 248 p.
Annexe 1
Interprétation graphique de solutions à des inégalités simples
Riz. 1
Riz. 2
Figure 3
Figure 4
Figure 5
Figure 6
Figure 7
Figure 8
Annexe 2
Solutions aux inégalités simples
Projet d'algèbre « Résoudre les inégalités trigonométriques » Réalisé par l'élève de la classe 10 « B » Kazachkova Yulia Superviseur : professeur de mathématiques Kochakova N.N.
Objectif Consolider le matériel sur le thème «Résoudre les inégalités trigonométriques» et créer un rappel pour que les étudiants se préparent à l'examen à venir.
Objectifs : Résumer le matériel sur ce sujet. Systématiser les informations reçues. Considérez ce sujet dans l'examen d'État unifié.
Pertinence La pertinence du sujet que j'ai choisi réside dans le fait que des tâches sur le thème « Résoudre les inégalités trigonométriques » sont incluses dans les tâches de l'examen d'État unifié.
Inégalités trigonométriques Une inégalité est une relation reliant deux nombres ou expressions par l'un des signes : (supérieur à) ; ≥ (supérieur ou égal à). Une inégalité trigonométrique est une inégalité impliquant des fonctions trigonométriques.
Inégalités trigonométriques La solution des inégalités contenant des fonctions trigonométriques se réduit, en règle générale, à la solution des inégalités les plus simples de la forme : sin x>a, sin x une, parce que x un, tg x a, ctg x
Algorithme de résolution des inégalités trigonométriques Sur l'axe correspondant à une fonction trigonométrique donnée, marquez ceci valeur numérique cette fonction. Tracez une ligne passant par le point marqué coupant le cercle unité. Sélectionnez les points d'intersection d'une droite et d'un cercle en tenant compte du signe d'inégalité stricte ou non stricte. Sélectionnez l'arc de cercle sur lequel se situent les solutions de l'inégalité. Déterminez les valeurs d'angle aux points de départ et d'arrivée de l'arc de cercle. Écrivez la solution de l'inégalité en tenant compte de la périodicité de la fonction trigonométrique donnée.
Formules pour résoudre les inégalités trigonométriques sinx >a ; x (arcsin a + 2πn ; π- arcsin a + 2πn). péché un; x (- arccos a + 2πn ; arccos a + 2πn). cosxun; x (arctg a + πn ; + πn). tgx un; x (πn ; arctan + πn). ctgx
Solution graphique des inégalités trigonométriques de base sinx >a
Solution graphique des inégalités trigonométriques de base sinx Solution graphique des inégalités trigonométriques de base cosx >a Solution graphique des inégalités trigonométriques de base cosx Solution graphique des inégalités trigonométriques de base tgx >a Solution graphique des inégalités trigonométriques de base tgx Solution graphique des inégalités trigonométriques de base ctgx >a
Sur leçon pratique Nous répéterons les principaux types de tâches du thème « Trigonométrie », analyserons en outre des problèmes de complexité accrue et examinerons des exemples de résolution de diverses inégalités trigonométriques et de leurs systèmes.
Cette leçon vous aidera à vous préparer à l'un des types de tâches B5, B7, C1 et C3.
Commençons par passer en revue les principaux types de tâches que nous avons abordées dans le sujet « Trigonométrie » et résolvons plusieurs problèmes non standard.
Tâche n°1. Convertir les angles en radians et degrés : a) ; b) .
a) Utilisons la formule pour convertir les degrés en radians
Remplaçons-y la valeur spécifiée.
b) Appliquer la formule de conversion des radians en degrés
Effectuons la substitution 
.
Répondre. UN) ; b) .
Tâche n°2. Calculer : a) ; b) .
a) Puisque l'angle dépasse largement le tableau, nous allons le réduire en soustrayant la période sinusoïdale. Parce que L'angle est indiqué en radians, on considérera alors la période comme .
b) Dans ce cas, la situation est similaire. Puisque l’angle est indiqué en degrés, nous considérerons la période de la tangente comme .
L'angle résultant, bien que plus petit que la période, est plus grand, ce qui signifie qu'il ne se réfère plus à la partie principale, mais à la partie étendue du tableau. Afin de ne pas entraîner une nouvelle fois votre mémoire en mémorisant le tableau étendu des valeurs trigofonctionnelles, soustrayons à nouveau la période tangente :
Nous avons profité de la bizarrerie de la fonction tangente.
Répondre. une) 1 ; b) .
Tâche n°3. Calculer 
, Si .
Réduisons l'expression entière aux tangentes en divisant le numérateur et le dénominateur de la fraction par . En même temps, nous ne pouvons pas avoir peur, car dans ce cas, la valeur tangente n’existerait pas.
Tâche n°4. Simplifiez l'expression.
Les expressions spécifiées sont converties à l'aide de formules de réduction. Ils sont tout simplement inhabituellement écrits en utilisant des diplômes. La première expression représente généralement un nombre. Simplifions toutes les trigofonctions une à une :
Parce que , alors la fonction se transforme en cofonction, c'est-à-dire à la cotangente, et l'angle tombe dans le deuxième quart, dans lequel la tangente d'origine a un signe négatif.
Pour les mêmes raisons que dans l’expression précédente, la fonction se transforme en cofonction, c’est-à-dire à la cotangente, et l'angle tombe dans le premier quart, dans lequel la tangente d'origine a un signe positif.
Remplaçons le tout par une expression simplifiée :
Problème n°5. Simplifiez l'expression.
Écrivons la tangente du double angle en utilisant la formule appropriée et simplifions l'expression :
La dernière identité est l'une des formules universelles de remplacement du cosinus.
Problème n°6. Calculer.
L'essentiel est de ne pas commettre l'erreur standard et de ne pas donner la réponse selon laquelle l'expression est égale à . Vous ne pouvez pas utiliser la propriété de base de l’arctangente tant qu’il y a un facteur sous la forme de deux à côté d’elle. Pour s'en débarrasser, nous écrirons l'expression selon la formule de la tangente d'un angle double, en traitant , comme un argument ordinaire.
Nous pouvons maintenant appliquer la propriété de base de l’arctangente ; rappelez-vous qu’il n’y a aucune restriction sur son résultat numérique.
Problème n°7. Résous l'équation.
Lors de la résolution d'une équation fractionnaire égale à zéro, il est toujours indiqué que le numérateur égal à zéro, mais le dénominateur ne l'est pas, car Vous ne pouvez pas diviser par zéro.
La première équation est un cas particulier de l’équation la plus simple pouvant être résolue à l’aide d’un cercle trigonométrique. Rappelez-vous vous-même cette solution. La deuxième inégalité est résolue comme l'équation la plus simple en utilisant la formule générale des racines de la tangente, mais uniquement avec un signe différent de.
Comme nous le voyons, une famille de racines exclut une autre famille exactement du même type de racines qui ne satisfait pas à l’équation. Ceux. il n'y a pas de racines.
Répondre. Il n'y a pas de racines.
Problème n°8. Résous l'équation.
Notons tout de suite qu'on peut retirer le facteur commun et faisons-le :
L'équation a été réduite à l'une des formes standard, où le produit de plusieurs facteurs est égal à zéro. On sait déjà que dans ce cas, soit l'un d'eux est égal à zéro, soit l'autre, soit le troisième. Écrivons cela sous la forme d'un ensemble d'équations :
Les deux premières équations sont des cas particuliers des plus simples ; nous avons déjà rencontré plusieurs fois des équations similaires, nous indiquerons donc immédiatement leurs solutions. Nous réduisons la troisième équation à une fonction en utilisant la formule du sinus à double angle.
Résolvons la dernière équation séparément :
Cette équation n'a pas de racines, car la valeur sinusoïdale ne peut pas dépasser 
.
Ainsi, la solution n'est constituée que des deux premières familles de racines ; elles peuvent être combinées en une seule, ce qui est facile à montrer sur le cercle trigonométrique :
 |
Il s'agit d'une famille composée de toutes les moitiés, c'est-à-dire
Passons à la résolution des inégalités trigonométriques. Tout d'abord, nous analyserons l'approche pour résoudre l'exemple sans utiliser de formules de solutions générales, mais en utilisant le cercle trigonométrique.
Problème n°9. Résoudre les inégalités.
Traçons une ligne auxiliaire sur le cercle trigonométrique correspondant à une valeur sinusoïdale égale à , et montrons la plage d'angles qui satisfont l'inégalité.
 |
Il est très important de comprendre exactement comment indiquer l'intervalle d'angles résultant, c'est-à-dire quel est son début et quelle est sa fin. Le début de l'intervalle sera l'angle correspondant au point que l'on entrera au tout début de l'intervalle si l'on se déplace dans le sens inverse des aiguilles d'une montre. Dans notre cas, c'est le point qui se trouve à gauche, car en nous déplaçant dans le sens inverse des aiguilles d'une montre et en passant par le bon point, nous quittons au contraire la plage d'angles requise. Le bon point correspondra donc à la fin de l’écart.
Nous devons maintenant comprendre les angles du début et de la fin de notre intervalle de solutions à l’inégalité. Une erreur typique est d'indiquer immédiatement que le point droit correspond à l'angle, celui de gauche et de donner la réponse. Ce n'est pas vrai! Attention, nous venons d'indiquer l'intervalle correspondant à la partie supérieure du cercle, même si c'est la partie inférieure qui nous intéresse, autrement dit, nous avons confondu le début et la fin de l'intervalle de solution dont nous avons besoin.
Pour que l'intervalle commence au coin du point droit et se termine au coin du point gauche, il faut que le premier angle spécifié soit inférieur au second. Pour ce faire, nous devrons mesurer l'angle du point droit dans la direction de référence négative, c'est-à-dire dans le sens des aiguilles d'une montre et ce sera égal à . Ensuite, en commençant à nous déplacer dans le sens positif des aiguilles d'une montre, nous arriverons au point droit après le point gauche et obtiendrons la valeur de l'angle correspondant. Or le début de l'intervalle des angles est inférieur à la fin, et on peut écrire l'intervalle des solutions sans tenir compte de la période :
Considérant que de tels intervalles seront répétés un nombre infini de fois après tout nombre entier de rotations, on obtient une solution générale prenant en compte la période sinusoïdale :
On met des parenthèses car l'inégalité est stricte, et on repère les points sur le cercle qui correspondent aux extrémités de l'intervalle.
Comparez la réponse que vous recevez avec la formule de la solution générale que nous avons donnée dans le cours.
Répondre. 
.
Cette méthode est utile pour comprendre d'où viennent les formules de solutions générales des inégalités trigones les plus simples. De plus, il est utile pour ceux qui sont trop paresseux d’apprendre toutes ces formules encombrantes. Cependant, la méthode elle-même n'est pas non plus facile : choisissez l'approche de solution qui vous convient le mieux.
Pour résoudre les inégalités trigonométriques, vous pouvez également utiliser des graphiques de fonctions sur lesquels une ligne auxiliaire est construite, similaire à la méthode illustrée à l'aide d'un cercle unité. Si vous êtes intéressé, essayez de trouver vous-même cette approche de la solution. À l'avenir, nous utiliserons formules générales pour résoudre des inégalités trigonométriques simples.
Problème n°10. Résoudre les inégalités.
Utilisons la formule de la solution générale, en tenant compte du fait que l'inégalité n'est pas stricte :
Dans notre cas nous obtenons :
Répondre. 
Problème n°11. Résoudre les inégalités.
Utilisons la formule générale de solution pour l'inégalité strictement correspondante :
Répondre. 
.
Problème n°12. Résoudre les inégalités : a) ; b) .
Dans ces inégalités, il n'est pas nécessaire de se précipiter pour utiliser des formules de solutions générales ou du cercle trigonométrique, il suffit de mémoriser simplement la plage de valeurs du sinus et du cosinus.
a) Depuis 
, alors l’inégalité n’a pas de sens. Il n’y a donc pas de solutions.
b) Parce que de même, le sinus de tout argument satisfait toujours à l'inégalité spécifiée dans la condition. Par conséquent, toutes les valeurs réelles de l'argument satisfont à l'inégalité.
Répondre. a) il n'y a pas de solutions ; b) .
Problème 13. Résoudre les inégalités 
.
