Problem broj 1
Logika je jednostavna: ponašat ćemo se kao i prije, uprkos činjenici da sada trigonometrijske funkcije imaju složeniji argument!
Ako bismo riješili jednačinu oblika:
Zatim bismo zapisali sljedeći odgovor:
ili (od)
Ali sada u našoj ulozi imamo sljedeći izraz:
Tada možete napisati:
Naš cilj sa Vama je da lijevi štand bude jednostavan, bez ikakvih "nečistoća"!
Riješimo ih se postepeno!
Prvo uklanjamo nazivnik na: za ovo pomnožimo našu jednakost sa:
Sada ga se riješimo tako što ćemo oba dijela podijeliti na njega:
A sada da se riješimo osam:
Rezultirajući izraz se može napisati kao 2 serije rješenja (po analogiji s kvadratnom jednadžbom, gdje ili dodajemo ili oduzimamo diskriminanta)
Moramo pronaći najveći negativni korijen! Jasno je da je potrebno srediti.
Prvo razmotrite prvu seriju:
Jasno je da ako uzmemo, onda ćemo kao rezultat dobiti pozitivne brojeve, a oni nas ne zanimaju.
Dakle, morate to uzeti negativno. Neka.
Kada je root već:
I moramo pronaći najveći negativan!! To znači da više nema smisla ići u negativnom smjeru. I najveći negativni korijen za ovu seriju će biti.
Pogledajmo sada drugu seriju:
I opet zamjenjujemo:, zatim:
Nezainteresovan!
Onda više nema smisla povećavati! Smanjit ćemo! Neka onda:
Odgovara!
Neka. Onda
Zatim - najveći negativni korijen!
odgovor:
Problem broj 2
Opet rješavamo, bez obzira na kompleksni kosinus argument:
Sada ponovo izražavamo lijevo:
Obe strane množimo sa
Podijelimo obje strane na
Ostaje samo da ga pomerite udesno, menjajući njegov predznak sa minusa na plus.
Opet imamo 2 serije korijena, jedan sa i drugi sa.
Moramo pronaći najveći negativni korijen. Razmotrite prvu seriju:
Jasno je da ćemo dobiti prvi negativni korijen u, on će biti jednak i bit će najveći negativni korijen u 1 seriji.
Za drugu seriju
Prvi negativni korijen će se također dobiti na i bit će jednak. Budući da je tada najveći negativni korijen jednadžbe.
odgovor: .
Problem broj 3
Riješite bez obzira na kompleksni argument tangente.
Čini se da to nije ništa komplikovano, zar ne?
Kao i ranije, na lijevoj strani izražavamo:
Pa to je super, ovdje je samo jedan niz korijena! Ponovo pronađite najveći negativan.
Jasno je da ispada ako stavimo. I ovaj korijen je jednak.
odgovor:
Sada pokušajte sami riješiti sljedeće probleme.
Domaći zadatak ili 3 zadatka za samostalno rješenje.
- Odluke-shi-te jednadžba.
- Odluke-shi-te jednadžba.
U ot-ve-one na-pi-shi-te, najmanji po-li-tel-root. - Odluke-shi-te jednadžba.
U ot-ve-one na-pi-shi-te, najmanji po-li-tel-root.
Spreman? Provjeravam. Neću detaljno opisivati cijeli algoritam rješenja, čini mi se da mu je već gore posvećeno dovoljno pažnje.
Pa, je li sve u redu? Oh, ti gadni sinusi, s njima uvijek ima problema!
Pa, sada možete riješiti najjednostavnije trigonometrijske jednadžbe!
Provjerite rješenja i odgovore:
Problem broj 1
Hajde da izrazimo
Najmanji pozitivni korijen se dobija ako stavimo, pošto, onda
odgovor:
Problem broj 2
Najmanji pozitivni korijen se dobije kada.
Biće jednako.
odgovor: .
Problem broj 3
Kad stignemo, kad stignemo.
odgovor: .
Ovo znanje će vam pomoći da riješite mnoge probleme sa kojima ćete se suočiti na ispitu.
Ako se prijavljujete za ocjenu "5", onda samo trebate prijeći na čitanje članka srednji nivo, koji će biti posvećen rješavanju složenijih trigonometrijskih jednačina (zadatak C1).
PROSJEČAN NIVO
U ovom članku ću opisati rješavanje trigonometrijskih jednačina složenijeg tipa i kako odabrati njihove korijene. Ovdje ću se nadovezati na sljedeće teme:
- Trigonometrijske jednadžbe za početni nivo (vidi gore).
Složenije trigonometrijske jednadžbe su osnova složenijih problema. U njima je potrebno i riješiti samu jednačinu u općem obliku i pronaći korijene ove jednačine koji pripadaju određenom specificiranom intervalu.
Rješavanje trigonometrijskih jednadžbi svodi se na dva podzadatka:
- Rješenje jednadžbe
- Odabir korijena
Treba napomenuti da ovo drugo nije uvijek potrebno, ali je ipak potreban odabir u većini primjera. A ako nije potrebno, onda možete radije suosjećati - to znači da je jednadžba sama po sebi prilično komplicirana.
Moje iskustvo u raščlanjivanju C1 zadataka pokazuje da se oni obično dijele u ove kategorije.
Četiri kategorije zadataka povećane složenosti (ranije C1)
- Jednačine koje se svode na faktorizaciju.
- Jednačine se svode na oblik.
- Jednačine riješene promjenom varijable.
- Jednačine koje zahtijevaju dodatni odabir korijena zbog iracionalnosti ili nazivnika.
Jednostavno rečeno: ako naiđete jedna od prve tri vrste jednadžbi onda smatraj da si srecan. Za njih, u pravilu, dodatno morate pokupiti korijene koji pripadaju određenom intervalu.
Ako naiđete na jednadžbu tipa 4, onda ste manje sretni: morate se pozabaviti s njom malo duže i pažljivije, ali prilično često ne zahtijeva dodatni odabir korijena u njoj. Ipak, ovu vrstu jednadžbi ću analizirati u sljedećem članku, a ovaj će biti posvećen rješavanju jednačina prve tri vrste.
Faktoring Equations
Najvažnija stvar koju treba zapamtiti da biste riješili jednadžbe ovog tipa je
Kao što praksa pokazuje, ovo znanje je u pravilu dovoljno. Pogledajmo neke primjere:
Primjer 1. Svođenje jednadžbe na faktorizaciju korištenjem redukcijskih formula i sinusa dvostrukog ugla
- Res-shi-te jednadžba
- Ne-di-te svi korijeni ove jednadžbe
Ovdje, kao što sam obećao, formule za odbacivanje rade:
Tada će moja jednadžba izgledati ovako:
Tada će moja jednadžba poprimiti sljedeći oblik:
Kratkovid student bi mogao reći: a sad ću skratiti oba dijela, dobiti najjednostavniju jednačinu i uživati u životu! I bit će gorka pogrešna!
| ZAPAMTITE: NIKADA NEMOJTE SMANJIVATI OBA DIJELA TRIGONOMETRIJSKE JEDNAČINE ZA FUNKCIJU KOJA SADRŽI NEPOZNATO! TAKO GUBITE KORIJENJE! |
Pa šta ti radiš? Da, sve je jednostavno, pomaknite sve u jednom smjeru i izvadite zajednički faktor:
Pa, činimo to u faktore, ura! Sada odlučujemo:
Prva jednadžba ima korijene:
i drugi:
Ovim je završen prvi dio problema. Sada moramo odabrati korijene:
Razmak je ovakav:
Ili se može napisati i ovako:
Pa, hajde da uzmemo korene:
Prvo, poradimo na prvoj seriji (a lakše je, šta reći!)
Pošto je naš interval u potpunosti negativan, nema potrebe uzimati nenegativne, svejedno će dati nenegativne korijene.
Uzmimo, onda - malo previše, ne odgovara.
Neka, onda - nije udario ponovo.
Još jedan pokušaj - onda - tu je, pogodak! Prvi korijen pronađen!
Opet pucam: onda - opet sam pogodio!
Pa, još jednom:: - ovo je već let.
Dakle, iz prve serije 2 korijena pripadaju intervalu:.
Radimo sa drugom serijom (gradimo do stepena prema pravilu):
Undershoot!
Opet pothvat!
Opet pothvat!
Imam ga!
Let!
Dakle, sljedeći korijeni pripadaju mom rasponu:
Ovim algoritmom ćemo riješiti sve ostale primjere. Vježbajmo zajedno sa još jednim primjerom.
Primjer 2. Jednačina koja se svodi na faktorizaciju korištenjem redukcijskih formula
- Riješite jednačinu
Rješenje:
Opet zloglasne formule za lijevanje:
Opet, ne pokušavajte smanjiti!
Prva jednadžba ima korijene:
i drugi:
Sada ponovo tražite korijene.
Počeću sa drugom serijom, već znam sve o njoj iz prethodnog primera! Pogledajte i uvjerite se da su korijeni koji pripadaju praznini sljedeći:
Sada prva epizoda i jednostavnija je:
Ako - odgovara
Ako - je takođe dobro
Ako - već let.
Tada će korijeni biti sljedeći:
Samostalan rad. 3 jednadžbe.
Pa, da li ti je tehnika jasna? Rješavanje trigonometrijskih jednačina više ne izgleda tako teško? Zatim brzo sami riješite sljedeće probleme, a onda ćemo ti i ja riješiti druge primjere:
- Riješite jednačinu
Ne-di-to su svi korijeni ove jednadžbe, vezani za interval. - Res-shi-te jednadžba
Označite korijene jednačine - Res-shi-te jednadžba
Ne-di-to su svi korijeni ove jednadžbe-non-niy, priključeni-over-le-zha-shi-pro-me-zhut-ku.
Jednačina 1.
I opet formula za livenje:
Prva serija korijena:
Druga serija korijena:
Početak odabira za prazninu
Odgovor: , .
Jednačina 2. Provjera samostalnog rada.
Prilično zeznuto grupisanje u faktore (koristit ću formulu dvostrukog ugla sinusa):
onda ili
Ovo je opće rješenje. Sada moramo odabrati korijene. Problem je u tome što ne možemo reći tačnu vrijednost ugla čiji je kosinus jednak jednoj četvrtini. Stoga, ne mogu se tek tako riješiti arkosinusa - ovo je prava šteta!
Ono što mogu da uradim je da shvatim šta pa kako onda.
Napravimo tabelu: interval:
Pa, kroz bolna pretraživanja, došli smo do razočaravajućeg zaključka da naša jednadžba ima jedan korijen u naznačenom intervalu: \ displaystyle arccos \ frac (1) (4) -5 \ pi
Jednačina 3. Provjera samostalnog rada.
Zastrašujuća jednačina. Međutim, to se može riješiti vrlo jednostavno primjenom formule dvostrukog ugla sinusa:
Smanji za 2:
Grupirajmo prvi član sa drugim, a treći sa četvrtim i izvadimo zajedničke faktore:
Jasno je da prva jednadžba nema korijena, a sada razmotrite drugu:
Općenito, htio sam se malo kasnije zadržati na rješenju takvih jednadžbi, ali pošto se pokazalo, onda nema šta da se radi, potrebno je riješiti ...
Jednačine oblika:
Ova jednačina se rješava dijeljenjem oba dijela sa:
Dakle, naša jednadžba ima jednu seriju korijena:
Potrebno je pronaći one od njih koji pripadaju intervalu:.
Hajde da ponovo napravimo tabelu, kao što sam uradio ranije:
Odgovor: .
Jednačine koje se svode na oblik:
E, sad je vrijeme da pređemo na drugu grupu jednačina, pogotovo što sam već probrbljao od čega se sastoji rješenje trigonometrijskih jednačina novog tipa. Ali neće biti suvišno ponoviti tu jednačinu oblika
Rješava se dijeljenjem oba dijela kosinusom:
- Res-shi-te jednadžba
Navedite korijene jednadžbe-ne-nia, kada-preko-leže-od-rezanja. - Res-shi-te jednadžba
Navedite korijene jednadžbe-ne-nia, when-over-le-zha-shi-pro-me-zhut-ku.
Primjer 1.
Prvi je vrlo jednostavan. Pomaknite se udesno i primijenite formulu kosinusa dvostrukog ugla:
Aha! Jednačina oblika:. Oba dela delim na
Radimo prosijavanje korijena:
jaz:
odgovor:
Primjer 2.
Sve je također prilično trivijalno: proširimo zagrade na desnoj strani:
Osnovni trigonometrijski identitet:
Dvostruki ugaoni sinus:
Konačno dobijamo:
Ispadanje korijena: jaz.
Odgovor: .
Pa, kako vam se sviđa tehnika, nije previše komplikovana? Nadam se da ne. Odmah možemo napraviti rezervu: u svom čistom obliku, jednadžbe, koje se odmah svode na jednadžbu za tangentu, prilično su rijetke. Tipično, ovaj prijelaz (podjela kosinusom) je samo dio složenijeg problema. Evo primjera za vježbanje:
- Res-shi-te jednadžba
- Ne-di-to su svi korijeni ove jednadžbe-ne-nia, pričvršćene-nad-le-zha-shi-ku.
hajde da proverimo:
Jednačina se odmah rješava, dovoljno je oba dijela podijeliti na:
Otpadanje korijena:
Odgovor: .
Na ovaj ili onaj način, tek treba da se sretnemo sa jednačinama koje smo upravo analizirali. Međutim, još je rano da zaokružujemo: postoji još jedan "sloj" jednačina koji nismo analizirali. dakle:
Rješavanje trigonometrijskih jednadžbi promjenom varijable
Ovdje je sve transparentno: pažljivo promatramo jednačinu, pojednostavljujemo je što je više moguće, vršimo zamjenu, rješavamo, vršimo obrnutu zamjenu! Riječima, sve je vrlo lako. Da vidimo na djelu:
Primjer.
- Riješite jednačinu:.
- Ne-di-to su svi korijeni ove jednadžbe-ne-nia, pričvršćene-nad-le-zha-shi-ku.
Pa, evo i sama zamjena moli da bude u našim rukama!
Tada će se naša jednačina pretvoriti u ovo:
Prva jednadžba ima korijene:
A drugo je ovo:
Sada ćemo pronaći korijene koji pripadaju intervalu
Odgovor: .
Idemo zajedno na malo složeniji primjer:
- Res-shi-te jednadžba
- Navedite korijene date jednadžbe-non-niy, when-over-le-za-shi-n-e-zhut-ku.
Ovdje zamjena nije odmah vidljiva, štoviše, nije baš očigledna. Hajde da prvo razmislimo: šta možemo učiniti?
Na primjer, možemo zamisliti
I u isto vreme
Tada će moja jednadžba poprimiti oblik:
Sada pažnja, fokus:
Podijelimo obje strane jednačine sa:
Odjednom smo ti i ja dobili kvadratnu jednačinu za! Napravimo zamjenu, tada dobijamo:
Jednačina ima sljedeće korijene:
Gadna druga serija rootova, ali ne može se pomoći! Odabiremo korijene u intervalu.
To također moramo uzeti u obzir
Od i tada
odgovor:
Za konsolidaciju, prije nego što sami riješite probleme, evo još jedne vježbe za vas:
- Res-shi-te jednadžba
- Ne-di-to su svi korijeni ove jednadžbe-non-niy, priključeni-over-le-zha-shi-pro-me-zhut-ku.
Ovdje morate držati oči otvorene: sada imamo nazivnike koji mogu biti nula! Stoga, morate biti posebno pažljivi na korijene!
Prije svega, moram transformirati jednačinu tako da mogu napraviti odgovarajuću zamjenu. Trenutno ne mogu smisliti ništa bolje nego da prepišem tangentu u smislu sinusa i kosinusa:
Sada ću ići od kosinusa do sinusa prema osnovnom trigonometrijskom identitetu:
I na kraju, sve ću dovesti do zajedničkog imenioca:
Sada mogu da pređem na jednačinu:
Ali at (to jest, at).
Sada je sve spremno za zamjenu:
Onda bilo
Međutim, imajte na umu da ako, onda u isto vrijeme!
Ko pati od ovoga? Problem sa tangentom, ona je nedefinisana kada je kosinus nula (deljenje sa nulom).
Dakle, korijeni jednadžbe su sljedeći:
Sada izvlačimo korijene u intervalu:
| - odgovara | |
| - gruba sila |
Dakle, naša jednadžba ima jedan korijen u intervalu i jednaka je.
Vidite: pojava nazivnika (kao i tangente, dovodi do određenih poteškoća s korijenima! Ovdje morate biti oprezniji!).
Pa, ti i ja smo skoro završili analizu trigonometrijskih jednačina, ostalo je jako malo - da samostalno riješimo dva problema. Evo ih.
- Riješite jednačinu
Ne-di-to su svi korijeni ove jednadžbe-ne-nia, pričvršćene-nad-le-zha-shi-ku. - Res-shi-te jednadžba
Označite korijene ove jednadžbe, pričvršćene za rez.
Odlučili? Nije teško? hajde da proverimo:
- Radimo prema formulama redukcije:
Zamijenite u jednačinu:
Prepišimo sve u smislu kosinusa, tako da je zgodnije izvršiti zamjenu:
Sada je lako izvršiti zamjenu:
Jasno je da se radi o stranom korijenu, budući da jednačina nema rješenja. onda:
Tražimo korijene koji su nam potrebni u intervalu
Odgovor: .
Ovdje je zamjena odmah vidljiva:Onda bilo
- odgovara! - odgovara! - odgovara! - odgovara! - puno! - takođe puno! odgovor:
Pa, to je to! Ali rješavanje trigonometrijskih jednadžbi se tu ne završava, ostaju nam najteži slučajevi: kada postoji iracionalnost u jednadžbama ili razne vrste „složenih nazivnika“. Razmotrit ćemo kako riješiti takve zadatke u članku za napredni nivo.
NAPREDNI NIVO
Uz trigonometrijske jednadžbe o kojima se raspravljalo u prethodna dva članka, razmotrit ćemo još jednu klasu jednačina koje zahtijevaju još pažljiviju analizu. Ovi trigonometrijski primjeri sadrže ili iracionalnost ili nazivnik, što ih čini težim za analizu.... Međutim, možda ćete naići na ove jednadžbe u dijelu C ispitnog rada. Međutim, postoji srebrna podloga: za takve jednačine se u pravilu ne postavlja pitanje koji od njegovih korijena pripada datom intervalu. Hajde da ne lupamo okolo, nego samo trigonometrijske primjere.
Primjer 1.
Riješite jednačinu i pronađite korijene koji pripadaju segmentu.
Rješenje:
Imamo imenilac koji ne bi trebao biti nula! Tada je rješavanje ove jednačine isto kao i rješavanje sistema
Rešimo svaku od jednačina:
A sada drugo:
A sada da pogledamo seriju:
Jasno je da nam opcija ne odgovara, jer je u ovom slučaju imenilac nula (pogledajte formulu za korijene druge jednadžbe)
Ako je, međutim, onda je sve u redu, a imenilac nije nula! Tada su korijeni jednadžbe sljedeći:,.
Sada biramo korijene koji pripadaju intervalu.
| - ne odgovara | - odgovara | |
| - odgovara | - odgovara | |
| brute force | brute force |
Tada su korijeni sljedeći:
Vidite, čak i pojava malog šuma u obliku nazivnika značajno je utjecala na rješenje jednačine: ispustili smo niz korijena koji nula nazivnik. Situacija može biti još teža ako naiđete na trigonometrijske primjere koji imaju iracionalnost.
Primjer 2.
Riješite jednačinu:
Rješenje:
Pa, barem nema potrebe za odabirom korijena, i to je dobro! Hajde da prvo riješimo jednačinu, bez obzira na iracionalnost:
Da li je to sve? Ne, avaj, bilo bi previše lako! Mora se imati na umu da samo nenegativni brojevi mogu biti ispod korijena. onda:
Rješenje ove nejednakosti:
Sada ostaje da saznamo da li je neki od korena prve jednadžbe slučajno dospeo tamo gde nejednakost nije zadovoljena.
Da biste to učinili, ponovo možete koristiti tabelu:
| : , ali | Ne! | |
| Da! | ||
| Da! |
Tako mi je "ispao" jedan koren! Ispada ako ga stavite. Tada se odgovor može napisati na sljedeći način:
odgovor:
Vidite, korijen zahtijeva još veću pažnju! Da zakomplikujemo stvar: dozvolite mi sada da imam trigonometrijsku funkciju ispod korijena.
Primjer 3.
Kao i do sada: prvo ćemo riješiti svako posebno, a onda ćemo razmisliti šta smo uradili.
Sada druga jednadžba:
Sada je najteže saznati da li se negativne vrijednosti ispod aritmetičkog korijena dobivaju ako tamo zamijenimo korijene iz prve jednadžbe:
Broj treba shvatiti kao radijane. Pošto su radijani oko stepeni, radijani su oko stepeni. Ovo je ugao druge četvrtine. Koji je znak kosinusa druge četvrtine? Oduzeti. A sinus? A plus. Dakle, šta se može reći o izrazu:
Manje je od nule!
To znači da to nije korijen jednačine.
Sada je red.
Uporedimo ovaj broj sa nulom.
Kotangens je funkcija koja se smanjuje za 1 četvrtinu (što je manji argument, veći je kotangens). radijani su otprilike stepeni. U isto vrijeme
od tada i otuda
,
Odgovor: .
Može li biti još teže? Nema na čemu! Biće teže ako je trigonometrijska funkcija još uvijek ispod korijena, a drugi dio jednadžbe je opet trigonometrijska funkcija.
Što više trigonometrijskih primjera, to bolje, pogledajte dalje:
Primjer 4.
Korijen nije prikladan zbog ograničenog kosinusa
sad drugo:
Istovremeno, po definiciji korijena:
Moramo zapamtiti jedinični krug: naime, one četvrtine gdje je sinus manji od nule. Koje su to četvrti? Treći i četvrti. Tada će nas zanimati ona rješenja prve jednačine koja se nalaze u trećoj ili četvrtoj četvrtini.
Prva serija daje korijene na sjecištu treće i četvrte četvrtine. Druga serija, koja je dijametralno suprotna od njega, daje korijene koji leže na granici prve i druge četvrtine. Stoga nam ova serija ne odgovara.
Odgovor: ,
I opet trigonometrijski primjeri sa "teškom iracionalnošću"... Ne samo da opet imamo trigonometrijsku funkciju pod korijenom, već je sada i u nazivniku!
Primjer 5.
Pa ništa se ne može - ponašamo se kao i pre.
Sada radimo sa imeniocem:
Ne želim da rješavam trigonometrijsku nejednakost i zato ću postupiti lukavo: uzet ću i zamijeniti svoj niz korijena u nejednakosti:
Ako je - čak, onda imamo:
pošto, onda svi uglovi gledanja leže u četvrtoj četvrtini. I opet sveto pitanje: šta je sinusni znak u četvrtoj četvrtini? Negativno. Zatim nejednakost
Ako je čudno, onda:
U kojoj četvrtini leži ugao? Ovo je ugao druge četvrtine. Tada su svi uglovi opet uglovi druge četvrtine. Sinus je tamo pozitivan. Baš ono što vam treba! Dakle, serija:
Odgovara!
Pozabavite se drugom serijom korijena na isti način:
Zamjenjujemo u našoj nejednakosti:
Ako - čak, onda
Uglovi prve četvrtine. Sinus je tamo pozitivan, tako da je serija prikladna. Sada ako je - neparno, onda:
takođe odgovara!
Pa, sada zapisujemo odgovor!
odgovor:
Pa, ovo je možda bio slučaj koji je najviše oduzimao vrijeme. Sada vam nudim probleme za vaše rješenje.
Vježbati
- Riješite i pronađite sve korijene jednadžbe koji pripadaju segmentu.
rješenja:
Prva jednadžba:
ili
ODZ korijen:Druga jednačina:
Odabir korijena koji pripada praznini
odgovor:
Or
ili
Ali
Uzmite u obzir:. Ako - čak, onda
- ne odgovara!
Ako - neparno,: - odgovara!
To znači da naša jednadžba ima sljedeći niz korijena:
ili
Izbor korijena u intervalu:
| - ne odgovara | - odgovara | |
| - odgovara | - puno | |
| - odgovara | puno |
Odgovor: , .
Or
Od kada tangenta nije definirana. Odmah odbacujemo ovu seriju korijena!
drugi dio:
Istovremeno, prema ODZ-u, to je potrebno
Provjeravamo korijene pronađene u prvoj jednadžbi:
Ako je znak:
Uglovi prve četvrtine gdje je tangenta pozitivna. Ne odgovara!
Ako je znak:
Četvrti ugao. Tu je tangenta negativna. Odgovara. Zapisujemo odgovor:
Odgovor: , .
Zajedno smo pokrili složene trigonometrijske primjere u ovom članku, ali jednadžbe biste trebali riješiti sami.
SAŽETAK I OSNOVNE FORMULE
Trigonometrijska jednadžba je jednačina u kojoj je nepoznata striktno pod znakom trigonometrijske funkcije.
Postoje dva načina za rješavanje trigonometrijskih jednačina:
Prvi način je korištenje formula.
Drugi način je kroz trigonometrijski krug.
Omogućava vam mjerenje uglova, pronalaženje njihovih sinusa, kosinusa i još mnogo toga.
Priprema za profilni nivo jedinstvenog državnog ispita iz matematike. Korisni materijali o trigonometriji, velika teorijska video predavanja, video analize problema i izbor zadataka iz prošlih godina.
Korisni materijali
Video izbori i online kursevi
Trigonometrijske formule
Geometrijska ilustracija trigonometrijskih formula
Lučne funkcije. Najjednostavnije trigonometrijske jednadžbe
Trigonometrijske jednadžbe
- Potrebna teorija za rješavanje problema.
- a) Riješite jednačinu $ 7 \ cos ^ 2 x - \ cos x - 8 = 0 $.
b) Naći sve korijene ove jednačine koji pripadaju intervalu $ \ lijevo [- \ dfrac (7 \ pi) (2); - \ dfrac (3 \ pi) (2) \ desno] $. - a) Riješite jednačinu $ \ dfrac (6) (\ cos ^ 2 x) - \ dfrac (7) (\ cos x) + 1 = 0 $.
b) Naći sve korijene ove jednačine koji pripadaju intervalu $ \ lijevo [-3 \ pi; - \ pi \ desno] $. - Riješite jednačinu $ \ sin \ sqrt (16 - x ^ 2) = \ dfrac12 $.
- a) Riješite jednačinu $ 2 \ cos 2x - 12 \ cos x + 7 = 0 $.
b) Naći sve korijene ove jednačine koji pripadaju intervalu $ \ lijevo [- \ pi; \ dfrac (5 \ pi) (2) \ desno] $. - a) Riješite jednačinu $ \ dfrac (5) (\ mathrm (tg) ^ 2 x) - \ dfrac (19) (\ sin x) + 17 = 0 $.
- Riješite jednačinu $ \ dfrac (2 \ cos ^ 3 x + 3 \ cos ^ 2 x + \ cos x) (\ sqrt (\ mathrm (ctg) x)) = 0 $.
- Riješite jednačinu $ \ dfrac (\ mathrm (tg) ^ 3x - \ mathrm (tg) x) (\ sqrt (- \ sin x)) = 0 $.
b) Naći sve korijene ove jednačine koji pripadaju intervalu $ \ lijevo [- \ dfrac (5 \ pi) (2); - \ pi \ desno) $.- a) Riješite jednačinu $ \ cos 2x = \ sin \ lijevo (\ dfrac (3 \ pi) (2) - x \ desno) $.
b) Naći sve korijene ove jednačine koji pripadaju intervalu $ \ lijevo [\ dfrac (3 \ pi) (2); \ dfrac (5 \ pi) (2) \ desno] $. - a) Riješite jednačinu $ 2 \ sin ^ 2 \ lijevo (\ dfrac (3 \ pi) (2) + x \ desno) = \ sqrt3 \ cos x $.
b) Naći sve korijene ove jednačine koji pripadaju intervalu $ \ lijevo [- \ dfrac (7 \ pi) (2); -2 \ pi \ desno] $.
Video analiza zadataka
b) Naći sve korijene ove jednačine koji pripadaju segmentu $ \ left [\ sqrt (3); \ sqrt (20) \ desno] $.
b) Naći sve korijene ove jednačine koji pripadaju segmentu $ \ left [- \ dfrac (9 \ pi) (2); -3 \ pi \ desno] $.
b) Naći sve korijene ove jednačine koji pripadaju segmentu $ \ left [- \ sqrt (3); \ sqrt (30) \ desno] $.
a) Riješite jednačinu $ \ cos 2x = 1 - \ cos \ lijevo (\ dfrac (\ pi) (2) - x \ desno) $.
b) Naći sve korijene ove jednačine koji pripadaju intervalu $ \ lijevo [- \ dfrac (5 \ pi) (2); - \ pi \ desno) $.
a) Riješite jednačinu $ \ cos ^ 2 (\ pi - x) - \ sin \ lijevo (x + \ dfrac (3 \ pi) (2) \ desno) = 0 $.
b) Naći sve korijene ove jednačine koji pripadaju intervalu $ \ lijevo [\ dfrac (5 \ pi) (2); 4 \ pi \ desno] $.
b) Pronađite sve korijene ove jednačine koji pripadaju intervalu $ \ lijevo [\ log_5 2; \ log_5 20 \ desno] $.
a) Riješite jednačinu $ 8 \ sin ^ 2 x + 2 \ sqrt (3) \ cos \ lijevo (\ dfrac (3 \ pi) (2) - x \ desno) = 9 $.
b) Naći sve korijene ove jednačine koji pripadaju intervalu $ \ lijevo [- \ dfrac (5 \ pi) (2); - \ pi \ desno] $.
a) Riješite jednačinu $ 2 \ log_3 ^ 2 (2 \ cos x) - 5 \ log_3 (2 \ cos x) + 2 = 0 $.
b) Naći sve korijene ove jednačine koji pripadaju intervalu $ \ lijevo [\ pi; \ dfrac (5 \ pi) (2) \ desno] $.
a) Riješite jednačinu $ \ lijevo (\ dfrac (1) (49) \ desno) ^ (\ sin x) = 7 ^ (2 \ sin 2x) $.
b) Naći sve korijene ove jednačine koji pripadaju intervalu $ \ lijevo [\ dfrac (3 \ pi) (2); 3 \ pi \ desno] $.
a) Riješite jednačinu $ \ sin x + \ lijevo (\ cos \ dfrac (x) (2) - \ sin \ dfrac (x) (2) \ desno) \ lijevo (\ cos \ dfrac (x) (2)) + \ sin \ dfrac (x) (2) \ desno) = 0 $.
b) Naći sve korijene ove jednačine koji pripadaju intervalu $ \ lijevo [\ pi; \ dfrac (5 \ pi) (2) \ desno] $.
a) Riješite jednačinu $ \ log_4 (\ sin x + \ sin 2x + 16) = 2 $.
b) Naći sve korijene ove jednačine koji pripadaju intervalu $ \ lijevo [-4 \ pi; - \ dfrac (5 \ pi) (2) \ desno] $.
Izbor zadataka iz prethodnih godina
- a) Riješite jednačinu $ \ dfrac (\ sin x) (\ sin ^ 2 \ dfrac (x) (2)) = 4 \ cos ^ 2 \ dfrac (x) (2) $.
b) Naći sve korijene ove jednačine koji pripadaju segmentu $ \ left [- \ dfrac (9 \ pi) (2); -3 \ pi \ desno] $. (USE-2018. Rani talas) - a) Riješite jednačinu $ \ sqrt (x ^ 3 - 4x ^ 2 - 10x + 29) = 3 - x $.
b) Naći sve korijene ove jednačine koji pripadaju segmentu $ \ left [- \ sqrt (3); \ sqrt (30) \ desno] $. (USE-2018. Rani talas, rezervni dan) - a) Riješite jednačinu $ 2 \ sin ^ 2 x + \ sqrt2 \ sin \ lijevo (x + \ dfrac (\ pi) (4) \ desno) = \ cos x $.
b) Naći sve korijene ove jednačine koji pripadaju segmentu $ \ lijevo [-2 \ pi; - \ dfrac (\ pi) (2) \ desno] $. (USE-2018. Glavni val) - a) Riješite jednačinu $ \ sqrt6 \ sin ^ 2 x + \ cos x = 2 \ sin \ lijevo (x + \ dfrac (\ pi) (6) \ desno) $.
b) Naći sve korijene ove jednačine koji pripadaju segmentu $ \ lijevo [3 \ pi; \ dfrac (9 \ pi) (2) \ desno] $. (USE-2018. Glavni val) - a) Riješite jednačinu $ \ sin x + 2 \ sin \ lijevo (2x + \ dfrac (\ pi) (6) \ desno) = \ sqrt3 \ sin 2x + 1 $.
b) Naći sve korijene ove jednačine koji pripadaju segmentu $ \ left [- \ dfrac (7 \ pi) (2); -2 \ pi \ desno] $. (USE-2018. Glavni val) - a) Riješite jednačinu $ \ cos ^ 2 x + \ sin x = \ sqrt2 \ sin \ lijevo (x + \ dfrac (\ pi) (4) \ desno) $.
b) Naći sve korijene ove jednačine koji pripadaju segmentu $ \ lijevo [-4 \ pi; - \ dfrac (5 \ pi) (2) \ desno] $. (USE-2018. Glavni val) - a) Riješite jednačinu $ 2 \ sin \ lijevo (2x + \ dfrac (\ pi) (3) \ desno) - \ sqrt (3) \ sin x = \ sin 2x + \ sqrt3 $.
- a) Riješite jednačinu $ 2 \ sqrt3 \ sin \ lijevo (x + \ dfrac (\ pi) (3) \ desno) - \ cos 2x = 3 \ cos x - 1 $.
b) Naći sve korijene ove jednačine koji pripadaju segmentu $ \ lijevo [2 \ pi; \ dfrac (7 \ pi) (2) \ desno] $. (USE-2018. Glavni val) - a) Riješite jednačinu $ 2 \ sin \ lijevo (2x + \ dfrac (\ pi) (6) \ desno) - \ cos x = \ sqrt3 \ sin 2x - 1 $.
b) Naći sve korijene ove jednačine koji pripadaju segmentu $ \ left [\ dfrac (5 \ pi) (2); 4 \ pi \ desno] $. (USE-2018. Glavni val) - a) Riješite jednačinu $ \ sqrt2 \ sin \ lijevo (\ dfrac (\ pi) (4) + x \ desno) + \ cos 2x = \ sin x - 1 $.
b) Naći sve korijene ove jednačine koji pripadaju segmentu $ \ left [\ dfrac (7 \ pi) (2); 5 \ pi \ desno] $. (USE-2018. Glavni val) - a) Riješite jednačinu $ \ sqrt2 \ sin \ lijevo (2x + \ dfrac (\ pi) (4) \ desno) + \ sqrt2 \ cos x = \ sin 2x - 1 $.
b) Naći sve korijene ove jednačine koji pripadaju segmentu $ \ left [- \ dfrac (5 \ pi) (2); - \ pi \ desno] $. (USE-2018. Glavni val) - a) Riješite jednačinu $ 2 \ sin \ lijevo (x + \ dfrac (\ pi) (3) \ desno) + \ cos 2x = \ sqrt3 \ cos x + 1 $.
b) Naći sve korijene ove jednačine koji pripadaju segmentu $ \ lijevo [-3 \ pi; - \ dfrac (3 \ pi) (2) \ desno] $. (USE-2018. Glavni val)
b) Naći sve korijene ove jednačine koji pripadaju segmentu $ \ lijevo [\ pi; \ dfrac (5 \ pi) (2) \ desno] $. (USE-2018. Glavni val)- a) Riješite jednačinu $ 2 \ sin \ lijevo (x + \ dfrac (\ pi) (4) \ desno) + \ cos 2x = \ sqrt2 \ cos x + 1 $.
b) Naći sve korijene ove jednačine koji pripadaju segmentu $ \ lijevo [\ pi; \ dfrac (5 \ pi) (2) \ desno] $. (USE-2018. Glavni talas, rezervni dan) - a) Riješite jednačinu $ 2 \ cos x - \ sqrt3 \ sin ^ 2 x = 2 \ cos ^ 3 x $.
b) Naći sve korijene ove jednačine koji pripadaju segmentu $ \ left [- \ dfrac (7 \ pi) (2); -2 \ pi \ desno] $. (USE-2018. Glavni talas, rezervni dan) - a) Riješite jednačinu $ 2 \ cos x + \ sin ^ 2 x = 2 \ cos ^ 3 x $.
b) Naći sve korijene ove jednačine koji pripadaju segmentu $ \ left [- \ dfrac (9 \ pi) (2); -3 \ pi \ desno] $. (USE-2018. Glavni talas, rezervni dan) - a) Riješite jednačinu $ 2 \ sqrt2 \ sin \ lijevo (x + \ dfrac (\ pi) (3) \ desno) + 2 \ cos ^ 2 x = 2 + \ sqrt6 \ cos x $.
b) Naći sve korijene ove jednačine koji pripadaju segmentu $ \ lijevo [-3 \ pi; - \ dfrac (3 \ pi) (2) \ desno] $. (USE-2018. Glavni talas, rezervni dan) - a) Riješite jednačinu $ x - 3 \ sqrt (x - 1) + 1 = 0 $.
b) Naći sve korijene ove jednačine koji pripadaju segmentu $ \ left [\ sqrt (3); \ sqrt (20) \ desno] $. (USE-2018. Glavni talas, rezervni dan) - a) Riješite jednačinu $ 2x \ cos x - 8 \ cos x + x - 4 = 0 $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ lijevo [- \ dfrac (\ pi) (2); \ \ pi \ desno] $. (USE-2017, glavni talas, rezervni dan) - a) Riješite jednačinu $ \ log_3 (x ^ 2 - 2x) = 1 $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ lijevo [\ log_2 0 (,) 2; \ \ log_2 5 \ desno] $. (USE-2017, glavni talas, rezervni dan) - a) Riješite jednačinu $ \ log_3 (x ^ 2 - 24x) = 4 $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ lijevo [\ log_2 0 (,) 1; \ 12 \ sqrt (5) \ desno] $. (USE-2017, glavni talas, rezervni dan) - a) Riješite jednačinu $ 0 (,) 4 ^ (\ sin x) + 2 (,) 5 ^ (\ sin x) = 2 $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ lijevo [2 \ pi; \ \ dfrac (7 \ pi) (2) \ desno] $. (USE-2017, glavni talas) - a) Riješite jednačinu $ \ log_8 \ lijevo (7 \ sqrt (3) \ sin x - \ cos 2x - 10 \ desno) = 0 $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ lijevo [\ dfrac (3 \ pi) (2); \ 3 \ pi \ desno] $. (USE-2017, glavni talas) - a) Riješite jednačinu $ \ log_4 \ lijevo (2 ^ (2x) - \ sqrt (3) \ cos x - 6 \ sin ^ 2 x \ desno) = x $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ lijevo [\ dfrac (5 \ pi) (2); \ 4 \ pi \ desno] $. (USE-2017, glavni talas) - a) Riješite jednačinu $ 2 \ log_2 ^ 2 \ lijevo (\ sin x \ desno) - 5 \ log_2 \ lijevo (\ sin x \ desno) - 3 = 0 $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ lijevo [- 3 \ pi; \ - \ dfrac (3 \ pi) (2) \ desno] $. (USE-2017, glavni talas) - a) Riješite jednačinu $ 81 ^ (\ cos x) - 12 \ cdot 9 ^ (\ cos x) + 27 = 0 $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ lijevo [- 4 \ pi; \ - \ dfrac (5 \ pi) (2) \ desno] $. (USE-2017, glavni talas) - a) Riješite jednačinu $ 8 ^ x - 9 \ cdot 2 ^ (x + 1) + 2 ^ (5 - x) = 0 $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ lijevo [\ log_5 2; \ \ log_5 20 \ desno] $. (USE-2017, rani talas) - a) Riješite jednačinu $ 2 \ log ^ 2_9 x - 3 \ log_9 x + 1 = 0 $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ lijevo [\ sqrt (10); \ \ sqrt (99) \ desno] $. (USE-2016, glavni talas, rezervni dan) - a) Riješite jednačinu $ 6 \ log ^ 2_8 x - 5 \ log_8 x + 1 = 0 $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ lijevo [2; \ 2 (,) 5 \ desno] $. (USE-2016, glavni talas, rezervni dan) - a) Riješite jednačinu $ \ sin 2x = 2 \ sin x + \ sin \ lijevo (x + \ dfrac (3 \ pi) (2) \ desno) + 1 $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ lijevo [-4 \ pi; \ - \ dfrac (5 \ pi) (2) \ desno] $. (USE-2016, glavni talas, rezervni dan) - a) Riješite jednačinu $ 2 \ cos ^ 2 x + 1 = 2 \ sqrt (2) \ cos \ lijevo (\ dfrac (3 \ pi) (2) - x \ desno) $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ lijevo [\ dfrac (3 \ pi) (2); \ 3 \ pi \ desno] $. (USE-2016, glavni talas) - a) Riješite jednačinu $ 2 \ log ^ 2_2 (2 \ cos x) - 9 \ log_2 (2 \ cos x) + 4 = 0 $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ lijevo [-2 \ pi; \ - \ dfrac (\ pi) (2) \ desno] $. (USE-2016, glavni talas) - a) Riješite jednačinu $ 8 ^ x - 7 \ cdot 4 ^ x - 2 ^ (x + 4) + 112 = 0 $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ lijevo [\ log_2 5; \ \ log_2 11 \ desno] $. (USE-2016, rani talas) - a) Riješite jednačinu $ \ cos 2x + \ cos ^ 2 \ lijevo (\ dfrac (3 \ pi) (2) - x \ desno) = 0,25 $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ lijevo [-4 \ pi; \ - \ dfrac (5 \ pi) (2) \ desno] $. (USE-2016, rani talas) - a) Riješite jednačinu $ \ dfrac (13 \ sin ^ 2 x - 5 \ sin x) (13 \ cos x + 12) = 0 $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ lijevo [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ desno] $. (USE-2016, rani talas) - a) Riješite jednačinu $ \ dfrac (\ sin2x) (\ sin \ lijevo (\ dfrac (7 \ pi) (2) - x \ desno)) = \ sqrt (2) $.
b) Označite korijene ove jednačine koji pripadaju segmentu $ \ lijevo $. (USE-2015, glavni talas) - a) Riješite jednačinu $ 4 \ sin ^ 2 x = \ mathrm (tg) x $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ lijevo [- \ pi; \ 0 \ desno] $. (USE-2015, glavni talas) - a) Riješite jednačinu $ 3 \ cos 2x - 5 \ sin x + 1 = 0 $.
b) Označite korijene ove jednačine koji pripadaju segmentu $ \ lijevo [\ pi; \ \ dfrac (5 \ pi) (2) \ desno] $. (USE-2015, glavni talas) - a) Riješite jednačinu $ \ cos 2x - 5 \ sqrt (2) \ cos x - 5 = 0 $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ lijevo [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ desno] $. (USE-2015, glavni talas) - a) Riješite jednačinu $ \ sin 2x + \ sqrt (2) \ sin x = 2 \ cos x + \ sqrt (2) $.
b) Označite korijene ove jednačine koji pripadaju segmentu $ \ lijevo [\ pi; \ \ dfrac (5 \ pi) (2) \ desno] $. (USE-2015, rani talas) - a) Riješite jednačinu $ 2 \ cos ^ 3 x - \ cos ^ 2 x + 2 \ cos x - 1 = 0 $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ lijevo [2 \ pi; \ \ dfrac (7 \ pi) (2) \ desno] $. (USE-2015, rani talas) - a) Riješite jednačinu $ \ mathrm (tg) ^ 2 x + (1 + \ sqrt (3)) \ mathrm (tg) x + \ sqrt (3) = 0 $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ left [\ dfrac (5 \ pi) (2); \ 4 \ pi \ desno] $. (USE-2014, glavni talas) - a) Riješite jednačinu $ 2 \ sqrt (3) \ cos ^ 2 \ lijevo (\ dfrac (3 \ pi) (2) + x \ desno) - \ sin 2x = 0 $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ left [\ dfrac (3 \ pi) (2); \ 3 \ pi \ desno] $. (USE-2014, glavni talas) - a) Riješite jednačinu $ \ cos 2x + \ sqrt (2) \ sin \ lijevo (\ dfrac (\ pi) (2) + x \ desno) + 1 = 0 $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ left [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ desno] $. (USE-2014, glavni talas) - a) Riješite jednačinu $ - \ sqrt (2) \ sin \ lijevo (- \ dfrac (5 \ pi) (2) + x \ desno) \ cdot \ sin x = \ cos x $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ left [\ dfrac (9 \ pi) (2); \ 6 \ pi \ desno] $. (USE-2014, rani talas) - a) Riješite jednačinu $ \ sin 2x = \ sin \ lijevo (\ dfrac (\ pi) (2) + x \ desno) $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ left [- \ dfrac (7 \ pi) (2); \ - \ dfrac (5 \ pi) (2) \ desno] $. (USE-2013, glavni talas) - a) Riješite jednačinu $ 6 \ sin ^ 2 x + 5 \ sin \ lijevo (\ dfrac (\ pi) (2) - x \ desno) - 2 = 0 $.
b) Navedite korijene ove jednačine koji pripadaju segmentu $ \ left [-5 \ pi; \ - \ dfrac (7 \ pi) (2) \ desno] $. (USE-2012, drugi talas)
Svrha lekcije:
a) učvrstiti sposobnost rješavanja najjednostavnijih trigonometrijskih jednačina;
b) naučiti birati korijene trigonometrijskih jednadžbi iz datog intervala
Tokom nastave.
1. Aktuelizacija znanja.
a) Provjera domaćeg zadatka: razred je dobio anticipativni domaći zadatak - riješiti jednačinu i pronaći način odabira korijena iz zadanog intervala.
1) cos x= -0,5, gdje je xI [-]. odgovor:.
2) grijeh x=, gdje je xI. Odgovor: ; ...
3) cos 2 x= -, gdje je hI. odgovor:
Učenici zapisuju rješenje na ploču, neko pomoću grafikona, neko metodom odabira.
U ovo vrijeme razred radi usmeno.
Pronađite značenje izraza:
a) tg - sin + cos + sin. Odgovor: 1.
b) 2arccos 0 + 3 arccos 1. Odgovor: ?
c) arcsin + arcsin. odgovor:.
d) 5 arctan (-) - arccos (-). Odgovor:-.
- Hajde da proverimo domaće zadatke, otvorimo sveske.
Neki od vas su pronašli rješenje metodom uklapanja, a neki grafom.
2. Zaključak o načinu rješavanja ovih zadataka i navod problema, odnosno poruka teme i svrha lekcije.
- a) Teško je riješiti uz pomoć selekcije ako je dat veliki interval.
- b) Grafička metoda ne daje tačne rezultate, zahtijeva provjeru i oduzima puno vremena.
- Dakle, mora postojati barem još jedna metoda, najuniverzalnija - hajde da je pokušamo pronaći. Dakle, šta ćemo danas raditi na času? (Naučite odabrati korijene trigonometrijske jednadžbe u datom intervalu.)
- Primjer 1 (Učenik ide do table)
cos x= -0,5, gdje je xI [-].
Pitanje: Od čega zavisi odgovor na ovaj zadatak? (Iz opšteg rešenja jednačine. Zapišimo rešenje u opštem obliku). Odluka je ispisana na tabli
h = + 2? k, gdje je k R.
- Zapišimo ovo rješenje u obliku skupa:

- Šta mislite, za koji zapis rješenja je zgodno odabrati korijene u intervalu? (iz drugog unosa). Ali ovo je opet metoda selekcije. Šta trebamo znati da bismo dobili pravi odgovor? (Morate znati vrijednosti k).
(Napravimo matematički model da pronađemo k).
pošto je kI Z, onda je k = 0, dakle X= = |
ova nejednakost pokazuje da ne postoje cjelobrojne vrijednosti k. |
zaključak: Da biste odabrali korijene iz zadanog intervala prilikom rješavanja trigonometrijske jednadžbe, trebate:
- da se reši jednačina oblika sin x = a, cos x = a zgodnije je zapisati korijene jednadžbe kao dvije serije korijena.
- za rješavanje jednačina oblika tg x = a, ctg x = a zapišite opću formulu za korijene.
- izraditi matematički model za svako rješenje u obliku dvostruke nejednakosti i pronaći cjelobrojnu vrijednost parametra k ili n.
- zamijenite ove vrijednosti u korijen formulu i izračunajte ih.
Rešiti primere 2 i 3 iz domaće zadaće koristeći dobijeni algoritam. Istovremeno, dva učenika rade za tablom, nakon čega slijedi provjera rada.
U ovom članku pokušat ću objasniti 2 načina izbor korijena u trigonometrijskoj jednadžbi: korištenjem nejednačina i korištenjem trigonometrijskog kruga. Idemo direktno na ilustrativni primjer i pozabavimo se slučajem.
A) Riješite jednačinu sqrt (2) cos ^ 2x = sin (Pi / 2 + x)
b) Pronađite sve korijene ove jednačine koji pripadaju intervalu [-7Pi / 2; -2Pi]
Hajde da rešimo tačku a.
Koristimo formulu redukcije za sinus sin (Pi / 2 + x) = cos (x)
Sqrt (2) cos ^ 2x = cosx
Sqrt (2) cos ^ 2x - cosx = 0
Cosx (sqrt (2) cosx - 1) = 0
X1 = Pi / 2 + Pin, n ∈ Z
Sqrt (2) cosx - 1 = 0
Cosx = 1 / sqrt (2)
Cosx = sqrt (2) / 2
X2 = arccos (sqrt (2) / 2) + 2Pin, n ∈ Z
x3 = -arccos (sqrt (2) / 2) + 2Pin, n ∈ Z
X2 = Pi / 4 + 2Pin, n ∈ Z
x3 = -Pi / 4 + 2Pin, n ∈ Z
Rešimo tačku b.
1) Odabir korijena korištenjem nejednačina
Ovdje se sve radi jednostavno, dobijene korijene zamjenjujemo u datom intervalu [-7Pi / 2; -2Pi], pronađite cjelobrojne vrijednosti za n.
7Pi / 2 manje ili jednako Pi / 2 + Pin manje ili jednako -2Pi
Podijelite sve na Pi odjednom
7/2 je manje ili jednako 1/2 + n je manje ili jednako -2
7/2 - 1/2 manje ili jednako n manje ili jednako -2 - 1/2
4 manje ili jednako n manje od ili jednako -5/2
Cijeli broj n u ovom rasponu je -4 i -3. Dakle, korijeni koji pripadaju ovom intervalu će biti Pi / 2 + Pi (-4) = -7Pi / 2, Pi / 2 + Pi (-3) = -5Pi / 2
Slično, pravimo još dvije nejednakosti
7Pi / 2 manje ili jednako Pi / 4 + 2Pin manje ili jednako -2Pi
-15/8 manje ili jednako n manje ili jednako -9/8
U ovom intervalu nema cijelog broja n
7Pi / 2 manje ili jednako -Pi / 4 + 2Pin manje ili jednako -2Pi
-13/8 manje ili jednako n manje ili jednako -7/8
Jedan cijeli broj n u ovom rasponu je -1. Dakle, odabrani korijen na ovom intervalu je -Pi / 4 + 2Pi * (- 1) = -9Pi / 4.
Dakle, odgovor u tački b: -7Pi / 2, -5Pi / 2, -9Pi / 4
2) Odabir korijena pomoću trigonometrijskog kruga
Da biste koristili ovu metodu, morate razumjeti kako ovaj krug funkcionira. Pokušat ću jednostavnim jezikom objasniti kako ovo razumijem. Mislim da se u školama na časovima algebre ova tema mnogo puta objašnjavala pametnim riječima nastavnika, složenim formulacijama u udžbenicima. Osobno, ovo razumijem kao krug koji se može prijeći beskonačan broj puta, zbog činjenice da su sinusne i kosinusne funkcije periodične.
Idemo jednom u smjeru suprotnom od kazaljke na satu
Idemo okolo 2 puta u smjeru suprotnom od kazaljke na satu
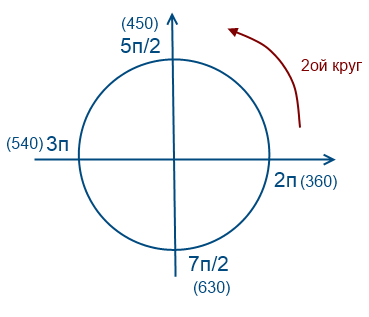
Idemo 1 put u smjeru kazaljke na satu (vrijednosti će biti negativne)

Vratimo se na naše pitanje, moramo odabrati korijene u intervalu [-7Pi / 2; -2Pi]
Da biste došli do brojeva -7Pi / 2 i -2Pi, trebate dva puta obići krug u smjeru suprotnom od kazaljke na satu. Da bi se pronašli korijeni jednadžbe na ovom intervalu, potrebno je procijeniti i zamijeniti.
Uzmimo x = Pi / 2 + Pin. Koja je približna vrijednost n da bi vrijednost x bila negdje u ovom intervalu? Zamjenom, recimo -2, dobijamo Pi / 2 - 2Pi = -3Pi / 2, očigledno ovo nije uključeno u naš interval, pa uzimamo manje od -3, Pi / 2 - 3Pi = -5Pi / 2, odgovara, hajde da probamo ponovo -4, Pi / 2 - 4Pi = -7Pi / 2 je takođe pogodan.
Slično razmišljajući za Pi / 4 + 2Pin i -Pi / 4 + 2Pin, nalazimo još jedan korijen -9Pi / 4.

Poređenje ove dvije metode.
Prva metoda (koristeći nejednakosti) je mnogo pouzdanija i mnogo lakša za razumijevanje, ali ako se zaista ozbiljno bavite trigonometrijskim krugom i drugom metodom odabira, tada će odabir korijena biti mnogo brži, možete uštedjeti oko 15 minuta na ispit.
a) Riješite jednačinu:.
b) Pronađite sve korijene ove jednačine koji pripadaju segmentu.
Rješenje problema

Ova lekcija razmatra primjer rješavanja trigonometrijske jednadžbe, koja se može koristiti kao primjer za rješavanje zadataka tipa C1 u pripremi za ispit iz matematike.
Prije svega, određuje se opseg funkcije - sve dozvoljene vrijednosti argumenta. Zatim, tokom rješavanja, trigonometrijska sinusna funkcija se pretvara u kosinus koristeći formulu redukcije. Dalje, svi članovi jednačine se prenose na njenu lijevu stranu, gdje je zajednički faktor uzet iz zagrada. Svaki faktor je postavljen jednak nuli, što vam omogućava da odredite korijene jednadžbe. Zatim se metodom zavoja određuju korijeni koji pripadaju datom segmentu. Da biste to učinili, petlja je označena na izgrađenom jediničnom krugu od lijeve granice navedenog segmenta na desno. Nadalje, pronađeni korijeni na jediničnom krugu povezani su segmentima s njegovim centrom i određuju se tačke u kojima ovi segmenti sijeku petlju. Ove tačke preseka su željeni odgovor na drugi deo problema.

































