Prava y = 3x + 2 tangenta je na graf funkcije y = -12x ^ 2 + bx-10. Naći b, s obzirom da je apscisa dodirne tačke manja od nule.

Pokaži rješenje

Rješenje

Neka je x_0 apscisa tačke na grafu funkcije y = -12x ^ 2 + bx-10, kroz koju prolazi tangenta na ovaj graf.

Vrijednost derivacije u tački x_0 jednaka je nagibu tangente, odnosno y"(x_0) = - 24x_0 + b = 3. S druge strane, tačka tangente pripada oba grafa funkcije i tangenta, odnosno -12x_0 ^ 2 + bx_0-10 = 3x_0 + 2. Dobijamo sistem jednadžbi \ početak (slučajevi) -24x_0 + b = 3, \\ - 12x_0 ^ 2 + bx_0-10 = 3x_0 + 2. \ kraj (slučajevi)

Rješavajući ovaj sistem, dobijamo x_0 ^ 2 = 1, što znači ili x_0 = -1, ili x_0 = 1. Prema uslovu, apscisa dodirne tačke je manja od nule, dakle x_0 = -1, zatim b = 3 + 24x_0 = -21.

Odgovori

Stanje

Na slici je prikazan grafik funkcije y = f (x) (koja je izlomljena linija sastavljena od tri pravolinijska segmenta). Koristeći sliku, izračunajte F (9) -F (5), gdje je F (x) jedan od antiderivata f (x).

Pokaži rješenje

Rješenje

Prema Newton-Leibnizovoj formuli, razlika F (9) -F (5), gdje je F (x) jedan od antiderivata funkcije f (x), jednaka je površini omeđenog krivolinijskog trapeza grafikom funkcije y = f (x), pravim linijama y = 0, x = 9 i x = 5. Prema grafu utvrđujemo da je navedeni zakrivljeni trapez trapez sa osnovama jednakim 4 i 3 i visinom 3.

Njegova površina je \ frac (4 + 3) (2) \ cdot 3 = 10,5.

Odgovori

Izvor: „Matematika. Priprema za ispit-2017. Nivo profila". Ed. FF Lysenko, S. Yu. Kulabukhova.

Stanje

Na slici je prikazan graf y = f "(x) - derivacije funkcije f (x), definisane na intervalu (-4; 10). Pronađite intervale opadanja funkcije f (x). odgovor, navedite dužinu najvećeg od njih.

Pokaži rješenje

Rješenje

Kao što znate, funkcija f (x) opada na tim intervalima, u čijoj je svakoj tački izvod f"(x) manji od nule. Uzimajući u obzir da je potrebno pronaći dužinu najvećeg od njih, tri takvi intervali se prirodno razlikuju od slike: (-4; -2) ; (0; 3); (5; 9).

Dužina najvećeg od njih - (5; 9) jednaka je 4.

Odgovori

Izvor: „Matematika. Priprema za ispit-2017. Nivo profila". Ed. FF Lysenko, S. Yu. Kulabukhova.

Stanje

Na slici je prikazan graf y = f "(x) - derivacije funkcije f (x), definisane na intervalu (-8; 7). Pronađite broj maksimalnih tačaka funkcije f (x) koji pripadaju interval [-6; -2].

Pokaži rješenje

Rješenje

Grafikon pokazuje da derivacija f"(x) funkcije f (x) mijenja predznak sa plusa na minus (u takvim tačkama će biti maksimum) u tačno jednoj tački (između -5 i -4) od interval [-6; -2 ] Dakle, postoji tačno jedna maksimalna tačka na intervalu [-6; -2].

Odgovori

Izvor: „Matematika. Priprema za ispit-2017. Nivo profila". Ed. FF Lysenko, S. Yu. Kulabukhova.

Stanje

Na slici je prikazan grafik funkcije y = f (x), definirane na intervalu (-2; 8). Odrediti broj tačaka u kojima je derivacija funkcije f (x) 0.

Pokaži rješenje

Rješenje

Jednakost derivacije sa nulom u tački znači da je tangenta na graf funkcije, nacrtana u ovoj tački, paralelna sa Ox osom. Dakle, nalazimo tačke u kojima je tangenta na graf funkcije paralelna sa Ox osom. Na ovom grafikonu takve tačke su ekstremne tačke (tačke maksimuma ili minimuma). Kao što vidite, postoji 5 ekstremnih tačaka.

Odgovori

Izvor: „Matematika. Priprema za ispit-2017. Nivo profila". Ed. FF Lysenko, S. Yu. Kulabukhova.

Stanje

Prava y = -3x + 4 je paralelna sa tangentom na graf funkcije y = -x ^ 2 + 5x-7. Pronađite apscisu dodirne tačke.

Pokaži rješenje

Rješenje

Nagib ravne na grafiku funkcije y = -x ^ 2 + 5x-7 u proizvoljnoj tački x_0 jednak je y "(x_0). Ali y" = - 2x + 5, tako da je y "(x_0 ) = - 2x_0 + 5. Ugaoni koeficijent prave y = -3x + 4 specificiran u uslovu je jednak -3. Paralelne prave imaju isti nagib. Dakle, nalazimo vrijednost x_0 takvu da je = -2x_0 + 5 = -3.

Dobijamo: x_0 = 4.

Odgovori

Izvor: „Matematika. Priprema za ispit-2017. Nivo profila". Ed. FF Lysenko, S. Yu. Kulabukhova.

Stanje

Na slici je prikazan grafik funkcije y = f (x), a tačke -6, -1, 1, 4 su označene na osi apscise. U kojoj od ovih tačaka je vrijednost derivacije najmanja? Navedite ovu tačku u svom odgovoru.

Majstorska klasa iz matematike

u 11 razredu

na ovu temu

"DERIVATNA FUNKCIJA

U ZADACI KORIŠĆENJA"

nastavnik matematike

Martynenko E.N.

2017-2018 akademska godina

Svrha majstorske klase: razvijati vještine učenikaprimjena teorijskih znanja na temu "Derivat funkcije" za rješavanje zadataka jedinstvenog državnog ispita.

Zadaci

edukativni:da sumira i sistematizuje znanja učenika o temi

„Derivat funkcije“, razmotriti prototipove USE problema na ovu temu, studentima pruža mogućnost da provjere svoje znanje prilikom samostalnog rješavanja problema.

u razvoju: promovirati razvoj pamćenja, pažnje, samopoštovanja i vještina samokontrole; formiranje osnovnih ključnih kompetencija (poređenje, jukstapozicija, klasifikacija objekata, određivanje adekvatnih načina za rješavanje obrazovnog problema na osnovu navedenih algoritama, sposobnost samostalnog djelovanja u situaciji neizvjesnosti, kontrola i evaluacija njihovih aktivnosti, pronalaženje i otkloniti uzroke nastalih poteškoća).

edukativni: promovirati:

Formiranje odgovornog odnosa prema učenju kod učenika;

razvijanje trajnog interesovanja za matematiku;

stvaranje pozitivne unutrašnje motivacije za učenje matematike.

Tehnologije: individualno diferencirano učenje, IKT.

Nastavne metode: verbalno, vizuelno, praktično, problematično.

Oblici rada: pojedinačno, frontalno, u parovima.

Oprema i materijal za nastavu:projektor, platno, računar, simulator(Dodatak br. 1), prezentacija za lekciju(Dodatak br. 2), individualno - diferencirane kartice za samostalan rad u parovima(Prilog br. 3), lista internet stranica, individualno diferencirani domaći zadaci(Dodatak br. 4).

Objašnjenje za majstorsku klasu.

Ova majstorska klasa se održava u 11. razredu radi pripreme za Jedinstveni državni ispit. Ima za cilj primjenu teorijskog materijala na temu "Derivat funkcije" u rješavanju ispitnih zadataka.

Trajanje majstorske klase- 20 minuta.

Struktura majstorske klase

I. Organizacioni momenat -1 min.

II Komunikacija teme, ciljevi master-klasa, motivacija obrazovnih aktivnosti - 1 min.

III. Frontalni rad. Obuka "Zadaci br. 14 BAZA, br. 7 PROFIL Jedinstvenog državnog ispita". Analiza rada sa simulatorom - 7 min.

IV.Individualno - diferencirani rad u parovima. Samostalno rješavanje zadataka br. 12. (PROFIL) Međusobna provjera - 9 min. On-line testiranje (BAZA) Analiza rezultata testa - 8 min

V. Provjera individualnog domaćeg zadatka. -1 minut.

Vi. Individualno - diferencirani domaći -1 min.

Vii. KONTROLNI TEST 20 MINUTA (4 OPCIJE)

Napredak majstorske klase

I .Organiziranje vremena.

II Komunikacija teme, ciljevi master-klasa, motivacija obrazovnih aktivnosti.

(Slajdovi 1-2, Dodatak #2)

Tema naše lekcije je "Izvod funkcije u ispitnim zadacima". Svi znaju za izreku “Mala kalem, ali draga”. Jedan od takvih „kalemova” u matematici je izvod. Izvod se koristi u rješavanju mnogih praktičnih problema iz matematike, fizike, hemije, ekonomije i drugih disciplina. Omogućava vam da probleme rješavate jednostavno, lijepo i zanimljivo.

Tema „Derivat“ je predstavljena u zadatku broj 14 osnovnog nivoa i zadacima nivoa profila br. 7,12, 18 i jedinstvenom državnom ispitu.

Radili ste sa dokumentima koji regulišu strukturu i sadržaj kontrolnih mjernih materijala Jedinstvenog državnog ispita iz matematike 2018. Donesite zaključak o tome koja su vam znanja i vještine potrebna za uspješno rješavanje EKS zadataka na temu „Izvod“.

(Slajdovi 3-4, Dodatak #2)

Jeste li naučili "Kodifikator elemenata sadržaja iz MATEMATIKE za pripremu kontrolnih mjernih materijala za jedinstveni državni ispit",

„Kodifikator uslova za stepen osposobljenosti diplomiranih studenata“, „Specifikacija kontrolnih mernih materijala“, „Demonstraciona verzija kontrolnih mernih materijala jedinstvenog državnog ispita 2018.“ i saznao koja znanja i vještine o funkciji i njenom derivatu su potrebna za uspješno rješavanje zadataka na temu "Izvod".

Neophodno

• KNOW

pravila obračuna izvedenica;

derivati ​​osnovnih elementarnih funkcija;

geometrijsko i fizičko značenje izvedenice;
jednadžba tangente na graf funkcije;
proučavanje funkcije koristeći derivaciju.

• BITI U mogućnosti

izvršiti radnje sa funkcijama (opisati ponašanje i svojstva funkcije prema grafu, pronaći njene najveće i najniže vrijednosti).

• KORISTI

stečena znanja i vještine u praksi i svakodnevnom životu.

Imate teorijsko znanje o temi Derivati. Danas ćemoNAUČITE DA PRIMJENITE ZNANJE O FUNKCIJI IZVODA ZA RJEŠAVANJE PROBLEMA UPOTREBE.(Slajd 4, Dodatak br. 2)

Nije uzalud Aristotel je to rekao“UM NIJE SAMO U ZNANJU, VEĆ I U SPOSOBNOSTI PRIMJENE ZNANJA U PRAKSI”(Slajd 5, Dodatak br. 2)

Na kraju lekcije vratit ćemo se cilju naše lekcije i saznati da li smo ga postigli?

III ... Frontalni rad.Obuka "Zadaci br. 14 BAZA br. 7 PROFIL Jedinstvenog državnog ispita" ( Dodatak br. 1). Analiza rada sa simulatorom.

Odaberite tačan odgovor od četiri predložena.

Šta je, po Vašem mišljenju, teško da se izvrši zadatak broj 7?

Šta mislite, koje su tipične greške koje maturanti prave na ispitu prilikom rješavanja ovog problema?

Prilikom odgovaranja na pitanja zadatka br. 14 BAZA I br. 7 PROFIL, morate znati opisati ponašanje i svojstva funkcije iz grafa derivacije, a iz grafa funkcije - ponašanje i svojstva funkcije. derivacija funkcije. A za to je potrebno dobro teorijsko znanje o sljedećim temama: „Geometrijsko i mehaničko značenje derivacije. Tangenta na graf funkcije. Primjena derivacije u proučavanju funkcija”.

Analizirajte koji su vam zadaci stvarali poteškoće?

Koja teorijska pitanja trebate znati?

IV. On - line testiranje na zadacima №14 (BAZA)Analiza rezultata ispitivanja.

Sajt za testiranje u lekciji:http://www.mathb-ege.sdamgia.ru/

Ko nije napravio greške?

Ko je imao poteškoća u testiranju? Zašto?

U kojim zadacima su napravljene greške?

Zaključite, koja teorijska pitanja trebate znati?

Individualno - diferencirani rad u parovima. Samostalno rješavanje zadataka №12. (PROFIL)Međusobna provjera.(Dodatak br. 3)

Prisjetite se algoritma za rješavanje zadataka №12 ispita za pronalaženje ekstremnih tačaka, ekstrema funkcije, najveće i najmanje vrijednosti funkcije na intervalu pomoću izvoda.

Riješite probleme s derivatom

Učenici se suočavaju sa problemom:

"Razmislite, da li je moguće riješiti neke probleme broj 12 na drugačiji način, bez upotrebe derivata?"

1 par

2 para

3 para

4 para

(Učenici brane svoje rješenje tako što na tabli ispisuju glavne korake za rješavanje problema. Učenici nude dva načina rješavanja problema br. 2).

Rješenje problema. Zaključak za studente:

"Neki problemi br. 12 na ispitu za pronalaženje najmanje i najveće vrijednosti funkcije mogu se riješiti bez korištenja izvoda, oslanjajući se na svojstva funkcija."

Analizirajte koju grešku ste napravili u zadatku?

Koja teorijska pitanja trebate ponoviti?

V. Provjera individualnog domaćeg zadatka. (Slajdovi 7-8, Dodatak br. 2)

Vegelman V. je dobio individualni domaći zadatak: iz priručnika za pripremu ispita broj 18.

(Student daje rješenje zadatka, oslanjajući se na funkcionalno-grafičku metodu, kao jednu od metoda za rješavanje zadataka br. 18 ispita i daje kratko objašnjenje ove metode).

Vii. Individualno - diferencirani domaći

(Slajd 9, Dodatak br. 2), (Dodatak br. 4).

Pripremio sam listu internet stranica za pripremu ispita. Na ovim stranicama također možete pristupiti on-line testiranju. Za sledeću lekciju potrebno je: 1) pregledati teorijski materijal na temu „Izvod funkcije“;

2) na sajtu "Otvorena banka zadataka iz matematike" (http://mathege.ru/ ) pronaći prototipove zadataka br. 14 BAZA I br. 7 i 12 PROFIL i riješiti najmanje 10 zadataka PROFIL;

3) V. Vegelman, riješi zadatke s parametrima (DODATAK 4). zadaci 1-8 (opcija 1).OSNOVNI NIVO

VIII. Ocjene na nastavi.

Kako biste sebe ocijenili za lekciju?

Mislite li da ste mogli bolje učiti na lekciji?

IX. Sažetak lekcije. Refleksija

Hajde da sumiramo naš rad. Šta je bila svrha lekcije? Mislite li da je to postignuto?

Pogledajte tablu i u jednoj rečenici, birajući početak fraze, nastavite onom rečenicom koja vam najviše odgovara.

Osjetio sam…

Naučio sam…

uspio sam…

Mogao sam...

Pokušat ću …

Bio sam iznenađen to …

htio sam…

Možete li reći da je tokom lekcije došlo do obogaćivanja vaših zaliha znanja?

Dakle, ponovili ste teorijska pitanja o derivaciji funkcije, primijenili svoja znanja u rješavanju prototipova USE zadataka (br. 14 OSNOVNI NIVO br. 7,12 PROFILNI NIVO), a V. Vegelman je završio zadatak br. 18 sa parametrom, što je zadatak povećanog stepena poteškoća.

Bilo mi je zadovoljstvo raditi sa vama i nadam se da ćete moći uspješno primijeniti stečeno znanje na časovima matematike ne samo prilikom polaganja Jedinstvenog državnog ispita, već i u daljem školovanju.

Hteo bih da završim lekciju rečima jednog italijanskog filozofaToma Akvinski"Znanje je toliko dragocjena stvar da ga nije sramota dobiti iz bilo kojeg izvora."(Slajd 10, Dodatak br. 2).

Želim vam uspjeh u pripremama za ispit!

Pregled:

Da biste koristili pregled prezentacija, kreirajte sebi Google račun (nalog) i prijavite se na njega: https://accounts.google.com

Naslovi slajdova:

Priprema za ispit SIMULATOR na temu "Derivat" Zadatak broj 14 osnovni nivo, broj 7, 12 profilni nivo

f (x) f / (x) x Na slici je prikazan grafik derivacije funkcije y = f (x), specificirane na intervalu (- 8; 8). Istražimo svojstva grafa i moći ćemo odgovoriti na mnoga pitanja o svojstvima funkcije, iako graf same funkcije nije predstavljen! y = f / (x) 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 4 3 2 1 -1 -2 -3 -4 -5 yx 6 3 0 -5 Pronađite bodove gdje je f / (x) = 0 (ovo su nule funkcije). + - - + +

ZADATAK broj 14 Osnovni nivo matematike

Na slici je prikazan grafik funkcije y = f (x), a tačke A, B, C i D su označene na osi Ox. Koristeći graf, svakoj tački dodijelite karakteristike funkcije i njen izvod. ABCD 1) vrijednost funkcije u tački je negativna, a vrijednost izvoda funkcije u tački je pozitivna 2) vrijednost funkcije u tački je pozitivna, a vrijednost izvoda funkcije u tački je negativna 3) vrijednost funkcije u tački je negativna, a vrijednost derivacije funkcije u tački je negativna 4) vrijednost funkcije u tački je pozitivna, a vrijednost derivacija funkcije u tački je pozitivna

№ 1 Na slici je prikazan grafik funkcije y = f (x) i označene tačke A, B, C i D na osi Ox. Koristeći graf, svakoj tački dodijelite karakteristike funkcije i njen izvod. 1) vrijednost funkcije u tački je pozitivna, a vrijednost izvoda funkcije u tački negativna 2) vrijednost funkcije u tački je negativna, a vrijednost derivacije funkcije u tački tačka je negativna 3) vrijednost funkcije u tački je pozitivna, a vrijednost izvoda funkcije u tački je pozitivna 4) vrijednost funkcije u tački je negativna, a vrijednost izvoda funkcije u tački je pozitivan ABCD

Na slici je prikazan grafik funkcije y = f (x). Tačke a, b, c, d i e definiraju intervale na osi Ox. Koristeći graf, dodijelite svakom intervalu karakteristiku funkcije ili njen izvod. A) (a; b) B) (b; c) C) (c; d) D) (d; e) 1) vrijednosti funkcije su pozitivne u svakoj tački intervala 2) vrijednosti ​​izvoda funkcije su negativne u svakoj tački intervala 3) vrijednosti derivacije funkcije su pozitivne u svakoj tački intervala 4) vrijednosti funkcije su negativne u svakoj tački intervala

Na slici je prikazan grafik funkcije y = f (x). Brojevi a, b, c, d i e definiraju intervale na osi Ox. Koristeći graf, dodijelite svakom intervalu karakteristiku funkcije ili njen izvod. A) (a; b) B) (b; c) C) (c; d) D) (d; e) 1) vrijednosti funkcije su pozitivne u svakoj tački intervala 2) vrijednosti ​​funkcije su negativne u svakoj tački intervala 3) vrijednosti izvodnih funkcija su negativne u svakoj tački intervala 4) vrijednosti derivacije funkcije su pozitivne u svakoj tački intervala

Slika prikazuje graf funkcije i tangente povučene na nju u tačkama sa apscisama A, B, C i D. A B C D 1) - 1,5 2) 0,5 3) 2 4) - 0,3

Slika prikazuje graf funkcije i tangente povučene na nju u tačkama sa apscisama A, B, C i D. A B C D 1) 23 2) - 12 3) - 113 4) 123

ZADATAK broj 7 Nivo matematičkog profila

Zadaci za geometrijsko značenje izvoda

1) Na slici je prikazan grafik funkcije y = f (x) i tangente na nju u tački sa apscisom x 0. Pronađite vrijednost izvoda u tački x 0. -2 -0,5 2 0,5 Razmisli! Razmisli! Tačno! Razmisli! x 0 Geometrijsko značenje derivacije: k = tg α Ugao nagiba tangente na osu Ox je tup, pa je k

5 11 8 2) Kontinuirana funkcija y = f (x) postavljena je na interval (-6; 7). Na slici je prikazan njen grafikon. Odrediti broj tačaka u kojima je tangenta na graf funkcije paralelna pravoj liniji y = 6. Provjera y = f (x) y x 3 Razmisli! Razmisli! Razmisli! Tačno! - 6 7 y = 6. Tačka prekida. Izvod NE postoji u ovom trenutku! O -4 3 5 1, 5

Zadaci za određivanje karakteristika funkcije iz grafa njenog izvoda

3) Na slici je prikazan grafik izvoda funkcije y = f / (x), date na intervalu (- 6; 8). Ispitajte funkciju y = f (x) za ekstrem i navedite broj njenih točaka ekstrema. 2 1 4 5 Pogrešno! Nije istina! Tačno! Nije istina! Provjerite (2) f (x) f / (x) -2 + - y = f / (x) 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 4 3 2 1 - 1 -2 -3 -4 -5 yx -5 + min max O

4 -3 -2 -1 1 2 3 4 5 x 5) Na slici je prikazan graf derivacije funkcije specificirane u intervalu [-5; 5]. Ispitajte monotonost funkcije i označite najveću maksimalnu tačku. 3 2 4 5 Razmisli! Razmisli! Tačno! Razmisli! y = f / (x) + + + - - O - f / (x) - + - + - + f (x) -4 -2 0 3 4 Od dvije maksimalne točke, najveći x max = 3 max max y

7) Na slici je prikazan graf derivacije funkcije. Pronađite dužinu rastućeg intervala ove funkcije. Provjerite O -7 -6 -5 -4 -3 -2 -1 7 6 5 4 3 2 1 -1 -2 -3 -4 -5 -6 -7 4 2 3 5 RAZMISLITE! + THINK! PRAVO! THINK! y x 3 y = f / (x)

4 -3 -2 -1 1 2 3 4 5 x 6) Slika prikazuje grafik izvoda funkcije skupa u intervalu [-5; 5]. Ispitati monotonost funkcije y = f (x) i naznačiti broj intervala smanjenja. 3 2 4 1 Razmisli! Razmisli! Tačno! Razmisli! y = f / (x) f (x) -4 -2 0 4 f / (x) - + - + - + + O - - - y

Zadaci za određivanje karakteristika grafskog izvoda funkcije.

Na slici je prikazan graf diferencijabilne funkcije y = f (x). Na apscisi je označeno devet tačaka: x 1, x 2, ..., x 9. Pronađite sve označene tačke u kojima je derivacija funkcije f (x) negativna. U odgovoru navedite broj ovih tačaka.

Na slici je prikazan grafik funkcije y = f (x), definirane na intervalu (a; b). Odrediti broj cjelobrojnih točaka u kojima je derivacija funkcije pozitivna. a) b) Odlučite sami! Rješenje. ako se poveća. Cjelokupna rješenja za: x = -2; x = -1; x = 5; x = 6. Njihov broj je 4. Cjelokupna rješenja za: x = 2; x = 3; x = 4; x = 10; x = 11. Njihov broj je 5. Odgovor: 4. Odgovor: 5.

Problemi za fizičko značenje izvedenice

Odgovor: 3 Odgovor: 14

ZADATAK broj 12 Nivo matematičkog profila

Samostalni rad u paru Zadatak broj 12 Nivo profila

Pregled:

Dodatak 3 pojedinačne kartice br. 12

1. Pronađite maksimalnu tačku funkcije1 Pronađite minimalnu točku funkcije

2. Pronađite maksimalnu točku funkcije2 Pronađite minimalnu točku funkcije

Linnik D. Vovnenko I

1. Pronađite najmanju vrijednost funkcije1. Pronađite najveću vrijednost funkcije na segmentu

na segmentu

Vegelman V.

A.

1. Pronađite maksimalnu tačku funkcije1. Pronađite minimalnu tačku funkcije

2. Pronađite najmanju vrijednost funkcije2. Pronađite najveću vrijednost funkcije na segmentu

Na segmentu

Leontjeva A. Isaenko K.

PRAKSA VAN REVIZIJE 2

Pretvorite grafove funkcija.

Target

Konstruirajte grafove funkcija koristeći različite transformacije, odgovorite na pitanje problema.

Završetak radova

Metodička uputstva

Rad je dizajniran za 10 varijanti, broj varijante se poklapa sa posljednjom znamenkom serijskog broja u listi. Na primjer, 1, 11, 21, 31 ... izvedite 1 opciju, 2,12, 22 ... - 2 opciju, itd.

Rad se sastoji iz dva dijela: prvi dio zadatka 1 - 5, to su zadaci koji se moraju obaviti da bi dobili kredit, ako su ovi zadaci obavljeni sa greškom, moraju se ispraviti i rad se mora predati ponovo na verifikaciju. Drugi dio sadrži zadatke, ispunjavanjem kojih možete dobiti dodatnu ocjenu: glavni dio +2 zadatka - "4", glavni dio +3 zadatka - "5".

Zadatak 1. Grafikon linearne funkcije je prava linija, dvije tačke su dovoljne da se nacrta. (vrijednosti argumenta x uzimamo proizvoljno, a vrijednost funkcije y računamo zamjenom u formulu).

Da biste provjerili da li graf funkcije prolazi kroz navedenu tačku, trebate zamijeniti koordinate tačke umjesto x i y, ako dobijete tačnu jednakost, tada prava linija prolazi kroz navedenu tačku, inače ne .

Zadatak 2, 3, 4. Grafovi navedenih funkcija dobijaju se iz grafova funkcija , koristeći pomak duž x ili y ose.

, prvo crtamo funkciju ili , zatim ga pomaknite za "a" jedinice udesno ili ulijevo (+ a - ulijevo, - i udesno), zatim ga pomaknite za "b" jedinice gore ili dolje (+ b - gore, -b - dolje )

Isto tako i sa ostalim funkcijama:

Zadatak 5 Da nacrtate graf funkcije: , potrebno je da: 1) nacrtate funkciju , 2) ostaviti nepromijenjen dio grafika koji je iznad x ose, 3) preslikati dio grafika koji je ispod x ose.

Zadaci za samostalno rješenje.

Obavezni dio

Zadatak 1. Nacrtajte graf linearne funkcije, odredite da li graf funkcije prolazi kroz navedenu tačku:

Zadatak 2. Nacrtajte graf kvadratne funkcije, odredite skup vrijednosti za ovu funkciju.

Zadatak 3. Izgradite graf funkcije, odredite da li se navedena funkcija povećava ili smanjuje.

Zadatak 4. Napravi graf funkcije, odgovori na pitanje zadatka.

Zadatak 5. Nacrtajte graf funkcije koja sadrži znak modula.

Zadaci za dodatno ocjenjivanje.

Zadatak 6. Nacrtajte graf funkcije date po dijelovima, odredite postoji li tačka prekida za ovu funkciju:

Zadatak 7. Odrediti koliko rješenja ima sistem jednačina, odgovor je opravdati. Izvucite zaključke odgovarajući na pitanja.

Koje ste funkcije zacrtali u ovom radu?

Kako se zove graf linearne funkcije?

Kako se zove graf kvadratne funkcije?

Koje transformacije grafova znate?

Kako se graf parne funkcije nalazi u koordinatnom sistemu? Grafikon neparne funkcije?

Derivat funkcije $ y = f (x) $ u datoj tački $ x_0 $ je granica omjera prirasta funkcije i odgovarajućeg prirasta njenog argumenta, pod uvjetom da potonji teži nuli:

$ f "(x_0) = (lim) ↙ (△ x → 0) (△ f (x_0)) / (△ x) $

Diferencijacija je operacija pronalaženja derivacije.

Derivacijska tablica nekih elementarnih funkcija

Funkcija	Derivat
$ c $	$0$
$ x $	$1$
$ x ^ n $	$ nx ^ (n-1) $
$ (1) / (x) $	$ - (1) / (x ^ 2) $
$ √x $	$ (1) / (2√x) $
$ e ^ x $	$ e ^ x $
$ lnx $	$ (1) / (x) $
$ sinx $	$ cosx $
$ cosx $	$ -sinx $
$ tgx $	$ (1) / (cos ^ 2x) $
$ ctgx $	$ - (1) / (grijeh ^ 2x) $

Osnovna pravila za diferencijaciju

1. Derivat zbira (razlike) jednak je zbiru (razlici) izvoda

$ (f (x) ± g (x)) "= f" (x) ± g "(x) $

Pronađite izvod funkcije $ f (x) = 3x ^ 5-cosx + (1) / (x) $

Izvod zbira (razlike) jednak je zbiru (razlici) izvoda.

$ f "(x) = (3x ^ 5)" - (cos x) "+ ((1) / (x))" = 15x ^ 4 + sinx - (1) / (x ^ 2) $

2. Derivat djela

$ (f (x) g (x)) "= f" (x) g (x) + f (x) g (x) "$

Pronađite Derivat $ f (x) = 4x cosx $

$ f "(x) = (4x)" cosx + 4x (cosx) "= 4 cosx-4x sinx $

3. Derivat količnika

$ ((f (x)) / (g (x))) "= (f" (x) g (x) -f (x) g (x) ") / (g ^ 2 (x)) $

Pronađite izvod $ f (x) = (5x ^ 5) / (e ^ x) $

$ f "(x) = ((5x ^ 5)" e ^ x-5x ^ 5 (e ^ x) ") / ((e ^ x) ^ 2) = (25x ^ 4 e ^ x- 5x ^ 5 e ^ x) / ((e ^ x) ^ 2) $

4. Derivat kompleksne funkcije jednak je umnošku izvoda vanjske funkcije na derivaciju unutrašnje funkcije

$ f (g (x)) "= f" (g (x)) g "(x) $

$ f "(x) = cos" (5x) · (5x) "= - sin (5x) · 5 = -5sin (5x) $

Fizičko značenje izvedenice

Ako se materijalna tačka kreće pravolinijski i njena koordinata se mijenja ovisno o vremenu prema zakonu $ x (t) $, tada je trenutna brzina ove tačke jednaka derivaciji funkcije.

Tačka se kreće duž koordinatne linije prema zakonu $ x (t) = 1,5t ^ 2-3t + 7 $, gdje je $ x (t) $ koordinata u trenutku $ t $. U kom trenutku će brzina tačke biti jednaka 12 $?

1. Brzina je izvod od $ x (t) $, pa nalazimo izvod date funkcije

$ v (t) = x "(t) = 1,5 · 2t -3 = 3t -3 $

2. Da biste pronašli u kojem trenutku je $ t $ brzina bila jednaka $ 12 $, sastavite i riješite jednačinu:

Geometrijsko značenje izvedenice

Podsjetimo da se jednačina prave linije koja nije paralelna sa koordinatnim osa može napisati u obliku $ y = kx + b $, gdje je $ k $ nagib prave linije. Koeficijent $ k $ jednak je tangenti ugla nagiba između prave i pozitivnog smjera $ Ox $ ose.

Derivat funkcije $ f (x) $ u tački $ x_0 $ jednak je nagibu $ k $ tangente na graf u ovoj tački:

Stoga možemo napraviti opštu jednakost:

$ f "(x_0) = k = tgα $

Na slici tangenta na funkciju $ f (x) $ raste, dakle, koeficijent $ k> 0 $. Pošto je $ k> 0 $, onda je $ f "(x_0) = tgα> 0 $. Ugao $ α $ između tangente i pozitivnog pravca $ Ox $ je oštar.

Na slici se tangenta na funkciju $ f (x) $ smanjuje, stoga koeficijent $ k< 0$, следовательно, $f"(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.

Na slici je tangenta funkcije $ f (x) $ paralelna sa $ Ox $ osi, dakle, koeficijent $ k = 0 $, dakle, $ f "(x_0) = tan α = 0 $. tačka $ x_0 $ u kojoj je $ f "(x_0) = 0 $, pozvan ekstremno.

Na slici je prikazan grafik funkcije $ y = f (x) $ i tangenta na ovaj graf, nacrtana u tački sa apscisom $ x_0 $. Pronađite vrijednost derivacije funkcije $ f (x) $ u tački $ x_0 $.

Tangentna linija na graf raste, dakle, $ f "(x_0) = tg α> 0 $

Da biste pronašli $ f "(x_0) $, pronađite tangentu ugla nagiba između tangente i pozitivnog smjera $ Ox $ ose. Da biste to učinili, dodajte tangentu trokutu $ ABC $.

Pronađite tangentu ugla $ BAC $. (Tangens oštrog ugla u pravokutnom trokutu je omjer suprotnog kraka i susjednog kraka.)

$ tg BAC = (BC) / (AC) = (3) / (12) = (1) / (4) = 0,25 $

$ f "(x_0) = tg BAC = 0,25 $

Odgovor: 0,25 dolara

Izvod se također koristi za pronalaženje intervala rastućih i opadajućih funkcija:

Ako je $ f "(x)> 0 $ u intervalu, tada funkcija $ f (x) $ raste u ovom intervalu.

Ako $ f "(x)< 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.

Na slici je prikazan grafik funkcije $ y = f (x) $. Pronađite među tačkama $ x_1, x_2, x_3… x_7 $ one tačke u kojima je derivacija funkcije negativna.

Kao odgovor, zapišite broj bodova.

U zadatku broj 13 USE iz matematike osnovnog nivoa, morat ćete demonstrirati vještine i znanja o jednom od koncepata ponašanja funkcije: izvode u tački ili stope povećanja ili smanjenja. Teorija će biti dodana ovom zadatku malo kasnije, ali to nas ne sprječava da detaljno analiziramo nekoliko tipičnih opcija.

Analiza tipičnih opcija za zadatke br. 14 USE iz matematike osnovnog nivoa

Opcija 14MB1

Na grafikonu je prikazana zavisnost temperature od vremena tokom zagrevanja motora putničkog automobila. Horizontalna os prikazuje vrijeme u minutama koje je proteklo od pokretanja motora; vertikalna os je temperatura motora u stepenima Celzijusa.

Koristeći grafikon, svakom vremenskom intervalu dodijelite karakteristiku procesa zagrijavanja motora u ovom intervalu.

U tabeli ispod svakog slova navedite odgovarajući broj.

Algoritam izvršenja:

1. Odaberite vremenski interval tokom kojeg je temperatura opala.
2. Nanesite ravnalo na 30 °C i odredite vremenski interval tokom kojeg je temperatura bila ispod 30 °C.

Rješenje:

Odaberimo vremenski interval tokom kojeg temperatura pada. Ovo područje je vidljivo golim okom, počinje 8 minuta od trenutka pokretanja motora.

Nanesite ravnalo na 30 °C i odredite vremenski interval u kojem je temperatura bila ispod 30 °C.

Ispod ravnala će se nalaziti dio koji odgovara vremenskom intervalu 0 - 1 min.

Koristeći olovku i ravnalo, pronaći ćemo u kojem vremenskom intervalu je temperatura bila u rasponu od 40 ° C do 80 ° C.

Na grafiku izostavimo okomice iz tačaka koje odgovaraju 40°C i 80°C, a iz dobijenih tačaka izostavićemo okomice na vremensku osu.

Vidimo da ovaj temperaturni interval odgovara vremenskom intervalu od 3 - 6,5 minuta. Odnosno od onih datih u stanju 3 - 6 minuta.

Koristimo metodu eliminacije za odabir odgovora koji nedostaje.

Opcija 14MB2

Rješenje:

Analizirajmo graf funkcije A. Ako funkcija raste, onda je izvod pozitivan i obrnuto. Derivat funkcije je jednak nuli u tačkama ekstrema.

Prvo, funkcija A raste, tj. izvod je pozitivan. Ovo odgovara grafovima izvoda 2 i 3. U tački maksimuma funkcije x = -2, odnosno u ovoj tački izvod mora biti nula. Ovaj uslov je ispunjen grafikonom broj 3.

Prvo, funkcija B se smanjuje, tj. izvod je negativan. Ovo odgovara grafovima izvoda 1 i 4. Maksimalna tačka funkcije je x = -2, odnosno u ovoj tački izvod mora biti jednak nuli. Ovaj uslov je ispunjen grafikonom broj 4.

Prvo, funkcija B raste, tj. izvod je pozitivan. Ovo odgovara grafovima izvoda 2 i 3. Maksimalna tačka funkcije x = 1, odnosno u ovoj tački izvod mora biti jednak nuli. Ovaj uslov je ispunjen grafikonom broj 2.

Metodom eliminacije možemo utvrditi da graf funkcije Γ odgovara grafu derivacije na broju 1.

Odgovor: 3421.

Opcija 14MB3

Algoritam izvršavanja za svaku od funkcija:

1. Odrediti intervale rastućih i opadajućih funkcija.
2. Odredite maksimalnu i minimalnu tačku funkcije.
3. Izvucite zaključke, uskladite predložene rasporede.

Rješenje:

Analizirajmo graf funkcije A.

Ako je funkcija rastuća, onda je derivacija pozitivna i obrnuto. Derivat funkcije je jednak nuli u tačkama ekstrema.

Ekstremna tačka je tačka u kojoj se postiže maksimalna ili minimalna vrednost funkcije.

Prvo, funkcija A raste, tj. izvod je pozitivan. Ovo odgovara grafovima izvoda 3 i 4. U tački maksimuma funkcije x = 0, odnosno u ovoj tački izvod mora biti jednak nuli. Ovaj uslov je ispunjen grafikonom broj 4.

Analizirajmo graf funkcije B.

Prvo, funkcija B se smanjuje, tj. izvod je negativan. Ovo odgovara grafovima izvoda 1 i 2. Minimalna tačka funkcije je x = -1, odnosno u ovoj tački izvod mora biti jednak nuli. Ovaj uslov je ispunjen grafikonom broj 2.

Analizirajmo graf funkcije B.

Prvo, funkcija B se smanjuje, tj. izvod je negativan. Ovo odgovara grafovima izvoda 1 i 2. Minimalna tačka funkcije x = 0, odnosno u ovoj tački izvod mora biti jednak nuli. Ovaj uslov je ispunjen grafikonom broj 1.

Metodom eliminacije možemo utvrditi da graf funkcije Γ odgovara grafu derivacije na broju 3.

Odgovor: 4213.

Opcija 14MB4

Slika prikazuje graf funkcije i tangente povučene na nju u tačkama sa apscisama A, B, C i D.Desna kolona prikazuje vrijednosti izvoda u tačkama A, B, C i D. Koristeći graf, svakoj tački dodijelite vrijednost izvoda funkcije u njoj.

POINTS
A
V
WITH
D

VRIJEDNOSTI DERIVATA
1) –4
2) 3
3) 2/3
4) -1/2

Prisjetimo se šta derivacija znači, odnosno njegovu vrijednost u tački - vrijednost funkcije derivacije u tački jednaka je tangentu nagiba (koeficijentu) tangente.

U odgovorima imamo dvije pozitivne i dvije negativne opcije. Kao što se sjećamo, ako je koeficijent prave linije (grafik y = kx + b) pozitivan, tada se prava povećava, ako je negativna, tada se prava smanjuje.

Imamo dvije rastuće prave - u tačkama A i D. Prisjetimo se sada šta znači vrijednost koeficijenta k?

Koeficijent k pokazuje koliko brzo se funkcija povećava ili smanjuje (u stvari, sam koeficijent k je izvod funkcije y = kx + b).

Dakle, k = 2/3 odgovara ravnijoj liniji - D, a k = 3 - A.

Slično, u slučaju negativnih vrijednosti: tačka B odgovara strmijoj pravoj liniji sa k = - 4, a tački C - -1/2.

Opcija 14MB5

Na slici, tačke pokazuju mjesečnu prodaju grijača u prodavnici kućanskih aparata. Mjeseci su prikazani horizontalno, a broj prodatih grijača vertikalno. Radi jasnoće, tačke su povezane linijom.

Koristeći sliku, uparite svaki od navedenih vremenskih perioda sa prodajnom karakteristikom grijača.

Algoritam izvršenja

Analiziramo dijelove grafikona koji odgovaraju različitim godišnjim dobima. Formuliramo situacije prikazane na grafikonu. Pronalazimo najprikladnije opcije odgovora za njih.

Rješenje:

Zimi je broj prodaje prelazio 120 kom/mjesečno i stalno se povećavao. Ova situacija odgovara odgovoru broj 3. One. dobijamo: A – 3.

U proljeće je prodaja postepeno pala sa 120 grijača mjesečno na 50. Opcija 2 je najbliža ovoj formulaciji. Imamo: B – 2.

Ljeti se broj rasprodaja nije mijenjao i bio je minimalan. Drugi dio ove formulacije se ne odražava u odgovorima, a za prvi je pogodan samo #4. Stoga imamo: U 4.

U jesen je prodaja rasla, ali njihov broj ni u jednom od mjeseci nije premašio 100 jedinica. Ova situacija je opisana u opciji broj 1. Dobijamo: G – 1.

Opcija 14MB6

Grafikon prikazuje zavisnost brzine redovnog autobusa od vremena. Na vertikalnoj osi brzina autobusa je označena u km/h, na horizontalnoj - vrijeme u minutama od početka kretanja autobusa.

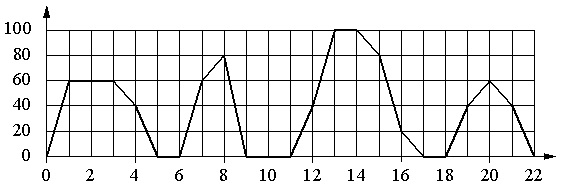
Koristeći graf, dodijelite svakom vremenskom intervalu karakteristiku kretanja sabirnice u ovom intervalu.

Algoritam izvršenja

1. Odredite cijenu podjele na horizontalnoj i vertikalnoj skali.
2. Analiziramo redom predložene izjave 1–4 iz desne kolone („Karakteristike“). Upoređujemo ih sa vremenskim intervalima iz lijevog stupca tabele, nalazimo parove „slovo-broj“ za odgovor.

Rješenje:

Podjela na horizontalnoj skali je 1 s, a na vertikalnoj 20 km/h.

1. Kada se autobus zaustavi, njegova brzina je 0. Autobus je imao nultu brzinu 2 minute zaredom samo od 9. do 11. minute. Ovo vrijeme je u intervalu od 8-12 minuta. Dakle, imamo par za odgovor: B – 1.
2. Autobus je imao brzinu od 20 km/h i više u nekoliko vremenskih intervala. Štaviše, opcija A ovdje nije prikladna, jer je npr. u 7. minuti brzina bila 60 km/h, opcija B - jer je već primijenjena, opcija D - jer je na početku i na kraju intervala autobus imao nultu brzinu... U ovom slučaju je prikladna opcija B (12–16 min); u tom intervalu autobus počinje da se kreće brzinom od 40 km/h, zatim ubrzava do 100 km/m i zatim postepeno smanjuje brzinu na 20 km/h. Dakle, imamo: U 2.
3. Ovdje je postavljeno ograničenje brzine. Istovremeno, ne razmatramo opcije B i C. Preostali intervali A i D su prikladni. Stoga bi bilo ispravno prvo razmotriti 4. opciju, a zatim se ponovo vratiti na 3. opciju.
4. Od dva preostala intervala, samo 4-8 minuta je pogodno za karakteristiku br. 4, jer je u tom intervalu (u 6. minuti) došlo do zaustavljanja. Nije bilo zaustavljanja u intervalu od 18-22 minuta. Dobijamo: A – 4... Otuda slijedi da je za karakteristiku br. 3 potrebno uzeti interval G, tj. ispada par G – 3.

Opcija 14MB7

Tačkasta cifra pokazuje povećanje kineske populacije od 2004. do 2013. godine. Horizontalno označava godinu, vertikalno - rast stanovništva u procentima (povećanje stanovništva u odnosu na prošlu godinu). Radi jasnoće, tačke su povezane linijom.

Koristeći sliku, uparite svaki od navedenih vremenskih perioda sa karakteristikama rasta stanovništva Kine tokom ovog perioda..

Algoritam izvršenja

1. Odredite cijenu podjele vertikalne skale slike. Nalazi se kao razlika između para susednih vrednosti na skali, podeljenih sa 2 (pošto postoje 2 podele između dve susedne vrednosti).
2. Analiziramo sekvencijalno karakteristike 1–4 date u uslovu (lijeva kolona tabele). Svaki od njih upoređujemo sa određenim vremenskim periodom (desna kolona tabele).

Rješenje:

Podjela vertikalne skale je 0,01%.

1. Pad rasta nastavio se kontinuirano od 2004. do 2010. godine. U periodu 2010–2011. rast je bio stabilno minimalan, a od 2012. je počeo da raste. One. rast je zaustavljen 2010. Ova godina je u periodu 2009–2011. Shodno tome, imamo: U 1.
2. „Najstrmiju“ liniju pada grafikona na slici treba smatrati najvećim padom rasta. Pada na period 2006-2007. i iznosi 0,04% godišnje (0,59-0,56 = 0,04% u 2006. i 0,56-0,52 = 0,04% u 2007.). Odavde dobijamo: A – 2.
3. Rast naznačen u karakteristici broj 3 započeo je 2007. godine, nastavio se 2008. godine i završio 2009. godine. Ovo odgovara vremenskom periodu B, tj. imamo: B – 3.
4. Rast stanovništva počeo je rasti nakon 2011. godine, tj. u 2012–2013 Dakle, dobijamo: G-4.

Opcija 14MB8

Slika prikazuje graf funkcije i tangente povučene na nju u tačkama sa apscisama A, B, C i D.

Desni stupac prikazuje vrijednosti izvoda funkcije u tačkama A, B, C i D. Koristeći graf, svakoj tački dodijelite vrijednost derivacije funkcije u njoj.

Algoritam izvršenja

1. Razmotrimo par tangenta koji imaju oštar ugao sa pozitivnim smjerom ose apscise. Uspoređujemo ih, pronalazimo podudaranje među parom odgovarajućih vrijednosti derivata.
2. Zamislite par tangenti koje formiraju tupi ugao sa pozitivnim smjerom ose apscise. Uspoređujemo ih u apsolutnoj vrijednosti, utvrđujemo njihovu korespondenciju sa vrijednostima derivata između dva preostala u desnom stupcu.

Rješenje:

Oštar ugao s pozitivnim smjerom ose apscise formiraju derivacije u tački B i tački C. Ovi derivati ​​imaju pozitivne vrijednosti. Dakle, ovdje treba birati između vrijednosti br. 1 i 3. Primjenjujući pravilo da ako je ugao manji od 45 0, onda je derivacija manja od 1, a ako je više, onda više od 1, zaključujemo: u tački B derivacija u modulu je veća od 1, u tački C - manja od 1. To znači da možete sastaviti parove za odgovor: U 3 i S – 1.

Derivati ​​u tački A i tački D formiraju tup ugao sa pozitivnim smerom apscise. I ovdje primjenjujemo isto pravilo, parafrazirajući ga malo: što je tangenta u tački više "pritisnuta" na liniju apscise (u njenom negativnom smjeru), to je veća u apsolutnoj vrijednosti. Tada dobijamo: izvod u tački A je manji po apsolutnoj vrednosti od izvoda u tački D. Dakle, imamo parove za odgovor: A – 2 i D – 4.

Opcija 14MB9

Na slici, tačke pokazuju prosječnu dnevnu temperaturu zraka u Moskvi u januaru 2011. godine. Horizontalno označava dan u mjesecu, vertikalno - temperaturu u stepenima Celzijusa. Radi jasnoće, tačke su povezane linijom.

Koristeći sliku, uparite svaki od naznačenih vremenskih perioda sa karakteristikom promjene temperature.

Algoritam izvršenja

Analiziramo sekvencijalno karakteristike 1-4 (desni stupac), koristeći grafikon na slici. Svaku od njih stavljamo u korespondenciju sa određenim vremenskim periodom (lijeva kolona).

Rješenje:

1. Porast temperature uočen je tek na kraju perioda 22–28. januara. Ovdje je 27. i 28. porasla za 1 odnosno 2 stepena. Na kraju perioda 1–7. januara temperatura je bila stabilna (–10 stepeni), krajem 8–14. i 15–21. januara opadala (od –1 do –2 i od –11 do – 12 stepeni, respektivno). Dakle, dobijamo: G – 1.
2. Pošto svaki vremenski period obuhvata 7 dana, temperaturu je potrebno analizirati počevši od 4. dana svakog perioda. Temperatura je ostala nepromijenjena 3-4 dana samo od 4. do 7. januara. Dakle, dobijamo odgovor: A – 2.
3. Mjesečna minimalna temperatura zabilježena je 17. januara. Ovaj broj je u periodu od 15. do 21. januara. Odavde imamo par: U 3.
4. Temperaturni maksimum pao je 10. januara i iznosio je +1 stepen. Ovaj datum pada između 8. i 14. januara. Dakle, imamo: B – 4.

Opcija 14MB10

Algoritam izvršenja

1. Vrijednost funkcije u tački je pozitivna ako se ta tačka nalazi iznad ose Ox.
2. Izvod u tački je veći od nule ako tangenta na ovu tačku formira oštar ugao s pozitivnim smjerom ose Ox.

Rješenje:

Tačka A. Nalazi se ispod ose Ox, što znači da je vrijednost funkcije u njoj negativna. Ako u njemu nacrtate tangentu, tada će ugao između nje i pozitivnog smjera Ox biti oko 90 0, tj. formira oštar ugao. Dakle, u ovom slučaju je prikladna karakteristika broj 3. One. imamo: A – 3.

Tačka B. Nalazi se iznad ose Ox, tj. tačka ima pozitivnu vrijednost funkcije. Tangentna linija u ovoj tački bit će prilično blizu osi apscise, formirajući tupi ugao (nešto manji od 180 0) sa svojim pozitivnim smjerom. Prema tome, izvod je u ovom trenutku negativan. Dakle, ovdje je prikladna karakteristika 1. Dobijamo odgovor: U 1.

Tačka C. Tačka se nalazi ispod ose Ox, tangenta u njoj formira veliki tupi ugao sa pozitivnim smjerom ose apscise. One. u tački C, vrijednost i funkcije i derivacije je negativna, što odgovara karakteristici br. 2. odgovor: C – 2.

Tačka D. Tačka je iznad ose Ox, a tangenta u njoj formira oštar ugao sa pozitivnim smjerom ose. Ovo sugerira da su i vrijednost funkcije i vrijednost derivacije ovdje veće od nule. odgovor: D – 4.

Opcija 14MB11

Na slici, tačke pokazuju mjesečnu prodaju frižidera u prodavnici kućnih aparata. Mjeseci su prikazani horizontalno, a broj prodatih frižidera vertikalno. Radi jasnoće, tačke su povezane linijom.

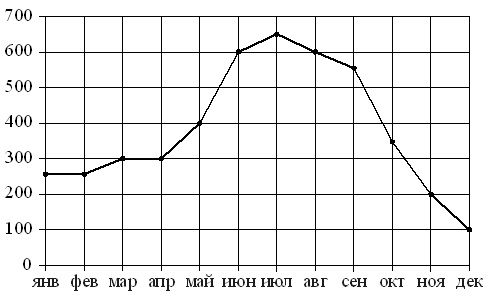
Koristeći sliku, uparite svaki od navedenih vremenskih perioda sa prodajnom karakteristikom frižidera..