त्रिकोणमिति में अंतराल में जड़ें कैसे खोजें I खंड से संबंधित समीकरण के मूल ज्ञात करना। जड़ों का चयन करने के विभिन्न तरीके

समस्या संख्या 1

तर्क सरल है: हम पहले की तरह कार्य करेंगे, इस तथ्य के बावजूद कि अब त्रिकोणमितीय कार्यों में एक अधिक जटिल तर्क है!

अगर हमें फॉर्म के समीकरण को हल करना था:

तब हम निम्नलिखित उत्तर लिखेंगे:

या (चूंकि)

लेकिन अब हमारी भूमिका में निम्नलिखित अभिव्यक्ति है:

तब आप लिख सकते हैं:

आपके साथ हमारा लक्ष्य बिना किसी "अशुद्धता" के, बाएं स्टैंड को सरल बनाना है!

आइए धीरे-धीरे इनसे छुटकारा पाएं!

सबसे पहले, हम हर को यहां से हटाते हैं: इसके लिए हम अपनी समानता को इससे गुणा करते हैं:

अब इसके दोनों भागों को इसमें बाँट कर इससे छुटकारा पाते हैं:

आइए अब आठ से छुटकारा पाएं:

परिणामी अभिव्यक्ति को समाधान की 2 श्रृंखला के रूप में लिखा जा सकता है (एक द्विघात समीकरण के साथ सादृश्य द्वारा, जहां हम या तो विवेचक को जोड़ते या घटाते हैं)

हमें सबसे बड़ी नकारात्मक जड़ खोजने की जरूरत है! यह स्पष्ट है कि इसे सुलझाना आवश्यक है।

पहले पहली श्रृंखला पर विचार करें:

यह स्पष्ट है कि यदि हम लेते हैं, तो परिणामस्वरूप हमें सकारात्मक संख्याएँ मिलेंगी, और वे हमारे लिए रुचिकर नहीं हैं।

इसलिए आपको इसे नेगेटिव लेने की जरूरत है। होने देना।

जब जड़ पहले से ही है:

और हमें सबसे बड़ा नकारात्मक खोजने की जरूरत है !! इसका मतलब है कि अब नकारात्मक दिशा में जाने का कोई मतलब नहीं है। और इस श्रंखला के लिए सबसे बड़ा ऋणात्मक मूल होगा।

अब दूसरी श्रृंखला पर नजर डालते हैं:

और फिर से हम स्थानापन्न करते हैं:, फिर:

रुचि नहीं!

तब और बढ़ने का कोई मतलब नहीं है! हम कम करेंगे! चलो, फिर:

फिट बैठता है!

होने देना। फिर

तब - सबसे बड़ी नकारात्मक जड़!

उत्तर:

समस्या संख्या 2

फिर से हम जटिल कोसाइन तर्क की परवाह किए बिना हल करते हैं:

अब हम फिर से बाईं ओर व्यक्त करते हैं:

हम दोनों पक्षों को से गुणा करते हैं

हम दोनों पक्षों को विभाजित करते हैं

जो कुछ बचा है, उसे माइनस से प्लस में बदलते हुए, इसे दाईं ओर ले जाना है।

हमारे पास फिर से जड़ों की 2 श्रृंखलाएं हैं, एक के साथ और दूसरी के साथ।

हमें सबसे बड़ा ऋणात्मक मूल खोजने की आवश्यकता है। पहली श्रृंखला पर विचार करें:

यह स्पष्ट है कि हमें पहला ऋणात्मक मूल प्राप्त होगा, यह बराबर होगा और 1 श्रृंखला में सबसे बड़ा ऋणात्मक मूल होगा।

दूसरी श्रृंखला के लिए

पहला ऋणात्मक मूल भी पर प्राप्त होगा और इसके बराबर होगा। चूँकि, तब समीकरण का सबसे बड़ा ऋणात्मक मूल है।

उत्तर: .

समस्या संख्या 3

जटिल स्पर्शरेखा तर्क की परवाह किए बिना हल करें।

ऐसा लगता है कि कुछ भी जटिल नहीं है, है ना?

पहले की तरह, हम बाईं ओर व्यक्त करते हैं:

खैर, यह बहुत अच्छा है, यहाँ जड़ों की केवल एक श्रृंखला है! सबसे बड़ा ऋणात्मक फिर से खोजें।

यह स्पष्ट है कि अगर हम डालते हैं तो यह निकलता है। और यह जड़ बराबर है।

उत्तर:

अब निम्नलिखित समस्याओं को स्वयं हल करने का प्रयास करें।

एक स्वतंत्र समाधान के लिए गृहकार्य या 3 कार्य।

निर्णय-शि-ते समीकरण।
निर्णय-शि-ते समीकरण।
ओट-वे-वो ना-पी-शि-ते में, सबसे छोटा पो-ली-टेल-रूट।
निर्णय-शि-ते समीकरण।
ओट-वे-वो ना-पी-शि-ते में, सबसे छोटा पो-ली-टेल-रूट।

तैयार? जाँच हो रही है। मैं पूरे समाधान एल्गोरिथ्म का विस्तार से वर्णन नहीं करूंगा, मुझे ऐसा लगता है कि ऊपर पहले ही इस पर पर्याप्त ध्यान दिया जा चुका है।

अच्छा, क्या सब कुछ सही है? ओह, उन गंदे साइनस, उनके साथ हमेशा कुछ परेशानी होती है!

खैर, अब आप सबसे सरल त्रिकोणमितीय समीकरणों को हल कर सकते हैं!

समाधान और उत्तर जांचें:

समस्या संख्या 1

आइए व्यक्त करें

सबसे छोटा धनात्मक मूल प्राप्त होता है, यदि हम तब से, तब

उत्तर:

समस्या संख्या 2

सबसे छोटी धनात्मक जड़ कब प्राप्त होती है।

बराबर होगा।

उत्तर: .

समस्या संख्या 3

जब हम प्राप्त करते हैं, जब हम प्राप्त करते हैं।

उत्तर: .

यह ज्ञान आपको परीक्षा में आने वाली कई समस्याओं को हल करने में मदद करेगा।

यदि आप "5" के ग्रेड के लिए आवेदन कर रहे हैं, तो आपको बस के लिए लेख पढ़ने की आवश्यकता है मध्य स्तर,जो अधिक जटिल त्रिकोणमितीय समीकरणों (कार्य C1) को हल करने के लिए समर्पित होगा।

औसत स्तर

इस लेख में मैं वर्णन करूंगा अधिक जटिल प्रकार के त्रिकोणमितीय समीकरणों को हल करनाऔर उनकी जड़ों का चयन कैसे करें। यहां मैं निम्नलिखित विषयों पर निर्माण करूंगा:

प्रवेश स्तर के लिए त्रिकोणमितीय समीकरण (ऊपर देखें)।

अधिक जटिल त्रिकोणमितीय समीकरण अधिक जटिल समस्याओं का आधार होते हैं। उनमें, समीकरण को सामान्य रूप में ही हल करना और एक निश्चित निर्दिष्ट अंतराल से संबंधित इस समीकरण की जड़ों को खोजने के लिए दोनों की आवश्यकता होती है।

त्रिकोणमितीय समीकरणों को हल करना दो उप-कार्यों में आता है:

समीकरण समाधान
जड़ों का चयन

यह ध्यान दिया जाना चाहिए कि उत्तरार्द्ध की हमेशा आवश्यकता नहीं होती है, लेकिन फिर भी अधिकांश उदाहरणों में चयन की आवश्यकता होती है। और अगर इसकी आवश्यकता नहीं है, तो आप सहानुभूति रख सकते हैं - इसका मतलब है कि समीकरण अपने आप में काफी जटिल है।

C1 कार्यों को पार्स करने में मेरा अनुभव दर्शाता है कि वे आमतौर पर इन श्रेणियों में विभाजित होते हैं।

बढ़ी हुई जटिलता के कार्यों की चार श्रेणियां (पूर्व में C1)

समीकरण जो गुणनखंड को कम करते हैं।
फॉर्म को कम करने वाले समीकरण।
चर परिवर्तन द्वारा हल किए गए समीकरण।
तर्कहीनता या हर के कारण जड़ों के अतिरिक्त चयन की आवश्यकता वाले समीकरण।

इसे सीधे शब्दों में कहें: यदि आप सामने आते हैं पहले तीन प्रकार के समीकरणों में से एकतो अपने आप को भाग्यशाली समझो। उनके लिए, एक नियम के रूप में, आपको अतिरिक्त रूप से एक निश्चित अंतराल से संबंधित जड़ों को लेने की आवश्यकता होती है।

यदि आप टाइप 4 के समीकरण को देखते हैं, तो आप कम भाग्यशाली हैं: आपको इसके साथ थोड़ी देर और अधिक बारीकी से छेड़छाड़ करने की आवश्यकता है, लेकिन अक्सर इसमें जड़ों के अतिरिक्त चयन की आवश्यकता नहीं होती है। फिर भी, मैं अगले लेख में इस प्रकार के समीकरणों का विश्लेषण करूंगा, और यह पहले तीन प्रकार के समीकरणों को हल करने के लिए समर्पित होगा।

फैक्टरिंग समीकरण

इस प्रकार के समीकरणों को हल करने के लिए याद रखने वाली सबसे महत्वपूर्ण बात है

जैसा कि अभ्यास से पता चलता है, एक नियम के रूप में, यह ज्ञान पर्याप्त है। आइए कुछ उदाहरण देखें:

उदाहरण 1. न्यूनीकरण सूत्र और द्विकोण ज्या का उपयोग करके गुणनखंडन में कमी करने वाला समीकरण

रेस-शि-ते समीकरण
Nay-di-te इस समीकरण के सभी मूल

यहाँ, जैसा कि मैंने वादा किया था, कास्टिंग सूत्र काम करते हैं:

तब मेरा समीकरण इस तरह दिखेगा:

तब मेरा समीकरण निम्नलिखित रूप लेगा:

एक अदूरदर्शी छात्र कह सकता है: और अब मैं दोनों भागों को छोटा कर दूंगा, सरलतम समीकरण प्राप्त करूंगा और जीवन का आनंद लूंगा! और यह कड़वा गलत होगा!

याद रखें: त्रिकोणमितीय समीकरण के दोनों हिस्सों को एक अज्ञात वाले फ़ंक्शन द्वारा कभी भी कम न करें! तो आप जड़ें खो देते हैं!

तो तुम क्या करते हो? हां, सब कुछ सरल है, सब कुछ एक दिशा में ले जाएं और सामान्य कारक निकालें:

खैर, हम इसे कारकों में शामिल करते हैं, हुर्रे! अब हम तय करते हैं:

पहले समीकरण की जड़ें हैं:

और दूसरा:

यह समस्या का पहला भाग पूरा करता है। अब हमें जड़ों का चयन करने की आवश्यकता है:

अंतराल इस प्रकार है:

या इसे इस प्रकार भी लिखा जा सकता है:

खैर, आइए जड़ें लें:

सबसे पहले, आइए पहली श्रृंखला के साथ काम करें (और यह आसान है, हम क्या कह सकते हैं!)

चूंकि हमारा अंतराल पूरी तरह से नकारात्मक है, इसलिए गैर-नकारात्मक को लेने की कोई आवश्यकता नहीं है, वैसे ही वे गैर-नकारात्मक जड़ें देंगे।

चलो, फिर - थोड़ा बहुत, फिट नहीं है।

चलो, फिर - फिर नहीं मारा।

एक और प्रयास - फिर - है, हिट! पहली जड़ मिली!

मैं फिर से गोली मारता हूं: फिर - मैंने इसे फिर से मारा!

खैर, एक बार और :: - यह पहले से ही एक उड़ान है।

तो पहली श्रृंखला से 2 जड़ें अंतराल से संबंधित हैं:।

हम दूसरी श्रृंखला के साथ काम कर रहे हैं (हम निर्माण कर रहे हैं नियम के अनुसार एक हद तक):

अंडरशूट!

फिर से अंडरशूट!

समझ लिया!

उड़ान!

इस प्रकार, निम्नलिखित जड़ें मेरी अवधि से संबंधित हैं:

इस एल्गोरिथम द्वारा हम अन्य सभी उदाहरणों को हल करेंगे। आइए एक और उदाहरण के साथ मिलकर अभ्यास करें।

उदाहरण 2. एक समीकरण जो अपचयन सूत्रों का उपयोग करके गुणनखंडन को घटाता है

प्रश्न हल करें

समाधान:

फिर से कुख्यात कास्टिंग सूत्र:

दोबारा, कम करने की कोशिश मत करो!

पहले समीकरण की जड़ें हैं:

और दूसरा:

अब फिर से जड़ों की तलाश करें।

मैं दूसरी श्रृंखला के साथ शुरू करूँगा, मैं इसके बारे में पिछले उदाहरण से पहले से ही सब कुछ जानता हूँ! देखें और सुनिश्चित करें कि अंतराल से संबंधित जड़ें इस प्रकार हैं:

अब पहला एपिसोड और यह आसान है:

अगर - फिट

अगर - भी अच्छा है

अगर - पहले से ही एक उड़ान।

तब जड़ें इस प्रकार होंगी:

स्वतंत्र काम। 3 समीकरण।

ठीक है, क्या तकनीक आपके लिए स्पष्ट है? त्रिकोणमितीय समीकरणों को हल करना अब इतना कठिन नहीं लगता? फिर निम्नलिखित समस्याओं को जल्दी से स्वयं हल करें, और फिर आप और मैं अन्य उदाहरणों को हल करेंगे:

प्रश्न हल करें
Nay-di-वे इस समीकरण के सभी मूल हैं, जो अंतराल से जुड़े हैं।
रेस-शि-ते समीकरण
समीकरण की जड़ों को इंगित करें
रेस-शि-ते समीकरण
Nay-di-वे सभी इस समीकरण की जड़ें हैं-गैर-एनआई, संलग्न-ओवर-ले-झा-शि-प्रो-मी-झुत-कु।

समीकरण 1.

और फिर से कास्टिंग सूत्र:

जड़ों की पहली श्रृंखला:

जड़ों की दूसरी श्रृंखला:

अंतराल के लिए चयन शुरू

उत्तर: , ।

समीकरण 2. स्वतंत्र कार्य की जाँच करना।

कारकों में काफी मुश्किल समूह (मैं डबल कोण साइन फॉर्मूला का उपयोग करूंगा):

फिर या

यह एक सामान्य समाधान है। अब हमें जड़ों का चयन करने की आवश्यकता है। परेशानी यह है कि हम उस कोण का सटीक मान नहीं बता सकते, जिसकी कोज्या एक चौथाई के बराबर होती है। इसलिए, मैं सिर्फ आर्ककोसाइन से छुटकारा नहीं पा सकता - यह बहुत शर्म की बात है!

मैं क्या कर सकता हूं यह पता लगाना है कि फिर कैसे।

आइए एक तालिका बनाएं: अंतराल:

खैर, दर्दनाक खोजों के माध्यम से, हम निराशाजनक निष्कर्ष पर पहुंचे कि हमारे समीकरण में संकेतित अंतराल पर एक जड़ है: \ डिस्प्लेस्टाइल आर्ककोस \ फ़्रेक (1) (4) -5 \ pi

समीकरण 3. स्वतंत्र कार्य की जाँच करना।

एक भयावह समीकरण। हालाँकि, इसे डबल एंगल साइन फॉर्मूला लागू करके काफी सरलता से हल किया जा सकता है:

2 से कम करें:

आइए पहले पद को दूसरे के साथ और तीसरे को चौथे के साथ समूहित करें और सामान्य कारकों को निकालें:

यह स्पष्ट है कि पहले समीकरण का कोई मूल नहीं है, और अब दूसरे पर विचार करें:

सामान्य तौर पर, मैं इस तरह के समीकरणों के समाधान पर थोड़ी देर बाद ध्यान केंद्रित करने वाला था, लेकिन जब से यह निकला, तब करने के लिए कुछ नहीं है, इसे हल करना आवश्यक है ...

फॉर्म के समीकरण:

यह समीकरण दोनों भागों को विभाजित करके हल किया जाता है:

इस प्रकार, हमारे समीकरण में जड़ों की एक श्रृंखला है:

उनमें से उन लोगों को ढूंढना आवश्यक है जो अंतराल से संबंधित हैं:।

चलिए फिर से टेबल बनाते हैं, जैसा कि मैंने पहले किया था:

उत्तर: ।

समीकरण जो फ़ॉर्म को कम करते हैं:

खैर, अब समीकरणों के दूसरे बैच पर आगे बढ़ने का समय है, खासकर जब से मैंने पहले ही यह बताया है कि एक नए प्रकार के त्रिकोणमितीय समीकरणों के समाधान में क्या शामिल है। लेकिन यह दोहराना अतिश्योक्तिपूर्ण नहीं होगा कि फॉर्म का एक समीकरण

इसे कोज्या द्वारा दोनों भागों को विभाजित करके हल किया जाता है:

रेस-शि-ते समीकरण
समीकरण-नहीं-निया, जब-ओवर-लेट-से-काटने की जड़ों को इंगित करें।
रेस-शि-ते समीकरण
समीकरण-न-निया की जड़ों को इंगित करें, जब-ओवर-ले-झा-शि-प्रो-मी-झुट-कु।

उदाहरण 1।

पहला बहुत सरल है। दाईं ओर जाएँ और दोहरा कोण कोसाइन सूत्र लागू करें:

आह! फॉर्म का समीकरण:। मैं दोनों भागों को में बाँटता हूँ

हम जड़ों को छानते हैं:

गैप:

उत्तर:

उदाहरण 2।

सब कुछ बहुत मामूली है: आइए दाईं ओर कोष्ठक का विस्तार करें:

मूल त्रिकोणमितीय पहचान:

डबल कोण साइन:

हम अंत में प्राप्त करते हैं:

रूट ड्रॉपआउट: गैप।

उत्तर: ।

ठीक है, आपको तकनीक कैसी लगी, क्या यह बहुत जटिल नहीं है? मुझे आशा नहीं है। हम तुरंत आरक्षण कर सकते हैं: अपने शुद्ध रूप में, समीकरण, जो तुरंत स्पर्शरेखा के लिए समीकरण को कम कर देते हैं, काफी दुर्लभ हैं। आमतौर पर, यह संक्रमण (कोसाइन द्वारा विभाजन) एक अधिक जटिल समस्या का केवल एक हिस्सा है। अभ्यास करने के लिए यहां एक उदाहरण दिया गया है:

रेस-शि-ते समीकरण
Nay-di-वे सभी इस समीकरण की जड़ें हैं-नहीं-निया, संलग्न-ओवर-ले-ज़ा-शि-कु।

चलो जांचते हैं:

समीकरण तुरंत हल हो जाता है, यह दोनों भागों को विभाजित करने के लिए पर्याप्त है:

रूट ड्रॉपआउट:

उत्तर: ।

एक तरह से या किसी अन्य, हमें अभी तक उस तरह के समीकरणों से मिलना बाकी है जिनका हमने अभी विश्लेषण किया है। हालाँकि, हमारे लिए इसे समाप्त करना जल्दबाजी होगी: समीकरणों की एक और "परत" है जिसका हमने विश्लेषण नहीं किया है। इसलिए:

एक चर बदलकर त्रिकोणमितीय समीकरणों को हल करना

यहां सब कुछ पारदर्शी है: हम समीकरण को करीब से देखते हैं, जितना संभव हो इसे सरल बनाते हैं, एक प्रतिस्थापन करते हैं, हल करते हैं, एक रिवर्स प्रतिस्थापन करते हैं! शब्दों में, सब कुछ बहुत आसान है। आइए कार्रवाई में देखें:

उदाहरण।

प्रश्न हल करें:।
Nay-di-वे सभी इस समीकरण की जड़ें हैं-नहीं-निया, संलग्न-ओवर-ले-ज़ा-शि-कु।

खैर, यहाँ प्रतिस्थापन ही हमारे हाथ में होना चाहता है!

तब हमारा समीकरण इसमें बदल जाएगा:

पहले समीकरण की जड़ें हैं:

और दूसरा ये है:

अब हम अंतराल से संबंधित मूल पाएंगे

उत्तर: ।

आइए एक साथ थोड़ा और जटिल उदाहरण देखें:

रेस-शि-ते समीकरण
दिए गए समीकरण-नॉन-निय, व्हेन-ओवर-ले-ज़ा-शि-एन-ए-झुट-कु की जड़ों को इंगित करें।

यहां प्रतिस्थापन तुरंत दिखाई नहीं देता है, इसके अलावा, यह बहुत स्पष्ट नहीं है। आइए पहले सोचें: हम क्या कर सकते हैं?

उदाहरण के लिए, हम कल्पना कर सकते हैं

और उस समय पर ही

तब मेरा समीकरण रूप लेगा:

अब ध्यान दें, ध्यान दें:

आइए समीकरण के दोनों पक्षों को इस प्रकार विभाजित करें:

अचानक आपको और मुझे द्विघात समीकरण मिल गया! आइए एक प्रतिस्थापन करें, फिर हमें मिलता है:

समीकरण की निम्नलिखित जड़ें हैं:

जड़ों की खराब दूसरी श्रृंखला, लेकिन इसकी मदद नहीं की जा सकती! हम अंतराल में जड़ों का चयन करते हैं।

हमें उस पर भी विचार करने की आवश्यकता है

तब से और तब से

उत्तर:

समेकित करने के लिए, इससे पहले कि आप स्वयं समस्याओं का समाधान करें, यहां आपके लिए एक और अभ्यास है:

रेस-शि-ते समीकरण
Nay-di-वे सभी इस समीकरण की जड़ें हैं-गैर-एनआई, संलग्न-ओवर-ले-झा-शि-प्रो-मी-झुत-कु।

यहां आपको अपनी आंखें खुली रखने की जरूरत है: अब हमारे पास शून्य हो सकते हैं! इसलिए, आपको जड़ों के प्रति विशेष रूप से चौकस रहने की आवश्यकता है!

सबसे पहले, मुझे समीकरण को बदलने की जरूरत है ताकि मैं एक उपयुक्त प्रतिस्थापन कर सकूं। मैं साइन और कोसाइन के संदर्भ में स्पर्शरेखा को फिर से लिखने की तुलना में अभी कुछ भी बेहतर नहीं सोच सकता:

अब मैं मूल त्रिकोणमितीय पहचान द्वारा कोसाइन से साइन में जाऊंगा:

और अंत में, मैं सब कुछ एक सामान्य हर में लाऊंगा:

अब मैं समीकरण पर जा सकता हूं:

लेकिन पर (अर्थात, पर)।

सब कुछ अब प्रतिस्थापन के लिए तैयार है:

तो कोई

हालाँकि, कृपया ध्यान दें कि यदि, तो उसी समय!

इससे कौन पीड़ित है? स्पर्शरेखा के साथ परेशानी, यह अपरिभाषित है जब कोसाइन शून्य है (शून्य से विभाजन)।

इस प्रकार, समीकरण की जड़ें इस प्रकार हैं:

अब हम अंतराल में जड़ों को छानते हैं:


	- फिट बैठता है
	- पाशविक बल

इस प्रकार, हमारे समीकरण का अंतराल में एक ही मूल है, और यह बराबर है।

आप देखते हैं: हर की उपस्थिति (साथ ही स्पर्शरेखा, जड़ों के साथ कुछ कठिनाइयों की ओर ले जाती है! यहां आपको अधिक सावधान रहने की आवश्यकता है!)।

ठीक है, आपने और मैंने त्रिकोणमितीय समीकरणों का विश्लेषण लगभग समाप्त कर लिया है, दो समस्याओं को स्वतंत्र रूप से हल करने के लिए बहुत कम बचा है। वे यहाँ हैं।

प्रश्न हल करें
Nay-di-वे सभी इस समीकरण की जड़ें हैं-नहीं-निया, संलग्न-ओवर-ले-ज़ा-शि-कु।
रेस-शि-ते समीकरण
कट से जुड़े इस समीकरण की जड़ों को इंगित करें।

निर्णय लिया? बहुत मुश्किल नहीं है? चलो जांचते हैं:

हम कमी सूत्रों के अनुसार काम करते हैं:
समीकरण में प्रतिस्थापित करें:
आइए सब कुछ कोसाइन के संदर्भ में फिर से लिखें, ताकि प्रतिस्थापन करना अधिक सुविधाजनक हो:
अब प्रतिस्थापन करना आसान है:
यह स्पष्ट है कि यह एक बाह्य मूल है, क्योंकि समीकरण का कोई हल नहीं है। फिर:
हम उन जड़ों की तलाश कर रहे हैं जिनकी हमें अंतराल में आवश्यकता है
उत्तर: ।

यहाँ प्रतिस्थापन तुरंत दिखाई देता है:

तो कोई


	- फिट बैठता है!	- फिट बैठता है!
	- फिट बैठता है!	- फिट बैठता है!
	- बहुत!	- बहुत अधिक!

उत्तर:

खैर, अब बस! लेकिन त्रिकोणमितीय समीकरणों का समाधान यहीं समाप्त नहीं होता है, हम सबसे कठिन मामलों के साथ रह जाते हैं: जब समीकरणों या विभिन्न प्रकार के "जटिल भाजक" में तर्कहीनता होती है। हम विचार करेंगे कि उन्नत स्तर के लिए लेख में ऐसे कार्यों को कैसे हल किया जाए।

उन्नत स्तर, उच्च स्तर

पिछले दो लेखों में चर्चा किए गए त्रिकोणमितीय समीकरणों के अलावा, हम समीकरणों के एक अन्य वर्ग पर भी विचार करेंगे, जिसके लिए और भी अधिक सावधानीपूर्वक विश्लेषण की आवश्यकता होती है। इन त्रिकोणमितीय उदाहरणों में या तो अतार्किकता या हर होता है, जिससे उनका विश्लेषण करना अधिक कठिन हो जाता है।... हालाँकि, आप परीक्षा के पेपर के भाग सी में इन समीकरणों को अच्छी तरह से देख सकते हैं। हालांकि, एक चांदी का अस्तर है: ऐसे समीकरणों के लिए, एक नियम के रूप में, यह सवाल नहीं उठाया जाता है कि इसकी जड़ें किस अंतराल से संबंधित हैं। आइए झाड़ी के चारों ओर न मारें, बल्कि केवल त्रिकोणमितीय उदाहरण हैं।

उदाहरण 1।

समीकरण को हल करें और उस खंड से संबंधित मूल खोजें।

समाधान:

हमारे पास एक भाजक है जो शून्य नहीं होना चाहिए! फिर इस समीकरण को हल करना सिस्टम को हल करने के समान है

आइए प्रत्येक समीकरण को हल करें:

और अब दूसरा:

अब एक नजर डालते हैं सीरीज पर:

यह स्पष्ट है कि विकल्प हमारे अनुकूल नहीं है, क्योंकि इस मामले में हर को शून्य कर दिया गया है (दूसरे समीकरण की जड़ों के लिए सूत्र देखें)

यदि, तथापि, तो सब कुछ क्रम में है, और हर शून्य नहीं है! तब समीकरण की जड़ें इस प्रकार हैं:,।

अब हम अंतराल से संबंधित जड़ों का चयन करते हैं।


	- योग्य नहीं	- फिट बैठता है
	- फिट बैठता है	- फिट बैठता है
	पाशविक बल	पाशविक बल

फिर जड़ें इस प्रकार हैं:

आप देखते हैं, यहां तक कि एक भाजक के रूप में एक छोटे से शोर की उपस्थिति ने समीकरण के समाधान को महत्वपूर्ण रूप से प्रभावित किया: हमने जड़ों की एक श्रृंखला को गिरा दिया जो कि शून्य को शून्य करता है। यदि आप तर्कहीनता वाले त्रिकोणमितीय उदाहरण देखते हैं तो स्थिति और भी कठिन हो सकती है।

उदाहरण 2।

प्रश्न हल करें:

समाधान:

खैर, कम से कम जड़ों को चुनने की कोई जरूरत नहीं है, और यह अच्छा है! आइए पहले तर्कहीनता की परवाह किए बिना समीकरण को हल करें:

यही बात है न? नहीं, अफसोस, यह बहुत आसान होगा! यह याद रखना चाहिए कि केवल गैर-ऋणात्मक संख्याएं ही जड़ के नीचे हो सकती हैं। फिर:

इस असमानता का समाधान:

अब यह पता लगाना बाकी है कि क्या पहले समीकरण की कुछ जड़ें गलती से वहां पहुंच गई हैं जहां असमानता संतुष्ट नहीं है।

ऐसा करने के लिए, आप फिर से तालिका का उपयोग कर सकते हैं:


	: , लेकिन	नहीं!
		हां!
		हां!

इस प्रकार, जड़ों में से एक मुझसे "गिर गया"! डालने से पता चलता है। तब उत्तर इस प्रकार लिखा जा सकता है:

उत्तर:

आप देखिए, जड़ को और भी अधिक ध्यान देने की आवश्यकता है! मामलों को जटिल करने के लिए: अब मुझे रूट के नीचे एक त्रिकोणमितीय कार्य करने दें।

उदाहरण 3.

पहले की तरह: पहले हम प्रत्येक को अलग-अलग हल करेंगे, और फिर हम सोचेंगे कि हमने क्या किया है।

अब दूसरा समीकरण:

अब सबसे कठिन बात यह पता लगाना है कि क्या अंकगणितीय मूल के तहत नकारात्मक मान प्राप्त होते हैं यदि हम जड़ों को पहले समीकरण से प्रतिस्थापित करते हैं:

संख्या को रेडियन के रूप में समझा जाना चाहिए। चूंकि रेडियन डिग्री के बारे में हैं, रेडियन डिग्री के बारे में हैं। यह दूसरी तिमाही का कोना है। दूसरी तिमाही की कोज्या का चिन्ह क्या है? घटा और साइन? एक से अधिक। तो अभिव्यक्ति के बारे में क्या कहा जा सकता है:

यह शून्य से कम है!

इसका मतलब है कि यह समीकरण की जड़ नहीं है।

अब बारी है।

आइए इस संख्या की तुलना शून्य से करें।

कोटैंजेंट 1 तिमाही में घटने वाला एक फ़ंक्शन है (तर्क जितना छोटा होगा, कोटेंजेंट उतना ही बड़ा होगा)। रेडियन मोटे तौर पर डिग्री हैं। एक ही समय में

तब से, तब से, और इसलिए
,

उत्तर: ।

क्या यह और भी कठिन हो सकता है? आपका स्वागत है! यह अधिक कठिन होगा यदि त्रिकोणमितीय फलन अभी भी मूल के नीचे है, और समीकरण का दूसरा भाग फिर से त्रिकोणमितीय फलन है।

अधिक त्रिकोणमितीय उदाहरण बेहतर, आगे देखें:

उदाहरण 4.

सीमित कोसाइन के कारण जड़ उपयुक्त नहीं है

अब दूसरा:

उसी समय, जड़ की परिभाषा के अनुसार:

हमें यूनिट सर्कल को याद रखना चाहिए: अर्थात्, वे क्वार्टर जहां ज्या शून्य से कम है। वे कौन से क्वार्टर हैं? तीसरा और चौथा। तब हम पहले समीकरण के उन हलों में रुचि लेंगे जो तीसरी या चौथी तिमाही में स्थित हैं।

पहली श्रृंखला तीसरी और चौथी तिमाही के चौराहे पर जड़ें पैदा करती है। दूसरी श्रृंखला, जो इसके बिल्कुल विपरीत है, पहली और दूसरी तिमाही की सीमा पर पड़ी जड़ों को जन्म देती है। इसलिए यह सीरीज हमें शोभा नहीं देती।

उत्तर: ,

और फिर "कठिन तर्कहीनता" के साथ त्रिकोणमितीय उदाहरण... न केवल हमारे पास फिर से रूट के नीचे त्रिकोणमितीय फ़ंक्शन है, बल्कि अब यह हर में भी है!

उदाहरण 5.

खैर, कुछ नहीं किया जा सकता - हम पहले की तरह काम करते हैं।

अब हम हर के साथ काम करते हैं:

मैं त्रिकोणमितीय असमानता को हल नहीं करना चाहता, और इसलिए मैं चालाकी से कार्य करूंगा: मैं अपनी जड़ों की श्रृंखला को असमानता में ले जाऊंगा और प्रतिस्थापित करूंगा:

अगर - सम, तो हमारे पास है:

तब से, देखने के सभी कोण चौथी तिमाही में हैं। और फिर से पवित्र प्रश्न: चौथी तिमाही में साइनस का चिन्ह क्या है? नकारात्मक। फिर असमानता

यदि यह विषम है, तो:

कोना किस क्वार्टर में है? यह दूसरी तिमाही का कोना है। फिर सभी कोने फिर से दूसरी तिमाही के कोने हैं। वहां साइनस पॉजिटिव है। बस आपको क्या चाहिए! इसलिए, श्रृंखला:

फिट बैठता है!

जड़ों की दूसरी श्रृंखला के साथ इसी तरह व्यवहार करें:

हम अपनी असमानता में स्थानापन्न करते हैं:

अगर - सम, तो

पहली तिमाही के कोने। वहाँ साइनस सकारात्मक है, इसलिए श्रृंखला उपयुक्त है। अब अगर - विषम, तब:

भी फिट बैठता है!

खैर, अब हम उत्तर लिखते हैं!

उत्तर:

खैर, यह शायद सबसे अधिक समय लेने वाला मामला था। अब मैं आपको आपके समाधान के लिए समस्याएं पेश करता हूं।

व्यायाम

खंड से संबंधित समीकरण के सभी मूलों को हल करें और खोजें।

समाधान:

पहला समीकरण:
या
ओडीजेड रूट:
दूसरा समीकरण:
अंतराल से संबंधित जड़ों का चयन
उत्तर:

या
या
लेकिन

विचार करना:। अगर - सम, तो
- योग्य नहीं!
अगर - अजीब,: - फिट बैठता है!
इसका मतलब है कि हमारे समीकरण में जड़ों की निम्नलिखित श्रृंखला है:
या
अंतराल में जड़ों का चयन:


	- योग्य नहीं	- फिट बैठता है
	- फिट बैठता है	- बहुत
	- फिट बैठता है	बहुत

उत्तर: , ।

या
चूंकि, स्पर्शरेखा परिभाषित नहीं है। हम जड़ों की इस श्रृंखला को तुरंत त्याग देते हैं!

दूसरे भाग:

वहीं, ODZ के अनुसार यह आवश्यक है कि

हम पहले समीकरण में पाए गए जड़ों की जांच करते हैं:

यदि संकेत है:

पहली तिमाही के कोने जहां स्पर्शरेखा सकारात्मक है। फिट नहीं है!
यदि संकेत है:

चौथा चौथाई कोण। वहां स्पर्शरेखा ऋणात्मक है। फिट बैठता है। हम उत्तर लिखते हैं:

उत्तर: , ।

हमने इस लेख में जटिल त्रिकोणमितीय उदाहरणों को एक साथ शामिल किया है, लेकिन आपको समीकरणों को स्वयं हल करना चाहिए।

सारांश और बुनियादी सूत्र

एक त्रिकोणमितीय समीकरण एक समीकरण है जिसमें अज्ञात त्रिकोणमितीय फ़ंक्शन के संकेत के तहत सख्ती से होता है।

त्रिकोणमितीय समीकरणों को हल करने के दो तरीके हैं:

पहला तरीका सूत्रों का उपयोग कर रहा है।

दूसरा तरीका त्रिकोणमितीय सर्कल के माध्यम से है।

आपको कोणों को मापने, उनकी साइन, कोसाइन और बहुत कुछ खोजने की अनुमति देता है।

गणित में एकीकृत राज्य परीक्षा के प्रोफाइल स्तर की तैयारी। त्रिकोणमिति पर उपयोगी सामग्री, बड़े सैद्धांतिक वीडियो व्याख्यान, समस्याओं का वीडियो विश्लेषण और पिछले वर्षों से असाइनमेंट का चयन।

उपयोगी सामग्री

वीडियो चयन और ऑनलाइन पाठ्यक्रम

त्रिकोणमितीय सूत्र

त्रिकोणमितीय सूत्रों का ज्यामितीय चित्रण

आर्क कार्य करता है। सरलतम त्रिकोणमितीय समीकरण

त्रिकोणमितीय समीकरण

समस्याओं को हल करने के लिए आवश्यक सिद्धांत।
a) समीकरण $ 7 \ cos ^ 2 x - \ cos x - 8 = 0 $ को हल करें।
बी) इस समीकरण की सभी जड़ों को खोजें जो अंतराल $ \ बाएँ [- \ dfrac (7 \ pi) (2); - \ dfrac (3 \ pi) (2) \ right] $।
a) समीकरण $ \ dfrac (6) (\ cos ^ 2 x) - \ dfrac (7) (\ cos x) + 1 = 0 $ को हल करें।
बी) इस समीकरण की सभी जड़ों को खोजें जो अंतराल $ \ बाएँ [-3 \ pi; - \ पीआई \ दाएं] $।
समीकरण $ \ sin \ sqrt (16 - x ^ 2) = \ dfrac12 $ को हल करें।
a) समीकरण $ 2 \ cos 2x - 12 \ cos x + 7 = 0 $ को हल करें।
बी) इस समीकरण की सभी जड़ों को खोजें जो अंतराल $ \ बाएँ [- \ pi; \ dfrac (5 \ pi) (2) \ right] $.
a) समीकरण $ \ dfrac (5) (\ mathrm (tg) ^ 2 x) - \ dfrac (19) (\ sin x) + 17 = 0 $ को हल करें।
समीकरण को हल करें $ \ dfrac (2 \ cos ^ 3 x + 3 \ cos ^ 2 x + \ cos x) (\ sqrt (\ mathrm (ctg) x)) = 0 $।
समीकरण को हल करें $ \ dfrac (\ mathrm (tg) ^ 3x - \ mathrm (tg) x) (\ sqrt (- \ sin x)) = 0 $।
बी) इस समीकरण की सभी जड़ों को खोजें जो अंतराल $ \ बाएँ [- \ dfrac (5 \ pi) (2); - \ पीआई \ दाएं) $।
a) समीकरण $ \ cos 2x = \ sin \ left (\ dfrac (3 \ pi) (2) - x \ right) $ को हल करें।
बी) इस समीकरण की सभी जड़ों को खोजें जो अंतराल से संबंधित हैं $ \ बाएँ [\ dfrac (3 \ pi) (2); \ dfrac (5 \ pi) (2) \ right] $.
a) समीकरण $ 2 \ sin ^ 2 \ बाएँ (\ dfrac (3 \ pi) (2) + x \ दाएँ) = \ sqrt3 \ cos x $ को हल करें।
बी) इस समीकरण की सभी जड़ों को खोजें जो अंतराल $ \ बाएँ [- \ dfrac (7 \ pi) (2); -2 \ पीआई \ दाएं] $।

कार्यों का वीडियो विश्लेषण

बी) इस समीकरण की सभी जड़ों को खोजें जो खंड $ \ बाएँ [\ sqrt (3); \ sqrt (20) \ दाएँ] $।

बी) इस समीकरण के सभी मूल खोजें जो खंड $ \ बाएँ [- \ dfrac (9 \ pi) (2) से संबंधित हैं; -3 \ पीआई \ दाएं] $।

बी) इस समीकरण की सभी जड़ों को खोजें जो खंड $ \ बाएँ [- \ sqrt (3); \ sqrt (30) \ दाएँ] $।

a) समीकरण $ \ cos 2x = 1 - \ cos \ left (\ dfrac (\ pi) (2) - x \ right) $ को हल करें।
बी) इस समीकरण की सभी जड़ों को खोजें जो अंतराल $ \ बाएँ [- \ dfrac (5 \ pi) (2); - \ पीआई \ दाएं) $।

a) समीकरण $ \ cos ^ 2 (\ pi - x) - \ sin \ बाएँ (x + \ dfrac (3 \ pi) (2) \ right) = 0 $ को हल करें।
बी) इस समीकरण की सभी जड़ों को खोजें जो अंतराल $ \ बाएँ [\ dfrac (5 \ pi) (2); 4 \ पीआई \ दाएं] $।

बी) इस समीकरण की सभी जड़ों को खोजें जो अंतराल $ \ बाएँ [\ log_5 2; \ log_5 20 \ सही] $.

a) समीकरण $8 \ sin ^ 2 x + 2 \ sqrt (3) \ cos \ left (\ dfrac (3 \ pi) (2) - x \ right) = 9 $ को हल करें।
बी) इस समीकरण की सभी जड़ों को खोजें जो अंतराल $ \ बाएँ [- \ dfrac (5 \ pi) (2); - \ पीआई \ दाएं] $।

a) समीकरण $ 2 \ log_3 ^ 2 (2 \ cos x) - 5 \ log_3 (2 \ cos x) + 2 = 0 $ को हल करें।
बी) इस समीकरण की सभी जड़ों को खोजें जो अंतराल $ \ बाएँ [\ pi; \ dfrac (5 \ pi) (2) \ right] $.

a) समीकरण को हल करें $ \ बाएँ (\ dfrac (1) (49) \ दाएँ) ^ (\ sin x) = 7 ^ (2 \ sin 2x) $।
बी) इस समीकरण की सभी जड़ों को खोजें जो अंतराल से संबंधित हैं $ \ बाएँ [\ dfrac (3 \ pi) (2); 3 \ पीआई \ दाएं] $।

a) समीकरण को हल करें $ \ sin x + \ बाएँ (\ cos \ dfrac (x) (2) - \ sin \ dfrac (x) (2) \ दाएँ) \ बाएँ (\ cos \ dfrac (x) (2) + \ sin \ dfrac (x) (2) \ right) = 0 $।
बी) इस समीकरण की सभी जड़ों को खोजें जो अंतराल $ \ बाएँ [\ pi; \ dfrac (5 \ pi) (2) \ right] $.

ए) समीकरण $ \ log_4 (\ sin x + \ sin 2x + 16) = 2 $ को हल करें।
बी) इस समीकरण की सभी जड़ों को खोजें जो अंतराल $ \ बाएँ [-4 \ pi; - \ dfrac (5 \ pi) (2) \ right] $।

पिछले वर्षों से असाइनमेंट का चयन

ए) समीकरण $ \ dfrac (\ sin x) (\ sin ^ 2 \ dfrac (x) (2)) = 4 \ cos ^ 2 \ dfrac (x) (2) $ हल करें।
बी) इस समीकरण के सभी मूल खोजें जो खंड $ \ बाएँ [- \ dfrac (9 \ pi) (2) से संबंधित हैं; -3 \ पीआई \ दाएं] $। (USE-2018। प्रारंभिक लहर)
a) समीकरण $ \ sqrt (x ^ 3 - 4x ^ 2 - 10x + 29) = 3 - x $ को हल करें।
बी) इस समीकरण की सभी जड़ों को खोजें जो खंड $ \ बाएँ [- \ sqrt (3); \ sqrt (30) \ दाएँ] $। (USE-2018. अर्ली वेव, रिजर्व डे)
a) समीकरण $ 2 \ sin ^ 2 x + \ sqrt2 \ sin \ बाएँ (x + \ dfrac (\ pi) (4) \ दाएँ) = \ cos x $ को हल करें।
बी) इस समीकरण की सभी जड़ों को खोजें जो खंड $ \ बाएँ [-2 \ pi; - \ dfrac (\ pi) (2) \ right] $. (USE-2018। मुख्य लहर)
a) समीकरण $ \ sqrt6 \ sin ^ 2 x + \ cos x = 2 \ sin \ बाएँ (x + \ dfrac (\ pi) (6) \ दाएँ) $ को हल करें।
बी) इस समीकरण की सभी जड़ों को खोजें जो खंड $ \ बाएँ [3 \ pi; \ dfrac (9 \ pi) (2) \ right] $. (USE-2018। मुख्य लहर)
a) समीकरण $ \ sin x + 2 \ sin \ बाएँ (2x + \ dfrac (\ pi) (6) \ दाएँ) = \ sqrt3 \ sin 2x + 1 $ को हल करें।
बी) इस समीकरण की सभी जड़ों को खोजें जो खंड $ \ बाएँ [- \ dfrac (7 \ pi) (2); -2 \ पीआई \ दाएं] $। (USE-2018। मुख्य लहर)
a) समीकरण $ \ cos ^ 2 x + \ sin x = \ sqrt2 \ sin \ बाएँ (x + \ dfrac (\ pi) (4) \ right) $ हल करें।
बी) इस समीकरण की सभी जड़ों को खोजें जो खंड $ \ बाएँ [-4 \ pi; - \ dfrac (5 \ pi) (2) \ right] $। (USE-2018। मुख्य लहर)
a) समीकरण $ 2 \ sin \ बाएँ (2x + \ dfrac (\ pi) (3) \ दाएँ) - \ sqrt (3) \ sin x = \ sin 2x + \ sqrt3 $ को हल करें।
ए) समीकरण $ 2 \ sqrt3 \ sin \ बाएँ (x + \ dfrac (\ pi) (3) \ दाएँ) - \ cos 2x = 3 \ cos x - 1 $ हल करें।
बी) इस समीकरण की सभी जड़ों को खोजें जो खंड $ \ बाएँ [2 \ pi; \ dfrac (7 \ pi) (2) \ right] $. (USE-2018। मुख्य लहर)
a) समीकरण $ 2 \ sin \ बाएँ (2x + \ dfrac (\ pi) (6) \ दाएँ) - \ cos x = \ sqrt3 \ sin 2x - 1 $ को हल करें।
बी) इस समीकरण के सभी मूल खोजें जो खंड $ \ बाएँ [\ dfrac (5 \ pi) (2); 4 \ पीआई \ दाएं] $। (USE-2018। मुख्य लहर)
a) समीकरण $ \ sqrt2 \ sin \ बाएँ (\ dfrac (\ pi) (4) + x \ दाएँ) + \ cos 2x = \ sin x - 1 $ को हल करें।
बी) इस समीकरण की सभी जड़ों को खोजें जो खंड $ \ बाएँ [\ dfrac (7 \ pi) (2); 5 \ पीआई \ दाएं] $। (USE-2018। मुख्य लहर)
a) समीकरण को हल करें $ \ sqrt2 \ sin \ बाएँ (2x + \ dfrac (\ pi) (4) \ दाएँ) + \ sqrt2 \ cos x = \ sin 2x - 1 $।
बी) इस समीकरण की सभी जड़ों को खोजें जो खंड $ \ बाएँ [- \ dfrac (5 \ pi) (2); - \ पीआई \ दाएं] $। (USE-2018। मुख्य लहर)
a) समीकरण $ 2 \ sin \ बाएँ (x + \ dfrac (\ pi) (3) \ दाएँ) + \ cos 2x = \ sqrt3 \ cos x + 1 $ को हल करें।
बी) इस समीकरण की सभी जड़ों को खोजें जो खंड $ \ बाएँ [-3 \ pi; - \ dfrac (3 \ pi) (2) \ right] $। (USE-2018। मुख्य लहर)
बी) इस समीकरण की सभी जड़ों को खोजें जो खंड $ \ बाएँ [\ pi; \ dfrac (5 \ pi) (2) \ right] $. (USE-2018। मुख्य लहर)
a) समीकरण $ 2 \ sin \ बाएँ (x + \ dfrac (\ pi) (4) \ दाएँ) + \ cos 2x = \ sqrt2 \ cos x + 1 $ को हल करें।
बी) इस समीकरण की सभी जड़ों को खोजें जो खंड $ \ बाएँ [\ pi; \ dfrac (5 \ pi) (2) \ right] $. (USE-2018। मुख्य लहर, आरक्षित दिवस)
ए) समीकरण $ 2 \ cos x - \ sqrt3 \ sin ^ 2 x = 2 \ cos ^ 3 x $ को हल करें।
बी) इस समीकरण की सभी जड़ों को खोजें जो खंड $ \ बाएँ [- \ dfrac (7 \ pi) (2); -2 \ पीआई \ दाएं] $। (USE-2018। मुख्य लहर, आरक्षित दिवस)
ए) समीकरण $ 2 \ cos x + \ sin ^ 2 x = 2 \ cos ^ 3 x $ हल करें।
बी) इस समीकरण के सभी मूल खोजें जो खंड $ \ बाएँ [- \ dfrac (9 \ pi) (2) से संबंधित हैं; -3 \ पीआई \ दाएं] $। (USE-2018। मुख्य लहर, आरक्षित दिवस)
a) समीकरण $ 2 \ sqrt2 \ sin \ बाएँ (x + \ dfrac (\ pi) (3) \ दाएँ) + 2 \ cos ^ 2 x = 2 + \ sqrt6 \ cos x $ को हल करें।
बी) इस समीकरण की सभी जड़ों को खोजें जो खंड $ \ बाएँ [-3 \ pi; - \ dfrac (3 \ pi) (2) \ right] $। (USE-2018। मुख्य लहर, आरक्षित दिवस)
a) समीकरण $ x - 3 \ sqrt (x - 1) + 1 = 0 $ को हल करें।
बी) इस समीकरण की सभी जड़ों को खोजें जो खंड $ \ बाएँ [\ sqrt (3); \ sqrt (20) \ दाएँ] $। (USE-2018। मुख्य लहर, आरक्षित दिवस)
a) समीकरण $ 2x \ cos x - 8 \ cos x + x - 4 = 0 $ को हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [- \ dfrac (\ pi) (2); \ \ pi \ right] $ से संबंधित हैं। (USE-2017, मेन वेव, रिजर्व डे)
a) समीकरण $ \ log_3 (x ^ 2 - 2x) = 1 $ को हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [\ log_2 0 (,) 2; \ \ log_2 5 \ right] $ से संबंधित हैं। (USE-2017, मेन वेव, रिजर्व डे)
a) समीकरण $ \ log_3 (x ^ 2 - 24x) = 4 $ को हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [\ log_2 0 (,) 1; \ 12 \ sqrt (5) \ right] $ से संबंधित हैं। (USE-2017, मेन वेव, रिजर्व डे)
a) समीकरण $ 0 (,) 4 ^ (\ sin x) + 2 (,) 5 ^ (\ sin x) = 2 $ को हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [2 \ pi; \ \ dfrac (7 \ pi) (2) \ right] $ से संबंधित हैं। (USE-2017, मुख्य लहर)
a) समीकरण $ \ log_8 \ बाएँ (7 \ sqrt (3) \ sin x - \ cos 2x - 10 \ right) = 0 $ को हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [\ dfrac (3 \ pi) (2); \ 3 \ pi \ right] $ से संबंधित हैं। (USE-2017, मुख्य लहर)
a) समीकरण $ \ log_4 \ बाएँ (2 ^ (2x) - \ sqrt (3) \ cos x - 6 \ sin ^ 2 x \ दाएँ) = x $ को हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [\ dfrac (5 \ pi) (2); \ 4 \ pi \ right] $ से संबंधित हैं। (USE-2017, मुख्य लहर)
ए) समीकरण को हल करें $ 2 \ log_2 ^ 2 \ बाएँ (\ sin x \ दाएँ) - 5 \ log_2 \ बाएँ (\ sin x \ दाएँ) - 3 = 0 $।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [- 3 \ pi; \ - \ dfrac (3 \ pi) (2) \ right] $ से संबंधित हैं। (USE-2017, मुख्य लहर)
a) समीकरण $81 ^ (\ cos x) - 12 \ cdot 9 ^ (\ cos x) + 27 = 0 $ को हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [- 4 \ pi; \ - \ dfrac (5 \ pi) (2) \ right] $ से संबंधित हैं। (USE-2017, मुख्य लहर)
ए) समीकरण $ 8 ^ x - 9 \ cdot 2 ^ (x + 1) + 2 ^ (5 - x) = 0 $ हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [\ log_5 2; \ \ log_5 20 \ right] $ से संबंधित हैं। (USE-2017, अर्ली वेव)
ए) समीकरण $ 2 \ लॉग ^ 2_9 x - 3 \ log_9 x + 1 = 0 $ हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [\ sqrt (10); \ \ sqrt (99) \ दाएँ] $ से संबंधित हैं। (USE-2016, मुख्य लहर, आरक्षित दिवस)
ए) समीकरण $ 6 \ लॉग ^ 2_8 x - 5 \ log_8 x + 1 = 0 $ को हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [2; \ 2 (,) 5 \ दाएँ] $ से संबंधित हैं। (USE-2016, मुख्य लहर, आरक्षित दिवस)
a) समीकरण $ \ sin 2x = 2 \ sin x + \ sin \ बाएँ (x + \ dfrac (3 \ pi) (2) \ दाएँ) + 1 $ को हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो सेगमेंट $ \ लेफ्ट [-4 \ pi; \ - \ dfrac (5 \ pi) (2) \ right] $ से संबंधित हैं। (USE-2016, मुख्य लहर, आरक्षित दिवस)
a) समीकरण $ 2 \ cos ^ 2 x + 1 = 2 \ sqrt (2) \ cos \ बाएँ (\ dfrac (3 \ pi) (2) - x \ दाएँ) $ को हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [\ dfrac (3 \ pi) (2); \ 3 \ pi \ right] $ से संबंधित हैं। (USE-2016, मुख्य लहर)
a) समीकरण $ 2 \ log ^ 2_2 (2 \ cos x) - 9 \ log_2 (2 \ cos x) + 4 = 0 $ को हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [-2 \ pi; \ - \ dfrac (\ pi) (2) \ right] $ से संबंधित हैं। (USE-2016, मुख्य लहर)
ए) समीकरण $ 8 ^ x - 7 \ cdot 4 ^ x - 2 ^ (x + 4) + 112 = 0 $ हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [\ log_2 5; \ \ log_2 11 \ right] $ से संबंधित हैं। (USE-2016, अर्ली वेव)
a) समीकरण $ \ cos 2x + \ cos ^ 2 \ बाएँ (\ dfrac (3 \ pi) (2) - x \ दाएँ) = 0.25 $ को हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो सेगमेंट $ \ लेफ्ट [-4 \ pi; \ - \ dfrac (5 \ pi) (2) \ right] $ से संबंधित हैं। (USE-2016, अर्ली वेव)
ए) समीकरण $ \ dfrac (13 \ sin ^ 2 x - 5 \ sin x) (13 \ cos x + 12) = 0 $ हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ right] $ से संबंधित हैं। (USE-2016, अर्ली वेव)
a) समीकरण $ \ dfrac (\ sin2x) (\ sin \ left (\ dfrac (7 \ pi) (2) - x \ right)) = \ sqrt (2) $ को हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ $ से संबंधित हैं। (USE-2015, मुख्य लहर)
a) समीकरण $4 \ sin ^ 2 x = \ mathrm (tg) x $ को हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [- \ pi; \ 0 \ दाएँ] $ से संबंधित हैं। (USE-2015, मुख्य लहर)
ए) समीकरण $ 3 \ cos 2x - 5 \ sin x + 1 = 0 $ को हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [\ pi; \ \ dfrac (5 \ pi) (2) \ right] $ से संबंधित हैं। (USE-2015, मुख्य लहर)
a) समीकरण $ \ cos 2x - 5 \ sqrt (2) \ cos x - 5 = 0 $ को हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ right] $ से संबंधित हैं। (USE-2015, मुख्य लहर)
a) समीकरण $ \ sin 2x + \ sqrt (2) \ sin x = 2 \ cos x + \ sqrt (2) $ को हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [\ pi; \ \ dfrac (5 \ pi) (2) \ right] $ से संबंधित हैं। (USE-2015, अर्ली वेव)
ए) समीकरण $ 2 \ cos ^ 3 x - \ cos ^ 2 x + 2 \ cos x - 1 = 0 $ को हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [2 \ pi; \ \ dfrac (7 \ pi) (2) \ right] $ से संबंधित हैं। (USE-2015, अर्ली वेव)
a) समीकरण $ \ mathrm (tg) ^ 2 x + (1 + \ sqrt (3)) \ mathrm (tg) x + \ sqrt (3) = 0 $ को हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [\ dfrac (5 \ pi) (2); \ 4 \ पीआई \ दाएं] $। (USE-2014, मुख्य लहर)
a) समीकरण $ 2 \ sqrt (3) \ cos ^ 2 \ बाएँ (\ dfrac (3 \ pi) (2) + x \ दाएँ) - \ sin 2x = 0 $ को हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [\ dfrac (3 \ pi) (2); \ 3 \ पीआई \ दाएं] $। (USE-2014, मुख्य लहर)
a) समीकरण $ \ cos 2x + \ sqrt (2) \ sin \ left (\ dfrac (\ pi) (2) + x \ right) + 1 = 0 $ को हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ right] $। (USE-2014, मुख्य लहर)
a) समीकरण $ - \ sqrt (2) \ sin \ बाएँ (- \ dfrac (5 \ pi) (2) + x \ दाएँ) \ cdot \ sin x = \ cos x $ को हल करें।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [\ dfrac (9 \ pi) (2) से संबंधित हैं; \ 6 \ पीआई \ दाएं] $। (USE-2014, अर्ली वेव)
a) समीकरण को हल करें $ \ sin 2x = \ sin \ left (\ dfrac (\ pi) (2) + x \ right) $।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [- \ dfrac (7 \ pi) (2) से संबंधित हैं; \ - \ dfrac (5 \ pi) (2) \ right] $। (USE-2013, मुख्य लहर)
a) समीकरण को हल करें $6 \ sin ^ 2 x + 5 \ sin \ left (\ dfrac (\ pi) (2) - x \ right) - 2 = 0 $।
बी) इस समीकरण की जड़ों को इंगित करें जो खंड $ \ बाएँ [-5 \ pi; \ - \ dfrac (7 \ pi) (2) \ right] $। (USE-2012, दूसरी लहर)

पाठ का उद्देश्य:

ए) सरलतम त्रिकोणमितीय समीकरणों को हल करने की क्षमता को समेकित करने के लिए;

बी) दिए गए अंतराल से त्रिकोणमितीय समीकरणों के मूल चुनना सिखाएं

कक्षाओं के दौरान।

1. ज्ञान की प्राप्ति।

a) गृहकार्य की जाँच करना: कक्षा को एक अनुमानित गृहकार्य दिया गया था - समीकरण को हल करने और दिए गए अंतराल से जड़ों का चयन करने का एक तरीका खोजने के लिए।

1)कोस एक्स= -0.5, जहां xI [-]। उत्तर:.

2) पाप एक्स=, जहां xI. उत्तर: ; ...

3) कॉस 2 एक्स= -, जहां I. उत्तर:

छात्र बोर्ड पर समाधान लिखते हैं, कोई ग्राफ का उपयोग करता है, कोई चयन विधि का उपयोग करता है।

इस समय कक्षा मौखिक रूप से काम करता है।

अभिव्यक्ति का अर्थ खोजें:

ए) टीजी - पाप + कॉस + पाप। उत्तर 1।

b) 2arccos 0 + 3 arccos 1. उत्तर: ?

ग) आर्क्सिन + आर्क्सिन। उत्तर:.

d) 5 आर्कटान (-) - आर्ककोस (-)। उत्तर:-.

- आइए अपना होमवर्क जांचें, अपना होमवर्क नोटबुक खोलें।

आप में से कुछ लोगों ने एक उपयुक्त विधि द्वारा समाधान खोजा है, और कुछ ने एक ग्राफ द्वारा।

2. इन कार्यों को कैसे हल करें और समस्या कथन, यानी विषय का संदेश और पाठ का उद्देश्य पर निष्कर्ष।

- क) यदि बड़ा अंतराल दिया जाए तो चयन की सहायता से हल करना कठिन होता है।

- बी) ग्राफिकल विधि सटीक परिणाम नहीं देती है, सत्यापन की आवश्यकता होती है, और इसमें बहुत समय लगता है।

- इसलिए, कम से कम एक और तरीका होना चाहिए, सबसे सार्वभौमिक - आइए इसे खोजने का प्रयास करें। तो आज हम कक्षा में क्या करने जा रहे हैं? (किसी दिए गए अंतराल पर त्रिकोणमितीय समीकरण के मूल चुनना सीखें।)

- उदाहरण 1 (छात्र ब्लैकबोर्ड पर जाता है)

क्योंकि एक्स= -0.5, जहां xI [-]।

प्रश्न: इस कार्य का उत्तर किस पर निर्भर करता है? (समीकरण के व्यापक हल से। आइए हम हल को सामान्य रूप में लिखें)। निर्णय बोर्ड पर लिखा है

= + 2? k, जहाँ k R.

- आइए इस समाधान को एक सेट के रूप में लिखें:

- आप क्या सोचते हैं, समाधान के किस रिकॉर्ड के लिए अंतराल में जड़ों को चुनना सुविधाजनक है? (दूसरी प्रविष्टि से)। लेकिन यह फिर से एक चयन विधि है। सही उत्तर पाने के लिए हमें क्या जानने की आवश्यकता है? (आपको k के मान जानने की आवश्यकता है)।

(आइए k को खोजने के लिए एक गणितीय मॉडल बनाते हैं)।



चूँकि kI Z, तो k = 0, इसलिए एक्स= =	यह असमानता दर्शाती है कि k का कोई पूर्णांक मान नहीं है।

निष्कर्ष:किसी त्रिकोणमितीय समीकरण को हल करते समय दिए गए अंतराल से मूलों का चयन करने के लिए, आपको यह करना होगा:

फॉर्म के समीकरण को हल करने के लिए पाप एक्स = ए, कॉस एक्स = एसमीकरण के मूलों को जड़ों की दो श्रृंखलाओं के रूप में लिखना अधिक सुविधाजनक होता है।
फॉर्म के समीकरणों को हल करने के लिए टीजी एक्स = ए, सीटीजी एक्स = एजड़ों के लिए सामान्य सूत्र लिखिए।
दोहरी असमानता के रूप में प्रत्येक समाधान के लिए एक गणितीय मॉडल तैयार करें और पैरामीटर k या n का पूर्णांक मान ज्ञात करें।
इन मानों को मूल सूत्र में प्रतिस्थापित करें और उनकी गणना करें।

3. एंकरिंग।

प्राप्त एल्गोरिथम का उपयोग करके गृहकार्य से उदाहरण 2 और 3 को हल करें। उसी समय, दो छात्र ब्लैकबोर्ड पर काम करते हैं, उसके बाद काम की जाँच करते हैं।

इस लेख में मैं 2 तरीके समझाने की कोशिश करूंगा त्रिकोणमितीय समीकरण में जड़ों का चयन: असमानताओं का उपयोग करना और त्रिकोणमितीय वृत्त का उपयोग करना। आइए सीधे एक उदाहरण के उदाहरण पर चलते हैं और मामले से निपटते हैं।

ए) समीकरण हल करें sqrt (2) cos ^ 2x = sin (Pi / 2 + x)
बी) अंतराल से संबंधित इस समीकरण की सभी जड़ें खोजें [-7Pi / 2; -2 पीआई]

आइए बिंदु ए को हल करें।

हम ज्या पाप (Pi / 2 + x) = cos (x) के लिए न्यूनीकरण सूत्र का उपयोग करते हैं

वर्ग (2) cos ^ 2x = cosx

वर्ग (2) cos ^ 2x - cosx = 0

Cosx (वर्ग (2) cosx - 1) = 0

X1 = पाई / 2 + पिन, n Z

वर्ग (2) cosx - 1 = 0

Cosx = 1 / sqrt (2)

Cosx = sqrt (2) / 2

X2 = आर्ककोस (वर्ग (2) / 2) + 2 पिन, n Z
x3 = -arccos (वर्ग (2) / 2) + 2 पिन, n Z

X2 = पाई / 4 + 2पिन, n Z
x3 = -Pi / 4 + 2पिन, n Z

आइए बिंदु बी को हल करें।

1) असमानताओं का उपयोग करके जड़ों का चयन

यहां सब कुछ सरलता से किया जाता है, हम प्राप्त जड़ों को दिए गए अंतराल में प्रतिस्थापित करते हैं [-7Pi / 2; -2Pi], n के लिए पूर्णांक मान ज्ञात करें।

7Pi / 2 Pi से कम या बराबर / 2 + पिन -2Pi . से कम या बराबर

सब कुछ एक बार में पाई में विभाजित करें

7/2 1/2 से कम या बराबर है + n -2 . से कम या बराबर है

7/2 - 1/2 n से कम या बराबर -2 - 1/2 . से कम या बराबर

4 से कम या n के बराबर -5/2 . से कम या बराबर

इस श्रेणी में पूर्णांक n -4 और -3 है। तो इस अंतराल से संबंधित मूल होंगे पाई/2 + पाई (-4) = -7Pi/2, Pi/2 + Pi (-3) = -5Pi/2

इसी तरह, हम दो और असमानताएँ बनाते हैं

7Pi / 2 Pi से कम या बराबर / 4 + 2Pin -2Pi . से कम या उसके बराबर
-15/8 n से कम या बराबर -9/8 . से कम या बराबर

इस अंतराल में कोई पूर्णांक n नहीं है

7Pi / 2 कम या बराबर -Pi / 4 + 2Pin -2Pi से कम या उसके बराबर
-13/8 n से कम या बराबर -7/8 . से कम या बराबर

इस अवधि में एक पूर्णांक n -1 है। तो इस अंतराल पर चयनित रूट है -Pi / 4 + 2Pi * (- 1) = -9Pi / 4।

तो उत्तर बिंदु b में: -7Pi / 2, -5Pi / 2, -9Pi / 4

2) त्रिकोणमितीय वृत्त का उपयोग करके जड़ों का चयन करना

इस पद्धति का उपयोग करने के लिए, आपको यह समझने की आवश्यकता है कि यह चक्र कैसे काम करता है। मैं इसे सरल भाषा में समझाने की कोशिश करूंगा कि मैं इसे कैसे समझता हूं। मुझे लगता है कि स्कूलों में बीजगणित के पाठों में इस विषय को शिक्षक के चतुर शब्दों, पाठ्यपुस्तकों में जटिल योगों द्वारा कई बार समझाया गया था। व्यक्तिगत रूप से, मैं इसे एक सर्कल के रूप में समझता हूं जिसे अनंत बार पार किया जा सकता है, इस तथ्य के कारण कि साइन और कोसाइन फ़ंक्शन आवधिक हैं।

चलो एक बार वामावर्त चलते हैं

चलो लगभग 2 बार वामावर्त चलते हैं

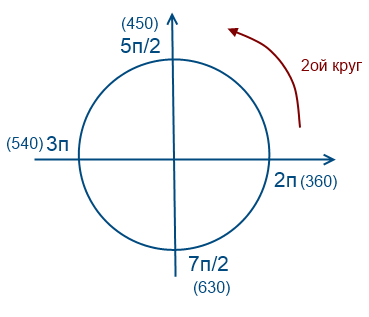
चलो लगभग 1 बार दक्षिणावर्त चलते हैं (मान नकारात्मक होंगे)

आइए अपने प्रश्न पर वापस आते हैं, हमें अंतराल में जड़ों का चयन करने की आवश्यकता है [-7Pi / 2; -2 पीआई]

नंबर -7Pi / 2 और -2Pi तक पहुंचने के लिए, आपको दो बार वामावर्त सर्कल के चारों ओर जाने की जरूरत है। इस अंतराल पर समीकरण के मूल ज्ञात करने के लिए अनुमान लगाना और स्थानापन्न करना आवश्यक है।

एक्स = पीआई / 2 + पिन पर विचार करें। इस अंतराल में x के मान के कहीं होने के लिए n का अनुमानित मान क्या है? प्रतिस्थापित करने पर, मान लीजिए -2, हमें Pi/2 - 2Pi = -3Pi / 2 मिलता है, जाहिर है यह हमारे अंतराल में शामिल नहीं है, इसलिए हम -3 से कम लेते हैं, Pi / 2 - 3Pi = -5Pi / 2, यह फिट बैठता है, आइए -4 फिर से प्रयास करें, पाई / 2 - 4Pi = -7Pi / 2 भी उपयुक्त है।

इसी तरह Pi / 4 + 2Pin और -Pi / 4 + 2Pin के लिए तर्क करने पर, हम एक और रूट -9Pi / 4 पाते हैं।

दो विधियों की तुलना।

पहली विधि (असमानताओं का उपयोग करके) अधिक विश्वसनीय और समझने में बहुत आसान है, लेकिन यदि आप वास्तव में त्रिकोणमितीय सर्कल और दूसरी चयन विधि से गंभीरता से निपटते हैं, तो जड़ों का चयन बहुत तेज़ होगा, आप लगभग 15 मिनट बचा सकते हैं परीक्षा।

ए) समीकरण हल करें:।

बी) इस समीकरण की सभी जड़ों को खोजें जो खंड से संबंधित हैं।

समस्या का समाधान

यह पाठ त्रिकोणमितीय समीकरण को हल करने के एक उदाहरण पर विचार करता है, जिसका उपयोग गणित में परीक्षा की तैयारी में टाइप C1 की समस्याओं को हल करने के लिए एक उदाहरण के रूप में किया जा सकता है।

सबसे पहले, फ़ंक्शन का दायरा निर्धारित किया जाता है - तर्क के सभी अनुमत मान। फिर, समाधान के दौरान, त्रिकोणमितीय साइन फ़ंक्शन को कमी सूत्र का उपयोग करके कोसाइन में परिवर्तित किया जाता है। इसके अलावा, समीकरण के सभी पदों को इसके बाईं ओर स्थानांतरित कर दिया जाता है, जहां सामान्य कारक को कोष्ठक से निकाल दिया जाता है। प्रत्येक कारक शून्य के बराबर है, जो आपको समीकरण की जड़ों को निर्धारित करने की अनुमति देता है। फिर दिए गए खंड से संबंधित जड़ों को घुमावों की विधि द्वारा निर्धारित किया जाता है। ऐसा करने के लिए, निर्दिष्ट खंड की बाईं सीमा से दाईं ओर निर्मित इकाई सर्कल पर एक लूप चिह्नित किया गया है। इसके अलावा, यूनिट सर्कल पर पाए गए जड़ों को इसके केंद्र के साथ खंडों से जोड़ा जाता है और जिन बिंदुओं पर ये खंड लूप को काटते हैं, उन्हें निर्धारित किया जाता है। ये प्रतिच्छेदन बिंदु समस्या के दूसरे भाग का वांछित उत्तर हैं।