Šioje pamokoje išmoksime skaičiuoti plokščių figūrų plotas kurie vadinami lenktos trapecijos .
Tokių formų pavyzdžiai pateikti paveikslėlyje žemiau.
Viena vertus, naudojant konkretų integralą, labai lengva rasti plokščios figūros plotą. Mes kalbame apie figūros plotą, kurį iš viršaus riboja tam tikra kreivė, iš apačios - abscisių ašimi ( Jautis) ir kelios tiesios linijos į kairę ir į dešinę. Paprastumas yra tas funkcijos, kuriai pateikta kreivė, apibrėžtasis integralas yra tokios figūros plotas(lenkta trapecija).
Norėdami apskaičiuoti figūros plotą, mums reikia:
- Funkcijos, apibrėžiančios kreivę, apibrėžtasis integralas , kuri iš viršaus riboja lenktą trapeciją. Ir čia iškyla pirmasis reikšmingas niuansas: lenkta trapecija gali būti apribota kreive ne tik iš viršaus, bet ir iš apačios ... Kaip elgtis tokiu atveju? Paprasta, bet svarbu atsiminti: integralas šiuo atveju imamas su minuso ženklu .
- Integracijos ribos a ir b, kurią randame iš linijų, jungiančių figūrą į kairę ir į dešinę, lygčių: x = a , x = b, kur a ir b- skaičiai.
Atskirai apie dar keletą niuansų.
Kreivė, kuri riboja išlenktą trapeciją aukščiau (arba žemiau), turi būti tolydžios ir neneigiamos funkcijos grafikas y = f(x) .
X reikšmės turi priklausyti linijos segmentui [a, b]. Tai yra, neatsižvelgiama į tokias, pavyzdžiui, linijas kaip grybo pjūvis, kuriose koja gerai telpa į šį segmentą, o kepurė yra daug platesnė.
Šoniniai segmentai gali išsigimti į taškus ... Jei brėžinyje matote tokią figūrą, tai neturėtų jūsų suklaidinti, nes šis taškas visada turi savo reikšmę x ašyje. Tai reiškia, kad viskas tvarkoje su integracijos ribomis.
Dabar galite pereiti prie formulių ir skaičiavimų. Taigi sritis s kreivinę trapeciją galima apskaičiuoti pagal formulę
Jeigu f(x) ≤ 0 (funkcijos grafikas yra žemiau ašies Jautis), tada išlenktas trapecijos plotas galima apskaičiuoti pagal formulę
Taip pat pasitaiko atvejų, kai ir viršutinė, ir apatinė figūros ribos yra atitinkamai funkcijos. y = f(x) ir y = φ (x) , tada tokios figūros plotas apskaičiuojamas pagal formulę
![]() . (3)
. (3)
Problemas sprendžiame kartu
Pradėkime nuo atvejų, kai figūros plotą galima apskaičiuoti naudojant formulę (1).
1 pavyzdys.Jautis) ir tiesiomis linijomis x = 1 , x = 3 .

Sprendimas. Nes y = 1/x> 0 atkarpoje, tada kreivinės trapecijos plotas randamas pagal formulę (1):
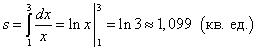 .
.
2 pavyzdys. Raskite figūros plotą, kurį riboja funkcijos grafikas, tiesė x= 1 ir abscisė ( Jautis ).

Sprendimas. (1) formulės taikymo rezultatas:
![]()
Jei tada s= 1/2; jei tada s= 1/3 ir kt.
3 pavyzdys. Raskite figūros plotą, kurį riboja funkcijos grafikas, abscisių ašis ( Jautis) ir tiesioginis x = 4 .

Sprendimas. Uždavinio sąlygą atitinkanti figūra yra kreivinė trapecija, kurioje kairioji atkarpa išsigimusi į tašką. Integravimo ribos yra 0 ir 4. Kadangi pagal (1) formulę randame kreivinės trapecijos plotą:
 .
.
4 pavyzdys. Raskite figūros plotą, kurį riboja linijos ir kuri yra 1 ketvirtyje.

Sprendimas. Norėdami naudoti formulę (1), figūros plotą, nurodytą pavyzdžio sąlygomis, pavaizduojame kaip trikampio plotų sumą OAB ir lenkta trapecija ABC... Skaičiuojant trikampio plotą OAB integracijos ribos yra taškų abscisės O ir A, ir figūrai ABC- taškų abscisės A ir C (A yra linijos sankirta OA ir parabolės, ir C- parabolės susikirtimo su ašimi taškas Jautis). Kartu (kaip sistemą) išsprendę tiesės ir parabolės lygtis, gauname (taško abscisę A) ir (kito tiesės ir parabolės susikirtimo taško abscisė, kuri nereikalinga sprendiniui). Panašiai gauname (taškų abscises C ir D). Dabar turime viską, kad rastume figūros plotą. Mes randame:

5 pavyzdys. Raskite lenktos trapecijos plotą ACDB jei kreivės lygtis CD ir abscisės A ir B atitinkamai 1 ir 2.

Sprendimas. Išreikškime šią kreivės lygtį žaidimo prasme: Kreivės trapecijos plotas randamas pagal formulę (1):
 .
.
Mes kreipiamės į atvejus, kai figūros plotą galima apskaičiuoti pagal (2) formulę.
6 pavyzdys. Raskite figūros plotą, kurį riboja parabolė ir abscisių ašis ( Jautis ).

Sprendimas. Šis skaičius yra žemiau abscisių ašies. Todėl jo plotui apskaičiuoti naudosime (2) formulę. Integravimo ribos yra abscisės ir parabolės susikirtimo su ašimi taškai Jautis... Vadinasi,

7 pavyzdys. Raskite plotą, esantį tarp abscisių ašies ( Jautis) ir dvi gretimos sinusinės bangos.

Sprendimas. Šios figūros plotą galima rasti pagal formulę (2):
![]() .
.
Raskime kiekvieną terminą atskirai:
 .
.
 .
.
Galiausiai randame sritį:
![]() .
.
8 pavyzdys. Raskite figūros, esančios tarp parabolės ir kreivės, plotą.

Sprendimas. Išreikškime linijų lygtis žaidimo prasme:
Plotas pagal (2) formulę gaunamas kaip
![]() ,
,
kur a ir b- taškų abscisės A ir B... Juos randame kartu išspręsdami lygtis:

Galiausiai randame sritį:

Ir galiausiai atvejai, kai figūros plotą galima apskaičiuoti pagal (3) formulę.
9 pavyzdys. Raskite figūros, esančios tarp parabolių, plotą ![]() ir .
ir .
NASA pradės ekspediciją į Marsą 2020 m. liepos mėn. Erdvėlaivis į Marsą pristatys elektroninį nešiklį su visų registruotų ekspedicijos narių pavardėmis.
Jei šis įrašas išsprendė jūsų problemą arba jums jis tiesiog patiko, pasidalykite nuoroda į jį su draugais socialiniuose tinkluose.
Vienas iš šių kodo variantų turi būti nukopijuotas ir įklijuotas į jūsų tinklalapio kodą, geriausia tarp žymų
ir arba iškart po žymos ... Pagal pirmąjį variantą MathJax įkeliamas greičiau ir mažiau sulėtina puslapį. Tačiau antroji parinktis automatiškai seka ir įkelia naujausias MathJax versijas. Jei įterpsite pirmąjį kodą, jį reikės periodiškai atnaujinti. Jei įterpsite antrą kodą, puslapiai bus įkeliami lėčiau, tačiau jums nereikės nuolat stebėti MathJax atnaujinimų.Lengviausias būdas prijungti „MathJax“ yra „Blogger“ arba „WordPress“: savo svetainės prietaisų skydelyje pridėkite valdiklį, skirtą trečiosios šalies „JavaScript“ kodui įterpti, nukopijuokite į jį pirmąją arba antrąją anksčiau pateikto įkėlimo kodo versiją ir įdėkite valdiklį arčiau šablono pradžia (beje, tai visai nebūtina, nes MathJax scenarijus įkeliamas asinchroniškai). Tai viskas. Dabar išmokite MathML, LaTeX ir ASCIIMathML žymėjimo sintaksę ir būsite pasiruošę į savo svetainės tinklalapius įterpti matematines formules.
Dar viena Naujųjų metų išvakarės... šaltas oras ir snaigės ant lango stiklo... Visa tai paskatino mane vėl parašyti apie... fraktalus ir ką apie tai žino Volframas Alfa. Apie tai yra įdomus straipsnis, kuriame pateikiami dvimačių fraktalų struktūrų pavyzdžiai. Čia apžvelgsime sudėtingesnius 3D fraktalų pavyzdžius.
Fraktalą galima vizualizuoti (apibūdinti) kaip geometrinę figūrą arba kūną (tai reiškia, kad abu yra rinkinys, šiuo atveju taškų rinkinys), kurių detalės turi tokią pačią formą kaip ir pati pirminė figūra. Tai yra, tai yra į save panaši struktūra, kurios detales įvertinus padidinus matysime tokią pat formą kaip ir be padidinimo. Tuo tarpu taisyklingos geometrinės figūros (ne fraktalo) atveju, kai priartinsime, pamatysime detales, kurių forma yra paprastesnė nei pati pradinė forma. Pavyzdžiui, esant pakankamai dideliam padidinimui, dalis elipsės atrodo kaip linijos atkarpa. Taip neatsitinka su fraktalais: esant bet kokiam padidėjimui, mes vėl pamatysime tą pačią sudėtingą formą, kuri kartosis vėl ir vėl su kiekvienu padidėjimu.
Fraktalų mokslo įkūrėjas Benoit Mandelbrot savo straipsnyje Fraktalai ir menas mokslui rašė: „Fraktalai yra geometrinės figūros, kurių detalės yra tokios pat sudėtingos, kaip ir bendra forma. Dalis fraktalų bus padidinta iki visa tai atrodys kaip visuma arba tiksliai, o gal su nedidele deformacija.
Integruotas pritaikymas taikomųjų problemų sprendimui
Skaičiuojant plotą
Tolydžios neneigiamos funkcijos f (x) apibrėžtasis integralas skaitiniu požiūriu lygus kreivės trapecijos plotas, apribotas kreivės y = f (x), ašies O x ir tiesių x = a ir x = b. Atitinkamai, ploto formulė parašyta taip:
Pažvelkime į keletą plokščių figūrų plotų skaičiavimo pavyzdžių.
Uždavinys Nr.1. Apskaičiuokite plotą, kurį riboja tiesės y = x 2 +1, y = 0, x = 0, x = 2.
Sprendimas. Sukurkime figūrą, kurios plotą turėsime apskaičiuoti.
 y = x 2 + 1 yra parabolė, kurios šakos nukreiptos į viršų, o parabolė O y ašies atžvilgiu pasislinkusi vienu vienetu aukštyn (1 pav.).
y = x 2 + 1 yra parabolė, kurios šakos nukreiptos į viršų, o parabolė O y ašies atžvilgiu pasislinkusi vienu vienetu aukštyn (1 pav.).
1 pav. Funkcijos y = x 2 + 1 grafikas
Uždavinio numeris 2. Apskaičiuokite plotą, kurį riboja tiesės y = x 2 - 1, y = 0 intervale nuo 0 iki 1.
 |
Sprendimas.Šios funkcijos grafikas yra šakos parabolė, kuri nukreipta į viršų, o parabolė O y ašies atžvilgiu pasislenka vienu vienetu žemyn (2 pav.).
2 pav. Funkcijos y = x 2 - 1 grafikas
Uždavinio numeris 3. Padarykite brėžinį ir apskaičiuokite figūros, apribotos linijomis, plotą
y = 8 + 2x - x 2 ir y = 2x - 4.
Sprendimas. Pirmoji iš šių dviejų tiesių yra parabolė su šakomis, nukreiptomis žemyn, nes koeficientas x 2 yra neigiamas, o antroji linija yra tiesė, kertanti abi koordinačių ašis.
Norėdami sukurti parabolę, randame jos viršūnės koordinates: y ’= 2 - 2x; 2 - 2x = 0, x = 1 - viršūnės abscisė; y (1) = 8 + 2 ∙ 1 - 1 2 = 9 yra jo ordinatė, N (1; 9) yra viršūnė.
Dabar rasime parabolės ir tiesės susikirtimo taškus, išspręsdami lygčių sistemą:

Lygties dešiniųjų kraštinių prilyginimas, kurių kairiosios pusės lygios.
Gauname 8 + 2x - x 2 = 2x - 4 arba x 2 - 12 = 0, iš kur ![]() .
.
Taigi taškai yra parabolės ir tiesės susikirtimo taškai (1 pav.).


3 pav. Funkcijų y = 8 + 2x - x 2 ir y = 2x - 4 grafikai
Sukonstruokime tiesę y = 2x - 4. Ji eina per taškus (0; -4), (2; 0) koordinačių ašyse.
Norėdami sukurti parabolę, taip pat galite turėti jos susikirtimo taškus su 0x ašimi, ty lygties šaknis 8 + 2x - x 2 = 0 arba x 2 - 2x - 8 = 0. Pagal Vietos teoremą tai lengva rasti jo šaknis: x 1 = 2, x 2 = 4.
3 paveiksle parodyta figūra (parabolinė atkarpa M 1 N M 2), apribota šiomis linijomis.
Antroji užduoties dalis – rasti šios figūros plotą. Jo plotą galima rasti naudojant apibrėžtąjį integralą pagal formulę  .
.
Atsižvelgdami į šią sąlygą, gauname integralą: 
2 Apsisukimo kūno tūrio apskaičiavimas
Kūno tūris, gautas sukant kreivę y = f (x) aplink O x ašį, apskaičiuojamas pagal formulę:
Sukant aplink O y ašį formulė atrodo taip:
Problema numeris 4. Nustatykite kūno tūrį, gautą sukant lenktą trapeciją, ribojamą tiesių x = 0 x = 3 ir kreivės y = aplink O x ašį.
Sprendimas. Pastatykime paveikslėlį (4 pav.).

4 pav. Funkcijos y = grafikas
Reikalingas tūris yra 
Problema numeris 5. Apskaičiuokite kūno tūrį, gautą sukant lenktą trapeciją, kurią riboja kreivė y = x 2 ir tiesės y = 0 ir y = 4 aplink O y ašį.
Sprendimas. Mes turime:

Peržiūrėkite klausimus
Apsvarstykite kreivąją trapeciją, kurią riboja Ox ašis, kreivė y = f (x) ir dvi tiesės: x = a ir x = b (85 pav.). Paimkime savavališką x reikšmę (bet ne a ir ne b). Suteikime jam prieaugį h = dx ir panagrinėkime juostą, ribojamą tiesių AB ir CD, Ox ašies ir lanko BD, priklausančių nagrinėjamai kreivei. Ši juostelė bus vadinama elementaria juostele. Elementariosios juostelės plotas nuo stačiakampio ACQB ploto skiriasi lenktu trikampiu BQD, o pastarojo plotas yra mažesnis už stačiakampio BQDM, kurio kraštinės BQ = h = dx, plotą. ) QD = Ay ir plotas, lygus hay = Ay dx. Mažėjant pusei h, pusė Du taip pat mažėja ir kartu su h linksta į nulį. Todėl BQDM plotas yra antros eilės be galo mažas. Elementariosios juostos plotas yra ploto prieaugis, o stačiakampio ACQB plotas, lygus AB-AC == / (x) dx>, yra ploto skirtumas. Todėl pačią sritį randame integruodami jos skirtumą. Nagrinėjamoje figūroje nepriklausomas kintamasis l: kinta nuo a iki b, todėl reikalingas plotas 5 bus lygus 5 = \ f (x) dx. (I) 1 pavyzdys. Apskaičiuokime plotą, kurį riboja parabolė y - 1 -x *, tiesės X = - Fj-, x = 1 ir ašis O * (86 pav.). pav. 87. pav. 86. 1 Čia f (x) = 1 - n?, integravimo ribos yra a = - ir t = 1, todėl 3) | _ 2 3V 2 / J 3 24 24 * 2 pavyzdys. Apskaičiuokite plotą, kurį riboja sinusoidė y = sinXy pagal Ox ašį ir tiesę (87 pav.). Taikydami formulę (I) gauname Л 2 S = J sinxdx = [-cos x] Q = 0 - (- 1) = lf 3 pavyzdys. Apskaičiuokite plotą, kurį riboja sinusoidės lankas ^ y = sin jc, uždarytas tarp dviejų gretimų susikirtimo su Ox ašimi taškų (pavyzdžiui, tarp pradžios ir taško su abscise i). Atkreipkite dėmesį, kad iš geometrinių svarstymų aišku, kad ši sritis bus dvigubai didesnė už ankstesnio pavyzdžio plotą. Tačiau atlikime skaičiavimus: i 5 = | s \ nxdx = [- cosx) * - - cos i - (- cos 0) = 1 + 1 = 2. o Iš tiesų, mūsų prielaida pasirodė teisinga. 4 pavyzdys Apskaičiuokite plotą, apribotą sinusoidės ir ^ Ox ašies per vieną periodą (88 pav.). Preliminarūs svarstymai leidžia daryti prielaidą, kad plotas bus keturis kartus didesnis nei pr. 2. Tačiau atlikus skaičiavimus gauname "i G, * i S - \ sin x dx = [- cos x] 0 = = - cos 2l - (- cos 0) = - 1 + 1 = 0. Šį rezultatą reikia patikslinti. Siekdami išsiaiškinti reikalo esmę, taip pat apskaičiuojame plotą, kurį riboja ta pati sinusoidė y = sin l: ir Ox ašis intervale nuo l iki 2i. Taikant (I) formulę, gauname 2l $ 2l sin xdx = [- cosx] l = -cos 2ya ~) -c05ya = - 1-1 = -2. Taigi matome, kad ši sritis pasirodė neigiama. Palyginus jį su plotu, apskaičiuotu 3 pr., matome, kad jų absoliučios reikšmės yra vienodos, tačiau skiriasi ženklai. Jei pritaikysime savybę V (žr. XI skyrių, § 4), tai gausime 2l I 2l J sin xdx = J sin * dx [sin x dx = 2 + (- 2) = 0 Tai, kas atsitiko šiame pavyzdyje, nėra atsitiktinai. . Visada plotas žemiau Ox ašies, jei nepriklausomas kintamasis keičiasi iš kairės į dešinę, gaunamas skaičiuojant neigiamus integralus. Šiame kurse visada atsižvelgsime į nepažymėtus kvadratus. Todėl ką tik analizuotame pavyzdyje atsakymas bus toks: reikalingas plotas lygus 2 + | -2 | = 4. 5 pavyzdys. Apskaičiuokime OAB plotą, parodytą fig. 89. Šią sritį riboja Ox ašis, parabolė y = - xr ir tiesė y - = -x + \. Kreivinė trapecijos sritis Paieškos sritis OAV susideda iš dviejų dalių: OAM ir MAV. Kadangi taškas A yra parabolės ir tiesės susikirtimo taškas, jo koordinates rasime išsprendę lygčių sistemą 3 2 Y = mx. (reikia rasti tik taško A abscisę). Išspręsdami sistemą, randame l; = ~. Todėl plotas turi būti skaičiuojamas dalimis, pirmasis kvadratas. OAM ir tada pl. MAV: .... G 3 2, 3 G xP 3 1/2 U 2. Qam- ^ x)

































