La droite y = 3x + 2 est tangente au graphique de la fonction y = -12x ^ 2 + bx-10. Trouvez b, étant donné que l'abscisse du point de contact est inférieure à zéro.

Afficher la solution

Solution

Soit x_0 l'abscisse du point sur le graphique de la fonction y = -12x ^ 2 + bx-10, par lequel passe la tangente à ce graphique.

La valeur de la dérivée au point x_0 est égale à la pente de la tangente, c'est-à-dire y "(x_0) = - 24x_0 + b = 3. Par contre, le point tangent appartient à la fois au graphe de la fonction et la tangente, c'est-à-dire -12x_0 ^ 2 + bx_0-10 = 3x_0 + 2. On obtient le système d'équations \ begin (cas) -24x_0 + b = 3, \\ - 12x_0 ^ 2 + bx_0-10 = 3x_0 + 2. \ fin (cas)

En résolvant ce système, nous obtenons x_0 ^ 2 = 1, ce qui signifie soit x_0 = -1, soit x_0 = 1. Selon la condition, l'abscisse du point de contact est inférieure à zéro, donc x_0 = -1, puis b = 3 + 24x_0 = -21.

Réponse

État

La figure montre le graphique de la fonction y = f (x) (qui est une ligne brisée composée de trois segments de ligne droite). À l'aide de la figure, calculez F (9) -F (5), où F (x) est l'une des primitives de f (x).

Afficher la solution

Solution

D'après la formule de Newton-Leibniz, la différence F (9) -F (5), où F (x) est une des primitives de la fonction f (x), est égale à l'aire du trapèze curviligne borné par le graphique de la fonction y = f (x), par les droites y = 0 , x = 9 et x = 5. D'après le graphique, nous déterminons que le trapèze courbe indiqué est un trapèze avec des bases égales à 4 et 3 et une hauteur de 3.

Sa superficie est \ frac (4 + 3) (2) \ cdot 3 = 10,5.

Réponse

Source : « Mathématiques. Préparation à l'examen-2017. Niveau de profil ". Éd. FF Lyssenko, S. Yu. Kulabukhova.

État

La figure montre le graphique de y = f "(x) - la dérivée de la fonction f (x), définie sur l'intervalle (-4; 10). Trouvez les intervalles de diminution de la fonction f (x). Dans le réponse, indiquez la longueur du plus grand d'entre eux.

Afficher la solution

Solution

Comme vous le savez, la fonction f (x) décroît sur ces intervalles, en chaque point desquels la dérivée f "(x) est inférieure à zéro. Compte tenu du fait qu'il est nécessaire de trouver la longueur du plus grand d'entre eux, trois de tels intervalles se distinguent naturellement du chiffre : (-4 ; -2) ; (0 ; 3) ; (5 ; 9).

La longueur du plus grand d'entre eux - (5; 9) est égale à 4.

Réponse

Source : « Mathématiques. Préparation à l'examen-2017. Niveau de profil ". Éd. FF Lyssenko, S. Yu. Kulabukhova.

État

La figure montre le graphique de y = f "(x) - la dérivée de la fonction f (x), définie sur l'intervalle (-8; 7). Trouvez le nombre de points maximum de la fonction f (x) appartenant à l'intervalle [-6; -2].

Afficher la solution

Solution

Le graphique montre que la dérivée f "(x) de la fonction f (x) change de signe de plus en moins (c'est à de tels points qu'il y aura un maximum) à exactement un point (entre -5 et -4) de l'intervalle [-6; -2 ]. Par conséquent, il y a exactement un point maximum sur l'intervalle [-6; -2].

Réponse

Source : « Mathématiques. Préparation à l'examen-2017. Niveau de profil ". Éd. FF Lyssenko, S. Yu. Kulabukhova.

État

La figure montre le graphe de la fonction y = f (x), définie sur l'intervalle (-2 ; 8). Déterminer le nombre de points auxquels la dérivée de la fonction f (x) est 0.

Afficher la solution

Solution

L'égalité à zéro de la dérivée en un point signifie que la tangente au graphe de la fonction, tracée en ce point, est parallèle à l'axe Ox. Par conséquent, nous trouvons des points auxquels la tangente au graphique de la fonction est parallèle à l'axe Ox. Sur ce graphique, ces points sont des points extrêmes (points de maximum ou de minimum). Comme vous pouvez le voir, il y a 5 points extremum.

Réponse

Source : « Mathématiques. Préparation à l'examen-2017. Niveau de profil ". Éd. FF Lyssenko, S. Yu. Kulabukhova.

État

La droite y = -3x + 4 est parallèle à la tangente au graphique de la fonction y = -x ^ 2 + 5x-7. Trouvez l'abscisse du point de contact.

Afficher la solution

Solution

La pente de la droite vers le graphique de la fonction y = -x ^ 2 + 5x-7 en un point arbitraire x_0 est égale à y "(x_0). Mais y" = - 2x + 5, donc y "(x_0 ) = - 2x_0 + 5. Angulaire le coefficient de la droite y = -3x + 4 spécifié dans la condition est égal à -3. Les droites parallèles ont la même pente. On trouve donc la valeur x_0 telle que = -2x_0 + 5 = -3.

On obtient : x_0 = 4.

Réponse

Source : « Mathématiques. Préparation à l'examen-2017. Niveau de profil ". Éd. FF Lyssenko, S. Yu. Kulabukhova.

État

La figure montre le graphique de la fonction y = f (x) et les points -6, -1, 1, 4 sont marqués sur l'axe des abscisses. Auquel de ces points la valeur de la dérivée est-elle la plus petite ? Indiquez ce point dans votre réponse.

Classe de maître en mathématiques

en 11e année

sur ce sujet

" FONCTION DÉRIVÉE

DANS LES TÂCHES DE L'UTILISATION "

professeur de mathématiques

Martynenko E.N.

Année académique 2017-2018

Le but du master - classe: développer les compétences des élèvesapplication des connaissances théoriques sur le thème "Dérivé de la fonction" pour résoudre les problèmes de l'examen d'État unifié.

Tâches

Éducatif:résumer et systématiser les connaissances des étudiants sur le sujet

"Dérivé d'une fonction", considérez les prototypes des problèmes USE sur ce sujet, offrez aux étudiants l'opportunité de tester leurs connaissances lors de la résolution de problèmes par eux-mêmes.

Développement: promouvoir le développement de la mémoire, de l'attention, de l'estime de soi et de la maîtrise de soi; la formation de compétences clés de base (comparaison, juxtaposition, classification d'objets, détermination de moyens adéquats pour résoudre un problème éducatif sur la base des algorithmes donnés, la capacité d'agir de manière autonome dans une situation d'incertitude, de contrôler et d'évaluer leurs activités, de trouver et éliminer les causes des difficultés apparues).

Éducatif: promouvoir:

Formation d'une attitude responsable envers l'apprentissage chez les étudiants ;

développer un intérêt soutenu pour les mathématiques;

créer une motivation intrinsèque positive pour étudier les mathématiques.

Les technologies : apprentissage individualisé différencié, TIC.

Méthodes d'enseignement : verbal, visuel, pratique, problématique.

Formes de travail : individuel, frontal, par paires.

Matériel et matériel pour le cours :projecteur, écran, PC, simulateur(Annexe 1), présentation pour le cours(Annexe 2), individuellement - cartes différenciées pour un travail indépendant en binôme(Annexe n°3), liste de sites Internet, devoirs différenciés individuellement(Annexe #4).

Explication pour la classe de maître.

Cette classe de maître a lieu en 11e année pour préparer l'examen d'État unifié. Vise l'application du matériel théorique sur le thème "Dérivé d'une fonction" dans la résolution de problèmes d'examen.

Durée de la master class- 20 minutes.

Structure de classe de maître

I. Moment d'organisation -1 min.

II.Communication du sujet, objectifs du master - classe, motivation des activités pédagogiques - 1 min.

III. Travail frontal. Formation "Tâches n°14 BASE, n°7 PROFIL de l'examen d'État unifié". Analyse du travail avec le simulateur - 7 min.

IV.Individuellement - Travail différencié en binôme. Solution indépendante des problèmes n° 12. (PROFIL) Contrôle mutuel - 9 min. Tests en ligne (BASE) Analyse des résultats des tests - 8 min

V. Vérification des devoirs individuels. -1 minute.

Vi. Individuel - devoirs différenciés -1 min.

VII. TEST DE CONTRLE 20 MINUTES (4 OPTIONS)

Progression de la classe de maître

je .Temps d'organisation.

II Communication du sujet, objectifs de la master-class, motivation des activités pédagogiques.

(Diapositives 1-2, Annexe #2)

Le sujet de notre leçon est "La dérivée d'une fonction dans les tâches de l'examen". Tout le monde connaît le dicton « Petite bobine mais chère ». L'une de ces « bobines » en mathématiques est la dérivée. Le dérivé est utilisé pour résoudre de nombreux problèmes pratiques en mathématiques, physique, chimie, économie et autres disciplines. Il vous permet de résoudre des problèmes simplement, magnifiquement et de manière intéressante.

Le sujet "Dérivé" est présenté dans la tâche n ° 14 du niveau de base et dans les tâches du niveau de profil n ° 7,12, 18 et l'examen d'état unifié.

Vous avez travaillé avec des documents réglementant la structure et le contenu des matériaux de mesure de contrôle de l'examen d'État unifié en mathématiques 2018. Tirez une conclusion sur les connaissances et les compétences dont vous avez besoin pour résoudre avec succès les problèmes USE sur le thème "Dérivé".

(Diapositives 3-4, Annexe #2)

Avez-vous appris "Codificateur des éléments de contenu en MATHÉMATIQUES pour la préparation des matériels de mesure de contrôle pour l'examen d'État unifié",

"Codificateur des exigences pour le niveau de formation des diplômés", "Spécification des matériaux de mesure de contrôle", "Version de démonstration des matériaux de mesure de contrôle de l'examen d'État unifié 2018" et découvert quelles connaissances et compétences sur la fonction et sa dérivée sont nécessaires pour résoudre avec succès des problèmes sur le thème "Dérivée".

Nécessaire

• CONNAÎTRE

règles de calcul des dérivés ;

dérivées de fonctions élémentaires de base;

la signification géométrique et physique de la dérivée ;
équation de la tangente au graphe de la fonction ;
étude d'une fonction à l'aide d'une dérivée.

• ÊTRE CAPABLE DE

effectuer des actions avec des fonctions (décrire le comportement et les propriétés d'une fonction selon le graphique, trouver ses valeurs les plus élevées et les plus basses).

• UTILISER

acquis des connaissances et des compétences dans la pratique et la vie quotidienne.

Vous avez des connaissances théoriques sur le sujet Dérivés. Aujourd'hui, nous allonsAPPRENDRE À APPLIQUER LES CONNAISSANCES SUR LA FONCTION DÉRIVÉE POUR RÉSOUDRE LES PROBLÈMES D'UTILISATION.(Diapositive 4, annexe n° 2)

ce n'est pas pour rien Aristote a dit que"L'ESPRIT N'EST PAS SEULEMENT DANS LA CONNAISSANCE, MAIS AUSSI DANS LA CAPACITÉ D'APPLIQUER LA CONNAISSANCE DANS LA PRATIQUE"(Diapositive 5, annexe n° 2)

A la fin de la leçon, nous reviendrons sur le but de notre leçon et découvrirons si nous l'avons atteint ?

III ... Travail frontal.Formation "Tâches n°14 BASE n°7 PROFIL de l'examen d'État unifié" ( Annexe n° 1). Analyse du travail avec le simulateur.

Choisissez la bonne réponse parmi les quatre proposées.

Quelle est, selon vous, la difficulté d'accomplir la tâche n°7 ?

Que pensez-vous, quelles sont les erreurs typiques que font les diplômés à l'examen lorsqu'ils résolvent ce problème ?

En répondant aux questions de la tâche n ° 14 BASE ET n ° 7 PROFIL, vous devez être capable de décrire le comportement et les propriétés de la fonction à partir du graphique de la dérivée et à partir du graphique de la fonction - le comportement et les propriétés de la dérivée de la fonction. Et cela nécessite de bonnes connaissances théoriques sur les sujets suivants : « Signification géométrique et mécanique de la dérivée. Tangente au graphe de la fonction. Application de la dérivée à l'étude des fonctions ».

Analysez quelles tâches vous ont causé des difficultés?

Quelles questions théoriques avez-vous besoin de savoir?

IV. Оn - test en ligne sur les affectations №14 (BASE)Analyse des résultats des tests.

Site pour tester dans la leçon:http://www.mathb-ege.sdamgia.ru/

Qui n'a pas fait d'erreurs ?

Qui a eu des difficultés à tester ? Pourquoi?

Dans quelles tâches des erreurs ont-elles été commises ?

Pour conclure, quelles questions théoriques avez-vous besoin de savoir ?

Individuellement - travail différencié en binôme. La solution indépendante des problèmes №12. (PROFIL)Vérification mutuelle.(Annexe #3)

Rappelez-vous l'algorithme de résolution des problèmes №12 de l'examen pour trouver des points extremum, des extrema d'une fonction, les valeurs les plus grandes et les plus petites d'une fonction sur l'intervalle en utilisant la dérivée.

Résoudre des problèmes avec une dérivée

Les élèves sont confrontés à un problème :

« Pensez-vous, est-il possible de résoudre certains problèmes n°12 d'une manière différente, sans utiliser de dérivée ? »

1 paire

2 paires

3 paires

4 paires

(Les élèves défendent leur solution en écrivant les principales étapes de la résolution de problèmes au tableau. Les élèves proposent deux façons de résoudre le problème n° 2).

Résolution d'un problème. Conclusion pour les étudiants :

"Certains problèmes n°12 de l'examen pour trouver la plus petite et la plus grande valeur d'une fonction peuvent être résolus sans utiliser la dérivée, en s'appuyant sur les propriétés des fonctions."

Analysez quelle erreur vous avez commise dans la tâche ?

Quelles questions théoriques devez-vous répéter?

V. Vérification des devoirs individuels. (Diapositives 7-8, annexe n° 2)

Vegelman V. a reçu des devoirs individuels: à partir des manuels de préparation à l'examen numéro 18.

(L'étudiant donne la solution du problème, en s'appuyant sur la méthode fonctionnelle-graphique, comme l'une des méthodes de résolution du problème n°18 de l'examen et donne une brève explication de cette méthode).

VII. Individuel - devoirs différenciés

(Diapositive 9, annexe n° 2), (Annexe #4).

J'ai préparé une liste de sites Internet pour préparer l'examen. Vous pouvez également passer des tests en ligne sur ces sites. Pour la leçon suivante, vous devez : 1) revoir le matériel théorique sur le thème « Dérivé d'une fonction » ;

2) sur le site "Banque ouverte de tâches en mathématiques" (http://mathege.ru/ ) trouver des prototypes des tâches N°14 BASE ET N°7 et 12 PROFIL et résoudre au moins 10 problèmes PROFIL ;

3) V. Vegelman, résoudre des problèmes avec paramètres (ANNEXE 4). tâches 1-8 (option 1).UN NIVEAU DE BASE DE

VIII. Notes de cours.

Comment vous évalueriez-vous pour une leçon ?

Pensez-vous que vous auriez pu faire mieux dans la leçon?

IX. Résumé de la leçon. Réflexion

Résumons notre travail. Quel était le but de la leçon ? Pensez-vous qu'il a été atteint?

Regardez le tableau et dans une phrase, en choisissant le début de la phrase, continuez avec la phrase qui vous convient le mieux.

J'ai senti…

J'ai appris…

Je me suis débrouillé …

J'étais capable de ...

J'essaierai …

J'ai été surpris que …

Je voulais…

Pouvez-vous dire qu'au cours de la leçon il y a eu un enrichissement de votre stock de connaissances ?

Ainsi, vous avez répété les questions théoriques sur la dérivée de la fonction, appliqué vos connaissances à la résolution des prototypes des tâches USE (N° 14 NIVEAU DE BASE N° 7,12 NIVEAU DE PROFIL), et V. Vegelman a terminé la tâche n° 18 avec un paramètre, ce qui est une tâche d'un degré accru de difficultés.

Ce fut un plaisir pour moi de travailler avec vous, et j'espère que vous pourrez appliquer avec succès les connaissances acquises dans les cours de mathématiques non seulement lors de la réussite de l'examen, mais également dans vos études ultérieures.

Je voudrais terminer la leçon avec les mots d'un philosophe italienThomas d'Aquin"La connaissance est une chose si précieuse qu'il n'est pas honteux de l'obtenir de n'importe quelle source."(Diapositive 10, Annexe #2).

Je te souhaite de réussir ta préparation à l'examen !

Aperçu:

Pour utiliser l'aperçu des présentations, créez vous-même un compte Google (compte) et connectez-vous : https://accounts.google.com

Légendes des diapositives :

Préparation à l'examen SIMULATEUR sur le thème "Dérivé" Tâche numéro 14 niveau de base, numéro 7, niveau 12 profil

f (x) f / (x) x La figure montre le graphique de la dérivée de la fonction y = f (x), spécifiée sur l'intervalle (- 8 ; 8). Explorons les propriétés du graphe et nous pourrons répondre à de nombreuses questions sur les propriétés de la fonction, bien que le graphe de la fonction elle-même ne soit pas présenté ! y = f / (x) 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 4 3 2 1 -1 -2 -3 -4 -5 yx 6 3 0 -5 Trouver des points où f / (x) = 0 (ce sont les zéros de la fonction). + - - + +

DEVOIR numéro 14 Mathématiques niveau de base

La figure montre le graphique de la fonction y = f (x) et les points A, B, C et D sont marqués sur l'axe Ox. A l'aide du graphe, attribuez à chaque point les caractéristiques de la fonction et de sa dérivée. ABCD 1) la valeur de la fonction au point est négative et la valeur de la dérivée de la fonction au point est positive 2) la valeur de la fonction au point est positive et la valeur de la dérivée de la fonction au point est négative 3) la valeur de la fonction au point est négative, et la valeur de la dérivée de la fonction au point est négative 4) la valeur de la fonction au point est positive, et la valeur de la la dérivée de la fonction au point est positive

№ 1 La figure montre le graphique de la fonction y = f (x) et les points marqués A, B, C et D sur l'axe Ox. A l'aide du graphe, attribuez à chaque point les caractéristiques de la fonction et de sa dérivée. 1) la valeur de la fonction au point est positive, et la valeur de la dérivée de la fonction au point est négative 2) la valeur de la fonction au point est négative, et la valeur de la dérivée de la fonction au le point est négatif 3) la valeur de la fonction au point est positive et la valeur de la dérivée de la fonction au point est positive 4) la valeur de la fonction au point est négative et la valeur de la dérivée de la fonction au point est positif ABCD

La figure montre le graphique de la fonction y = f (x). Les points a, b, c, d et e définissent des intervalles sur l'axe Ox. A l'aide du graphe, attribuez à chaque intervalle la caractéristique de la fonction ou sa dérivée. A) (a; b) B) (b; c) C) (c; d) D) (d; e) 1) les valeurs de la fonction sont positives en chaque point de l'intervalle 2) les valeurs ​​de la dérivée de la fonction sont négatives en chaque point de l'intervalle 3) les valeurs dérivées de la fonction sont positives en chaque point de l'intervalle 4) les valeurs de la fonction sont négatives en chaque point de l'intervalle

La figure montre le graphique de la fonction y = f (x). Les nombres a, b, c, d et e définissent les intervalles sur l'axe Ox. A l'aide du graphe, attribuez à chaque intervalle la caractéristique de la fonction ou sa dérivée. A) (a; b) B) (b; c) C) (c; d) D) (d; e) 1) les valeurs de la fonction sont positives en chaque point de l'intervalle 2) les valeurs ​​de la fonction sont négatives en chaque point de l'intervalle 3) les valeurs des fonctions dérivées sont négatives en chaque point de l'intervalle 4) les valeurs de la dérivée de la fonction sont positives en chaque point de l'intervalle

La figure montre un graphique d'une fonction et des tangentes qui lui sont tracées aux points avec les abscisses A, B, C et D. A B C D 1) - 1,5 2) 0,5 3) 2 4) - 0,3

La figure montre un graphique d'une fonction et des tangentes qui lui sont tracées aux points avec les abscisses A, B, C et D. A B C D 1) 23 2) - 12 3) - 113 4) 123

DEVOIR numéro 7 Niveau profil Mathématiques

Problèmes pour la signification géométrique de la dérivée

1) La figure montre le graphique de la fonction y = f (x) et sa tangente au point d'abscisse x 0. Trouvez la valeur de la dérivée au point x 0. -2 -0,5 2 0,5 Réfléchissez ! Pense! À droite! Pense! x 0 Signification géométrique de la dérivée : k = tg α L'angle d'inclinaison de la tangente à l'axe Ox est obtus, donc k

5 11 8 2) La fonction continue y = f (x) est réglée sur l'intervalle (-6; 7). La figure montre son graphique. Trouvez le nombre de points auxquels la tangente au graphique de la fonction est parallèle à la droite y = 6. Vérification de y = f (x) y x 3 Réfléchissez ! Pense! Pense! À droite! - 6 7 ans = 6. Point d'arrêt. La dérivée n'existe PAS à ce stade ! -4 3 5 1, 5

Tâches pour déterminer les caractéristiques d'une fonction à partir du graphe de sa dérivée

3) La figure montre le graphique de la dérivée de la fonction y = f / (x), donnée sur l'intervalle (- 6 ; 8). Examinez la fonction y = f (x) pour extremum et indiquez le nombre de ses points extremum. 2 1 4 5 Faux ! Pas vrai! À droite! Pas vrai! Cocher (2) f (x) f / (x) -2 + - y = f / (x) 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 4 3 2 1 - 1 -2 -3 -4 -5 yx -5 + min max О

4 -3 -2 -1 1 2 3 4 5 x 5) La figure montre le graphique de la dérivée d'une fonction spécifiée dans l'intervalle [-5; 5]. Examinez la fonction pour la monotonie et indiquez le point maximum le plus grand. 3 2 4 5 Réfléchissez ! Pense! À droite! Pense! y = f / (x) + + + - - О - f / (x) - + - + - + f (x) -4 -2 0 3 4 Des deux points maximum, le plus grand x max = 3 max max oui

7) La figure montre le graphique de la dérivée de la fonction. Trouvez la longueur de l'intervalle croissant de cette fonction. Cochez O -7 -6 -5 -4 -3 -2 -1 7 6 5 4 3 2 1 -1 -2 -3 -4 -5 -6 -7 4 2 3 5 PENSEZ ! + PENSEZ ! À DROITE! PENSE! y x 3 y = f / (x)

4 -3 -2 -1 1 2 3 4 5 x 6) La figure montre le graphique de la dérivée d'une fonction définie dans l'intervalle [-5; 5]. Examinez la fonction y = f (x) pour la monotonie et indiquez le nombre d'intervalles de diminution. 3 2 4 1 Réfléchissez ! Pense! À droite! Pense! y = f / (x) f (x) -4 -2 0 4 f / (x) - + - + - + + - - - y

Tâches pour déterminer les caractéristiques d'un graphe dérivé d'une fonction.

La figure montre le graphique de la fonction dérivable y = f (x). Neuf points sont marqués en abscisse : x 1, x 2, ..., x 9. Trouvez tous les points marqués auxquels la dérivée de la fonction f (x) est négative. Dans la réponse, indiquez le nombre de ces points.

La figure montre le graphe de la fonction y = f (x), définie sur l'intervalle (a; b). Déterminer le nombre de points entiers auxquels la dérivée de la fonction est positive. a) b) Décidez vous-même ! Solution. s'il augmente. Solutions entières pour : x = -2 ; x = -1 ; x = 5 ; x = 6. Leur nombre est 4. Solutions entières pour : x = 2 ; x = 3 ; x = 4 ; x = 10 ; x = 11. Leur nombre est 5. Réponse : 4. Réponse : 5.

Problèmes pour la signification physique de la dérivée

Réponse : 3 Réponse : 14

DEVOIR numéro 12 Niveau profil Mathématiques

Travail indépendant en binôme Tâche numéro 12 Niveau du profil

Aperçu:

Annexe 3 fiches individuelles n°12

1. Trouver le point maximum de la fonction1 Trouver le point minimum de la fonction

2.Trouvez le point maximum de la fonction2Trouver le point minimum de la fonction

Linnik D. Vovnenko I

1.Trouver la plus petite valeur de la fonction1. Trouvez la plus grande valeur de la fonction sur le segment

sur le segment

Vegelman V.

UNE.

1. Trouver le point maximum de la fonction1. Trouver le point minimum de la fonction

2. Trouvez la plus petite valeur de la fonction2. Trouvez la plus grande valeur de la fonction sur le segment

Sur le segment

Leontyeva A. Isaenko K.

PRATIQUE HORS AUDIT 2

Convertir des graphiques de fonction.

Cibler

Construire des graphiques de fonctions en utilisant diverses transformations, répondre à la question du problème.

Achèvement des travaux

Instructions méthodiques

Le travail est conçu pour 10 variantes, le numéro de variante coïncide avec le dernier chiffre du numéro de série dans la liste. Par exemple, 1, 11, 21, 31 ... effectuer 1 option, 2,12, 22 ... - 2 option, etc.

Le travail se compose de deux parties : la première partie de la tâche 1 - 5, ce sont des tâches qui doivent être complétées afin d'obtenir un crédit, si ces tâches sont complétées avec une erreur, elles doivent être corrigées et le travail doit être soumis à nouveau pour vérification. La deuxième partie contient des tâches, en accomplissant lesquelles vous pouvez obtenir une note supplémentaire : la partie principale +2 tâches - "4", la partie principale +3 tâches - "5".

Tâche 1. Le graphique d'une fonction linéaire est une ligne droite, deux points suffisent pour la tracer. (on prend les valeurs de l'argument x arbitrairement, et la valeur de la fonction y, on compte en la substituant dans la formule).

Pour vérifier si le graphique de la fonction passe par le point spécifié, vous devez substituer les coordonnées du point au lieu de x et y, si vous obtenez la bonne égalité, alors la ligne droite passe par le point spécifié, sinon elle ne passe pas .

Tâche 2, 3, 4. Les graphiques des fonctions spécifiées sont obtenus à partir des graphiques des fonctions , en utilisant un décalage le long de l'axe x ou y.

, nous traçons d'abord la fonction ou , puis nous le décalons d'unités "a" vers la droite ou la gauche (+ a - vers la gauche, - et vers la droite), puis nous le décalons d'unités "c" vers le haut ou vers le bas (+ b - vers le haut, -b - vers le bas)

De même avec d'autres fonctions :

Tâche 5 Pour tracer un graphique de fonction : , vous devez : 1) tracer la fonction , 2) laisser la partie du graphique qui est au-dessus de l'axe des x inchangée, 3) refléter la partie du graphique qui est au-dessous de l'axe des x.

Tâches pour une solution indépendante.

Partie obligatoire

Tâche 1. Tracer un graphique d'une fonction linéaire, déterminer si le graphique de la fonction passe par le point spécifié :

Tâche 2. Tracez un graphique d'une fonction quadratique, spécifiez l'ensemble de valeurs pour cette fonction.

Tâche 3. Construisez un graphique de la fonction, déterminez si la fonction spécifiée augmente ou diminue.

Tâche 4. Construisez un graphique de la fonction, répondez à la question du problème.

Tâche 5. Tracez le graphique de la fonction contenant le signe du module.

Tâches pour une évaluation supplémentaire.

Tâche 6. Tracez un graphique d'une fonction donnée par morceaux, déterminez s'il existe un point de rupture pour cette fonction :

Tâche 7. Déterminer combien de solutions le système d'équations a, la réponse est de justifier. Tirez des conclusions en répondant aux questions.

Quelles fonctions avez-vous tracées dans ce travail?

Comment s'appelle le graphe d'une fonction linéaire ?

Comment s'appelle le graphe d'une fonction quadratique ?

Quelles transformations de graphes connaissez-vous ?

Comment se situe le graphique d'une fonction paire dans le système de coordonnées ? Graphique de fonction impair ?

La dérivée de la fonction $ y = f (x) $ en un point donné $ x_0 $ est la limite du rapport de l'incrément de la fonction sur l'incrément correspondant de son argument, à condition que ce dernier tende vers zéro :

$ f "(x_0) = (lim) ↙ (△ x → 0) (△ f (x_0)) / (△ x) $

La différenciation est l'opération consistant à trouver une dérivée.

Table de dérivée de quelques fonctions élémentaires

Une fonction	Dérivé
$ c $	$0$
$ x $	$1$
$ x ^ n $	$ nx ^ (n-1) $
$ (1) / (x) $	$ - (1) / (x ^ 2) $
$ √x $	$ (1) / (2√x) $
$ e ^ x $	$ e ^ x $
$ lnx $	$ (1) / (x) $
$ sinx $	$ cox $
$ cox $	$ -sinx $
$ tgx $	$ (1) / (cos ^ 2x) $
$ ctgx $	$ - (1) / (péché ^ 2x) $

Règles de base pour la différenciation

1. La dérivée de la somme (différence) est égale à la somme (différence) des dérivées

$ (f (x) ± g (x)) "= f" (x) ± g "(x) $

Trouver la dérivée de la fonction $ f (x) = 3x ^ 5-cosx + (1) / (x) $

La dérivée de la somme (différence) est égale à la somme (différence) des dérivées.

$ f "(x) = (3x ^ 5)" - (cos x) "+ ((1) / (x))" = 15x ^ 4 + sinx - (1) / (x ^ 2) $

2. Dérivé de l'œuvre

$ (f (x) g (x)) "= f" (x) g (x) + f (x) g (x) "$

Trouvez la dérivée $ f (x) = 4x cosx $

$ f "(x) = (4x)" cosx + 4x (cosx) "= 4 cosx-4x sinx $

3. Dérivée du quotient

$ ((f (x)) / (g (x))) "= (f" (x) g (x) -f (x) g (x) ") / (g ^ 2 (x)) $

Trouver la dérivée $ f (x) = (5x ^ 5) / (e ^ x) $

$ f "(x) = ((5x ^ 5)" e ^ x-5x ^ 5 (e ^ x) ") / ((e ^ x) ^ 2) = (25x ^ 4 e ^ x- 5x ^ 5 e ^ x) / ((e ^ x) ^ 2) $

4. La dérivée d'une fonction complexe est égale au produit de la dérivée de la fonction externe par la dérivée de la fonction interne

$ f (g (x)) "= f" (g (x)) g "(x) $

$ f "(x) = cos" (5x) · (5x) "= - sin (5x) · 5 = -5sin (5x) $

La signification physique de la dérivée

Si un point matériel se déplace rectilignement et que sa coordonnée change en fonction du temps selon la loi $ x (t) $, alors la vitesse instantanée de ce point est égale à la dérivée de la fonction.

Le point se déplace le long de la ligne de coordonnées selon la loi $ x (t) = 1,5t ^ 2-3t + 7 $, où $ x (t) $ est la coordonnée à l'instant $ t $. A quel moment la vitesse du point sera-t-elle égale à 12$ ?

1. La vitesse est la dérivée de $ x (t) $, donc nous trouvons la dérivée de la fonction donnée

$ v (t) = x "(t) = 1,5 · 2t -3 = 3t -3 $

2. Pour trouver à quel instant $ t $ la vitesse était égale à $ 12 $, composez et résolvez l'équation :

La signification géométrique de la dérivée

Rappelons que l'équation d'une droite non parallèle aux axes de coordonnées peut être écrite sous la forme $ y = kx + b $, où $ k $ est la pente de la droite. Le coefficient $ k $ est égal à la tangente de l'angle d'inclinaison entre la droite et la direction positive de l'axe $ Ox $.

La dérivée de la fonction $ f (x) $ au point $ x_0 $ est égale à la pente $ k $ de la tangente au graphe en ce point :

On peut donc établir une égalité générale :

$ f "(x_0) = k = tgα $

Sur la figure, la tangente à la fonction $ f (x) $ augmente donc le coefficient $ k> 0 $. Puisque $ k> 0 $, alors $ f "(x_0) = tgα> 0 $. L'angle $ α $ entre la tangente et la direction positive $ Ox $ est aigu.

Dans la figure, la tangente à la fonction $ f (x) $ diminue ; par conséquent, le coefficient $ k< 0$, следовательно, $f"(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.

Sur la figure, la tangente à la fonction $ f (x) $ est parallèle à l'axe $ Ox $, donc, le coefficient $ k = 0 $, donc, $ f "(x_0) = tan α = 0 $. Le point $ x_0 $ auquel $ f "(x_0) = 0 $, appelé extrême.

La figure montre le graphe de la fonction $ y = f (x) $ et la tangente à ce graphe, tracé au point d'abscisse $ x_0 $. Trouvez la valeur de la dérivée de la fonction $ f (x) $ au point $ x_0 $.

La tangente au graphique augmente donc $ f "(x_0) = tg α> 0 $

Afin de trouver $ f"(x_0) $, trouvez la tangente de l'angle d'inclinaison entre la tangente et la direction positive de l'axe $ Ox $. Pour ce faire, ajoutez la tangente au triangle $ ABC $.

Trouvez la tangente de l'angle $ BAC $. (La tangente d'un angle aigu dans un triangle rectangle est le rapport de la jambe opposée à la jambe adjacente.)

$ tg BAC = (BC) / (AC) = (3) / (12) = (1) / (4) = 0,25 $

$ f "(x_0) = tg BAC = 0,25 $

Réponse : 0,25 $

La dérivée est également utilisée pour trouver les intervalles de fonctions croissantes et décroissantes :

Si $ f "(x)> 0 $ dans l'intervalle, alors la fonction $ f (x) $ augmente dans cet intervalle.

Si $ f "(x)< 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.

La figure montre le graphique de la fonction $ y = f (x) $. Trouvez parmi les points $ x_1, x_2, x_3… x_7 $ les points auxquels la dérivée de la fonction est négative.

En réponse, notez le nombre de points attribués.

Dans la tâche numéro 13 de l'UTILISATION en mathématiques du niveau de base, vous devrez démontrer les compétences et les connaissances d'un des concepts du comportement d'une fonction : les dérivées en un point ou les taux d'augmentation ou de diminution. La théorie sera ajoutée à cette tâche un peu plus tard, mais cela ne nous empêche pas d'analyser en détail plusieurs options typiques.

Analyse des options types pour les tâches n ° 14 de l'USE en mathématiques du niveau de base

Option 14 Mo1

Le graphique montre la dépendance de la température au temps pendant le réchauffement d'un moteur de voiture de tourisme. L'axe horizontal représente le temps en minutes écoulé depuis le démarrage du moteur ; l'axe vertical est la température du moteur en degrés Celsius.

A l'aide du graphique, attribuez à chaque intervalle de temps la caractéristique du processus de réchauffement du moteur dans cet intervalle.

Dans le tableau, sous chaque lettre, indiquez le numéro correspondant.

Algorithme d'exécution :

1. Sélectionnez l'intervalle de temps pendant lequel la température a baissé.
2. Appliquer une règle à 30°C et déterminer l'intervalle de temps pendant lequel la température était inférieure à 30°C.

Solution:

Choisissons l'intervalle de temps pendant lequel la température a baissé. Cette zone est visible à l'œil nu, elle débute 8 minutes à partir du démarrage du moteur.

Appliquez une règle à 30°C et déterminez l'intervalle de temps auquel la température était inférieure à 30°C.

Sous la règle, il y aura une section correspondant à l'intervalle de temps 0 - 1 min.

À l'aide d'un crayon et d'une règle, nous trouverons à quel intervalle de temps la température était comprise entre 40 ° C et 80 ° C.

Omettons les perpendiculaires des points correspondant à 40°C et 80°C au graphique, et des points obtenus nous omettrons les perpendiculaires à l'axe des temps.

On voit que cet intervalle de température correspond à un intervalle de temps de 3 à 6,5 minutes. C'est-à-dire parmi ceux donnés dans la condition 3 - 6 minutes.

Nous utilisons la méthode d'élimination pour sélectionner la réponse manquante.

Option 14MB2

Solution:

Analysons le graphique de la fonction A. Si la fonction augmente, alors la dérivée est positive et vice versa. La dérivée de la fonction est égale à zéro aux points extremum.

Premièrement, la fonction A augmente, c'est-à-dire la dérivée est positive. Cela correspond aux graphiques des dérivées 2 et 3. Au point maximum de la fonction x = -2, c'est-à-dire qu'en ce point la dérivée doit être nulle. Cette condition est remplie par le graphique numéro 3.

Premièrement, la fonction B diminue, c'est-à-dire la dérivée est négative. Cela correspond aux graphiques des dérivées 1 et 4. Le point maximum de la fonction est x = -2, c'est-à-dire qu'à ce point la dérivée doit être égale à zéro. Cette condition est remplie par le graphique numéro 4.

Premièrement, la fonction B augmente, c'est-à-dire la dérivée est positive. Cela correspond aux graphiques des dérivées 2 et 3. Le point maximum de la fonction x = 1, c'est-à-dire qu'en ce point la dérivée doit être égale à zéro. Cette condition est remplie par le graphique numéro 2.

Par la méthode d'élimination, nous pouvons déterminer que le graphique de la fonction correspond au graphique de la dérivée au numéro 1.

Réponse : 3421.

Option 14MB3

Algorithme d'exécution pour chacune des fonctions :

1. Déterminer les intervalles des fonctions croissantes et décroissantes.
2. Déterminer les points maximum et minimum des fonctions.
3. Tirer des conclusions, aligner les horaires proposés.

Solution:

Analysons le graphique de la fonction A.

Si la fonction est croissante, alors la dérivée est positive et vice versa. La dérivée de la fonction est égale à zéro aux points extremum.

Le point extremum est le point auquel la valeur maximale ou minimale d'une fonction est atteinte.

Premièrement, la fonction A augmente, c'est-à-dire la dérivée est positive. Cela correspond aux graphiques des dérivées 3 et 4. Au point maximum de la fonction x = 0, c'est-à-dire qu'en ce point la dérivée doit être égale à zéro. Cette condition est remplie par le graphique numéro 4.

Analysons le graphe de la fonction B.

Premièrement, la fonction B diminue, c'est-à-dire la dérivée est négative. Cela correspond aux graphiques des dérivées 1 et 2. Le point minimum de la fonction est x = -1, c'est-à-dire qu'à ce point la dérivée doit être égale à zéro. Cette condition est remplie par le graphique numéro 2.

Analysons le graphe de la fonction B.

Premièrement, la fonction B diminue, c'est-à-dire la dérivée est négative. Cela correspond aux graphiques des dérivées 1 et 2. Le point minimum de la fonction x = 0, c'est-à-dire qu'en ce point la dérivée doit être égale à zéro. Cette condition est remplie par le graphique numéro 1.

Par la méthode d'élimination, nous pouvons déterminer que le graphique de la fonction correspond au graphique de la dérivée au numéro 3.

Réponse : 4213.

Option 14MB4

La figure montre un graphique d'une fonction et des tangentes qui lui sont tracées aux points avec les abscisses A, B, C et D.La colonne de droite montre les valeurs de la dérivée aux points A, B, C et D. À l'aide du graphique, attribuez à chaque point la valeur de la dérivée de la fonction qu'il contient.

POINTS
UNE
V
AVEC
ré

LES VALEURS DU DÉRIVÉ
1) –4
2) 3
3) 2/3
4) -1/2

Rappelons ce que signifie la dérivée, à savoir sa valeur au point - la valeur de la fonction dérivée en un point est égale à la tangente de la pente (coefficient) de la tangente.

Dans les réponses, nous avons deux options positives et deux options négatives. On s'en souvient, si le coefficient d'une droite (graphique y = kx + b) positif, alors la ligne droite augmente, si elle est négative, alors la ligne droite diminue.

Nous avons deux droites ascendantes - aux points A et D. Rappelons-nous maintenant ce que signifie la valeur du coefficient k ?

Le coefficient k montre à quelle vitesse la fonction augmente ou diminue (en fait, le coefficient k lui-même est la dérivée de la fonction y = kx + b).

Par conséquent, k = 2/3 correspond à une ligne plus plate - D, et k = 3 - A.

De même, dans le cas de valeurs négatives : le point B correspond à une droite plus raide avec k = - 4, et le point C - -1/2.

Option 14MB5

Dans la figure, les points indiquent les ventes mensuelles de radiateurs dans le magasin d'électroménagers. Les mois sont affichés horizontalement et le nombre de radiateurs vendus verticalement. Pour plus de clarté, les points sont reliés par une ligne.

À l'aide de la figure, faites correspondre chacune des périodes indiquées avec une caractéristique de vente des appareils de chauffage.

Algorithme d'exécution

Nous analysons les parties du graphique correspondant aux différentes saisons. Nous formulons les situations affichées sur le graphique. Nous trouvons les options de réponse les plus appropriées pour eux.

Solution:

En hiver, le nombre de ventes dépassait les 120 pièces/mois, et il ne cessait d'augmenter. Cette situation correspond à la réponse numéro 3. Celles. on a: A - 3.

Au printemps, les ventes sont progressivement passées de 120 appareils de chauffage par mois à 50. L'option 2 est la plus proche de cette formulation. On a: B-2.

En été, le nombre de ventes n'a pas changé et a été minime. La deuxième partie de cette formulation n'est pas reflétée dans les réponses, et seul le numéro 4 convient à la première. On a donc : À 4 HEURES.

À l'automne, les ventes ont augmenté, mais leur nombre dans aucun des mois n'a dépassé 100 unités. Cette situation est décrite dans l'option #1. On a: G-1.

Option 14MB6

Le graphique montre la dépendance de la vitesse d'un bus régulier sur le temps. Sur l'axe vertical la vitesse du bus est indiquée en km/h, sur l'axe horizontal - le temps en minutes depuis le début du mouvement du bus.

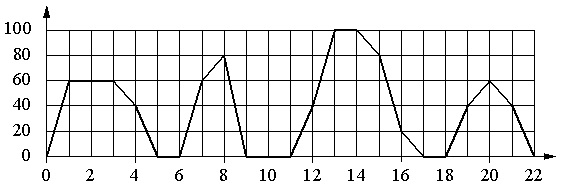
A l'aide du graphique, affectez à chaque intervalle de temps la caractéristique du mouvement du bus dans cet intervalle.

Algorithme d'exécution

1. Déterminer le prix de division sur les échelles horizontale et verticale.
2. Nous analysons tour à tour les propositions 1 à 4 de la colonne de droite ("Caractéristiques"). On les compare avec les intervalles de temps de la colonne de gauche du tableau, on trouve les couples « lettre-chiffre » pour la réponse.

Solution:

La division sur l'échelle horizontale est de 1 s, et l'échelle verticale est de 20 km/h.

1. Lorsque le bus s'arrête, sa vitesse est de 0. Le bus a eu une vitesse nulle pendant 2 minutes d'affilée uniquement de la 9e à la 11e minute. Ce temps se situe dans l'intervalle de 8 à 12 minutes. Donc, nous avons une paire pour la réponse : B-1.
2. Le bus avait une vitesse de 20 km/h et plus pendant plusieurs intervalles de temps. De plus, l'option A ne convient pas ici, car, par exemple, à la 7ème minute la vitesse était de 60 km/h, option B - car elle a déjà été appliquée, option D - car au début et à la fin de l'intervalle le bus avait une vitesse nulle... Dans ce cas, l'option B convient (12-16 min) ; à cet intervalle, le bus commence à se déplacer à une vitesse de 40 km/h, puis accélère à 100 km/m puis réduit progressivement la vitesse à 20 km/h. Nous avons donc: EN 2.
3. La limite de vitesse est définie ici. En même temps, nous ne considérons pas les options B et C. Les intervalles A et D restants conviennent tous les deux. Par conséquent, il serait correct de considérer d'abord la 4ème option, puis de revenir à la 3ème.
4. Sur les deux intervalles restants, seuls 4 à 8 minutes conviennent à la caractéristique n° 4, puisqu'il y a eu un arrêt à cet intervalle (à la 6e minute). Il n'y a eu aucun arrêt dans l'intervalle de 18 à 22 minutes. On a: A – 4... Il s'ensuit que pour la caractéristique n° 3 il faut prendre l'intervalle , c'est-à-dire il s'avère qu'un couple G-3.

Option 14MB7

La figure en pointillés montre l'augmentation de la population chinoise de 2004 à 2013. Indique horizontalement l'année, verticalement - la croissance de la population en pourcentage (augmentation de la population par rapport à l'année dernière). Pour plus de clarté, les points sont reliés par une ligne.

À l'aide de la figure, associez chacune des périodes de temps indiquées aux caractéristiques de la croissance de la population de la Chine au cours de cette période..

Algorithme d'exécution

1. Déterminer le prix de division de l'échelle verticale de l'image. Il se présente comme la différence entre une paire de valeurs d'échelle adjacentes, divisée par 2 (puisqu'il y a 2 divisions entre deux valeurs adjacentes).
2. Nous analysons séquentiellement les caractéristiques 1 à 4 données dans la condition (colonne de gauche du tableau). Nous comparons chacun d'eux avec une période de temps spécifique (colonne de droite du tableau).

Solution:

La division d'échelle verticale est de 0,01 %.

1. La baisse de la croissance s'est poursuivie de manière continue de 2004 à 2010. En 2010-2011, la croissance était stable et minime, et depuis 2012, elle a commencé à augmenter. Celles. la croissance s'est arrêtée en 2010. Cette année se situe dans la période 2009-2011. En conséquence, nous avons : EN 1.
2. La ligne descendante "la plus raide" du graphique de la figure doit être considérée comme la plus forte baisse de croissance. Il tombe sur la période 2006-2007. et est de 0,04 % par an (0,59-0,56 = 0,04 % en 2006 et 0,56-0,52 = 0,04 % en 2007). De là, nous obtenons : A - 2.
3. La croissance indiquée dans la caractéristique n°3 a commencé en 2007, s'est poursuivie en 2008 et s'est terminée en 2009. Cela correspond à la période de temps B, c'est-à-dire on a: B-3.
4. La croissance démographique a commencé à augmenter après 2011, c'est-à-dire en 2012-2013 Par conséquent, nous obtenons : G-4.

Option 14MB8

La figure montre un graphique d'une fonction et des tangentes qui lui sont tracées aux points avec les abscisses A, B, C et D.

La colonne de droite montre les valeurs de la dérivée de la fonction aux points A, B, C et D. À l'aide du graphique, attribuez à chaque point la valeur de la dérivée de la fonction qu'il contient.

Algorithme d'exécution

1. Considérons une paire de tangentes ayant un angle aigu avec la direction positive de l'axe des abscisses. Nous les comparons, trouvons une correspondance parmi la paire de valeurs correspondantes des dérivées.
2. Considérons une paire de tangentes formant un angle obtus avec la direction positive de l'axe des abscisses. Nous les comparons en valeur absolue, déterminons leur correspondance avec les valeurs des dérivées parmi les deux restant dans la colonne de droite.

Solution:

Un angle aigu avec la direction positive de l'axe des abscisses est formé par les dérivées au point B et au point C. Ces dérivés ont des valeurs positives. Par conséquent, vous devez ici choisir entre les valeurs n ° 1 et 3. En appliquant la règle selon laquelle si l'angle est inférieur à 45 0, la dérivée est inférieure à 1, et si supérieure, supérieure à 1, nous concluons: au point B, la dérivée modulo est supérieure à 1, au point C - inférieure à 1. Cela signifie que vous pouvez former des paires pour la réponse : À 3 et – 1.

Les dérivées au point A et au point D forment un angle obtus avec la direction positive de l'abscisse. Et ici on applique la même règle, en la paraphrasant un peu : plus la tangente au point est « pressée » à l'abscisse (à sa direction négative), plus elle est grande en valeur absolue. On obtient alors : la dérivée au point A est inférieure en valeur absolue à la dérivée au point D. Par conséquent, nous avons des paires pour la réponse : A - 2 et J-4.

Option 14MB9

Dans la figure, les points montrent la température quotidienne moyenne de l'air à Moscou en janvier 2011. Indique horizontalement le jour du mois, verticalement - la température en degrés Celsius. Pour plus de clarté, les points sont reliés par une ligne.

À l'aide de la figure, faites correspondre chacune des périodes de temps indiquées avec la caractéristique du changement de température.

Algorithme d'exécution

Nous analysons séquentiellement les caractéristiques 1 à 4 (colonne de droite), en utilisant le graphique de la figure. Nous mettons chacun d'eux en correspondance avec une période de temps précise (colonne de gauche).

Solution:

1. Une augmentation de la température n'a été observée qu'à la fin de la période du 22 au 28 janvier. Ici, les 27 et 28, il a augmenté respectivement de 1 et 2 degrés. À la fin de la période du 1er au 7 janvier, la température était stable (–10 degrés), à la fin des 8–14 et 15–21 janvier, elle a diminué (de –1 à –2 et de –11 à – 12 degrés, respectivement). Par conséquent, nous obtenons : G-1.
2. Étant donné que chaque période couvre 7 jours, la température doit être analysée à partir du 4e jour de chaque période. La température est restée inchangée pendant 3 à 4 jours seulement du 4 au 7 janvier. Par conséquent, nous obtenons la réponse : A - 2.
3. La température minimale mensuelle a été observée le 17 janvier. Ce nombre se situe dans la période du 15 au 21 janvier. De là, nous avons une paire: À 3.
4. Le maximum de température est tombé le 10 janvier et s'élevait à +1 degré. Cette date se situe entre le 8 et le 14 janvier. Ainsi, nous avons : B-4.

Option 14MB10

Algorithme d'exécution

1. La valeur de la fonction en un point est positive si ce point est situé au dessus de l'axe Ox.
2. La dérivée en un point est supérieure à zéro si la tangente à ce point forme un angle aigu avec la direction positive de l'axe Ox.

Solution:

Point A. Il est en dessous de l'axe Ox, ce qui signifie que la valeur de la fonction qu'il contient est négative. Si vous y dessinez une tangente, l'angle entre elle et la direction positive Ox sera d'environ 90 0, c'est-à-dire forme un angle aigu. Donc, dans ce cas, la caractéristique numéro 3 convient. Celles. on a: A - 3.

Point B. Il est situé au-dessus de l'axe Ox, c'est-à-dire point a une valeur de fonction positive. La tangente en ce point sera assez proche de l'axe des abscisses, formant un angle obtus (légèrement inférieur à 180 0) avec sa direction positive. Par conséquent, la dérivée à ce stade est négative. Ainsi convient ici la caractéristique 1. On obtient la réponse : EN 1.

Point C. Le point est situé en dessous de l'axe Ox, sa tangente forme un grand angle obtus avec la direction positive de l'axe des abscisses. Celles. au point C, la valeur à la fois de la fonction et de la dérivée est négative, ce qui correspond à la caractéristique n°2. Réponse: C-2.

Point D. Le point est au-dessus de l'axe Ox et sa tangente forme un angle aigu avec la direction positive de l'axe. Cela suggère que la valeur de la fonction et la valeur de la dérivée sont ici supérieures à zéro. Réponse: J-4.

Option 14MB11

Dans la figure, les points montrent les ventes mensuelles de réfrigérateurs dans le magasin d'électroménager. Les mois sont affichés horizontalement et le nombre de réfrigérateurs vendus verticalement. Pour plus de clarté, les points sont reliés par une ligne.

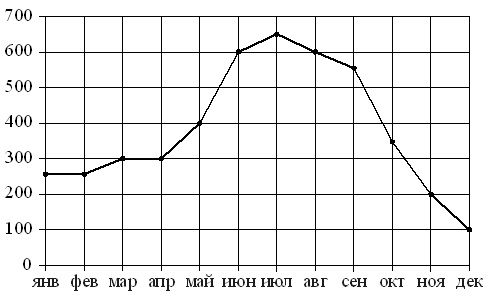
À l'aide de la figure, associez chacune des périodes indiquées à une caractéristique de vente des réfrigérateurs..