Проблем номер 1

Логиката е проста: ще действаме както преди, въпреки факта, че сега тригонометричните функции имат по-сложен аргумент!

Ако трябва да решим уравнение от вида:

Тогава ще запишем следния отговор:

Или (откакто)

Но сега имаме следния израз в нашата роля:

Тогава можете да напишете:

Нашата цел с вас е да направим лявата стойка просто, без никакви "примеси"!

Нека се отървем от тях постепенно!

Първо премахваме знаменателя при: за това умножаваме нашето равенство по:

Сега нека се отървем от него, като разделим и двете части на него:

Сега нека се отървем от осемте:

Полученият израз може да бъде записан като 2 серии от решения (по аналогия с квадратно уравнение, където или добавяме, или изваждаме дискриминанта)

Трябва да намерим най-големия отрицателен корен! Ясно е, че е необходимо да се подреди.

Помислете първо за първата серия:

Ясно е, че ако вземем, тогава в резултат ще получим положителни числа и те не представляват интерес за нас.

Така че трябва да го приемете отрицателно. Позволявам.

Когато коренът вече е:

И трябва да намерим най-големия отрицателен !! Това означава, че вече няма смисъл да се върви в негативна посока. И най-големият отрицателен корен за тази серия ще бъде.

Сега нека разгледаме втората серия:

И отново заместваме:, тогава:

Не се интересувам!

Тогава вече няма смисъл да се увеличава! Ще намалим! Нека тогава:

Приляга!

Позволявам. Тогава

Тогава - най-големият отрицателен корен!

Отговор:

Проблем номер 2

Отново решаваме, независимо от сложния косинус аргумент:

Сега отново изразяваме вляво:

Умножаваме двете страни по

Разделяме двете страни на

Всичко, което остава, е да го преместите надясно, като промените знака му от минус на плюс.

Отново имаме 2 серии корени, едната с, а другата с.

Трябва да намерим най-големия отрицателен корен. Помислете за първата серия:

Ясно е, че ще получим първия отрицателен корен при, той ще бъде равен на и ще бъде най-големият отрицателен корен в 1 серия.

За втората серия

Първият отрицателен корен също ще бъде получен при и ще бъде равен на. Тъй като тогава е най-големият отрицателен корен на уравнението.

Отговор: .

Проблем номер 3

Решете независимо от сложния аргумент за допирателна.

Изглежда, че не е нищо сложно, нали?

Както преди, ние изразяваме от лявата страна:

Е, това е страхотно, тук има само една поредица от корени! Намерете отново най-големия отрицателен.

Ясно е, че се получава, ако поставим. И този корен е равен.

Отговор:

Сега се опитайте сами да решите следните проблеми.

Домашна работа или 3 задачи за самостоятелно решение.

1. Решения-ши-те уравнение.
   
2. Решения-ши-те уравнение.
   В от-ве-тези на-пи-ши-те, най-малкият корен по-ли-тел.
3. Решения-ши-те уравнение.
   В от-ве-тези на-пи-ши-те, най-малкият корен по-ли-тел.

Готов? Проверка. Няма да описвам подробно целия алгоритъм за решение, струва ми се, че вече му е обърнато достатъчно внимание по-горе.

Е, всичко правилно ли е? О, тези гадни синуси, с тях винаги има някакви проблеми!

Е, сега можете да решите най-простите тригонометрични уравнения!

Проверете решенията и отговорите:

Проблем номер 1

Нека изразим

Най-малкият положителен корен се получава, ако поставим, тъй като, тогава

Отговор:

Проблем номер 2

Най-малкият положителен корен се получава, когато.

Ще бъде равностойно.

Отговор: .

Проблем номер 3

Когато получим, когато получим.

Отговор: .

Тези знания ще ви помогнат да решите много от проблемите, с които ще се сблъскате на изпита.

Ако кандидатствате за оценка "5", тогава просто трябва да отидете да прочетете статията за средно ниво,които ще бъдат посветени на решаването на по-сложни тригонометрични уравнения (задача C1).

СРЕДНО НИВО

В тази статия ще опиша решаване на тригонометрични уравнения от по-сложен типи как да изберем техните корени. Тук ще надграждам върху следните теми:

1. Тригонометрични уравнения за входно ниво (вижте по-горе).

По-сложните тригонометрични уравнения са в основата на по-сложни задачи. В тях се изисква както да се реши самото уравнение в общ вид, така и да се намерят корените на това уравнение, принадлежащи на определен определен интервал.

Решаването на тригонометрични уравнения се свежда до две подзадачи:

1. Решение на уравнение
2. Избор на корени

Трябва да се отбележи, че последното не винаги е задължително, но все пак се налага избор в повечето примери. И ако не се изисква, тогава можете по-скоро да симпатизирате - това означава, че уравнението е доста сложно само по себе си.

Моят опит в анализа на C1 задачи показва, че те обикновено се разделят на тези категории.

Четири категории задачи с повишена сложност (преди C1)

1. Уравнения, които се свеждат до факторизация.
2. Уравнения, свеждащи се до формата.
3. Уравнения, решени чрез промяна на променлива.
4. Уравнения, изискващи допълнителен избор на корени поради ирационалност или знаменател.

Казано по-просто: ако попаднете един от първите три вида уравнениятогава смятай себе си за късметлия. За тях, като правило, трябва допълнително да вземете корени, принадлежащи към определен интервал.

Ако попаднете на уравнение от тип 4, тогава имате по-малко късмет: трябва да се поправите малко по-дълго и по-отблизо, но доста често не изисква допълнителен избор на корени в него. Въпреки това ще анализирам този тип уравнения в следващата статия, а тази ще бъде посветена на решаването на уравнения от първите три типа.

Факторни уравнения

Най-важното нещо, което трябва да запомните, за да решавате уравнения от този тип, е

Както показва практиката, като правило това знание е достатъчно. Нека разгледаме някои примери:

Пример 1. Редуциране на уравнение до разлагане на множители с помощта на формули за редукция и синус с двоен ъгъл

• Ре-ши-те уравнение
• Не-ди-те всички корени на това уравнение

Тук, както обещах, формулите за кастинг работят:

Тогава моето уравнение ще изглежда така:

Тогава моето уравнение ще приеме следния вид:

Един късоглед ученик може да каже: а сега ще съкратя и двете части, ще получа най-простото уравнение и ще се наслаждавам на живота! И ще се обърка горчиво!

ЗАПОМНЕТЕ: НИКОГА НЕ НАМАЛЯВАЙТЕ И ДВЕТЕ ЧАСТИ НА ТРИГОНОМЕТРИЧНОТО УРАВНЕНИЕ С ФУНКЦИЯ, СЪДЪРЖАЩА НЕИЗВЕСТНО! ТАКА ГУБИТЕ КОРЕНИТЕ!

Та какво правиш? Да, всичко е просто, преместете всичко в една посока и извадете общия фактор:

Е, ние го разделяме на фактори, ура! Сега решаваме:

Първото уравнение има корени:

И второто:

Това завършва първата част от проблема. Сега трябва да изберем корените:

Пропастта е следната:

Или може да се напише и така:

Е, нека вземем корените:

Първо, нека работим с първата серия (и е по-лесно, какво да кажем!)

Тъй като нашият интервал е изцяло отрицателен, няма нужда да вземаме неотрицателни, все пак те ще дадат неотрицателни корени.

Да вземем, тогава - малко прекалено, не се вписва.

Нека, тогава - не удари отново.

Още един опит - тогава - има, удари! Намерен е първият корен!

Пак стрелям: после - пак го уцелих!

Е, още веднъж :: - това вече е полет.

Така от първата серия 2 корена принадлежат на интервала:.

Работим с втората серия (строим до степен според правилото):

Подстреляйте!

Отново подцели!

Отново подценяване!

Схванах го!

Полет!

По този начин следните корени принадлежат към моя диапазон:

По този алгоритъм ще решаваме всички останали примери. Нека практикуваме заедно с още един пример.

Пример 2. Уравнение, което се свежда до факторизация с помощта на формули за намаляване

• Решете уравнението

Решение:

Отново прословутите формули за кастинг:

Отново, не се опитвайте да намалите!

Първото уравнение има корени:

И второто:

Сега отново потърсете корените.

Ще започна с втората серия, вече знам всичко за нея от предишния пример! Вижте и се уверете, че корените, принадлежащи на празнината, са както следва:

Сега първият епизод и е по-прост:

Ако - пасва

Ако - също е добре

Ако - вече полет.

Тогава корените ще бъдат както следва:

Самостоятелна работа. 3 уравнения.

Е, техниката ясна ли ви е? Решаването на тригонометрични уравнения вече не изглежда толкова трудно? След това бързо решете сами следните проблеми, а след това вие и аз ще решим други примери:

1. Решете уравнението
   Най-ди-това са всички корени на това уравнение, прикрепени към интервала.
2. Ре-ши-те уравнение
   Посочете корените на уравнението
3. Ре-ши-те уравнение
   Най-ди-това са всички корени на това уравнение-не-ний, прикрепен-над-ле-жа-ши-про-ме-жут-ку.

Уравнение 1.

И отново формулата за леене:

Първа серия от корени:

Втора серия от корени:

Начална селекция за празнината

Отговор: , .

Уравнение 2. Проверка на самостоятелна работа.

Доста сложно групиране в фактори (ще използвам формулата за синус на двоен ъгъл):

тогава или

Това е общо решение. Сега трябва да изберем корените. Проблемът е, че не можем да кажем точната стойност на ъгъла, чийто косинус е равен на една четвърт. Следователно не мога просто да се отърва от аркосинуса - това е такъв срам!

Това, което мога да направя, е да разбера какво и как тогава.

Нека направим таблица: интервал:

Е, чрез болезнени търсения стигнахме до разочароващото заключение, че нашето уравнение има един корен на посочения интервал: \ displaystyle arccos \ frac (1) (4) -5 \ pi

Уравнение 3. Проверка на самостоятелна работа.

Плашещо уравнение. Въпреки това, той може да бъде решен доста просто чрез прилагане на формулата за синус на двойния ъгъл:

Намалете с 2:

Нека групираме първия член с втория и третия с четвъртия и изваждаме общите множители:

Ясно е, че първото уравнение няма корени, а сега разгледайте второто:

По принцип щях да се спра на решението на такива уравнения малко по-късно, но тъй като се оказа, няма какво да се направи, необходимо е да се реши ...

Уравнения от вида:

Това уравнение се решава чрез разделяне на двете части на:

По този начин нашето уравнение има една серия от корени:

Необходимо е да се намерят онези от тях, които принадлежат на интервала:.

Нека отново изградим таблица, както направих по-рано:

Отговор: .

Уравнения, които се свеждат до вида:

Е, сега е моментът да преминем към втората партида уравнения, особено след като вече избъбрих от какво се състои решението на тригонометричните уравнения от нов тип. Но няма да е излишно да повторим това уравнение от формата

Решава се чрез разделяне на двете части на косинус:

1. Ре-ши-те уравнение
   Посочете корените на уравнението-не-ниа, когато-над-лежа-от-изрязване.
2. Ре-ши-те уравнение
   Посочете корените на уравнението-не-ния, когато-над-ле-жа-ши-про-ме-жут-ку.

Пример 1.

Първата е много проста. Преместете се надясно и приложете формулата за двоен ъгъл косинус:

Аха! Уравнение на формата:. Разделям и двете части на

Правим пресяване на корените:

празнина:

Отговор:

Пример 2.

Всичко също е доста тривиално: нека разширим скобите вдясно:

Основна тригонометрична идентичност:

Синус с двоен ъгъл:

Най-накрая получаваме:

Отпадане на корена: празнина.

Отговор: .

Е, как ви харесва техниката, не е ли много сложна? Надявам се не. Веднага можем да направим резервация: в чистата си форма уравненията, които веднага се свеждат до уравнение за допирателната, са доста редки. Обикновено този преход (деление по косинус) е само част от по-сложен проблем. Ето ви пример за практикуване:

• Ре-ши-те уравнение
• Най-ди-това са всички корени на това уравнение-не-ниа, прикрепено-над-ле-джа-ши-ку.

Да проверим:

Уравнението се решава веднага, достатъчно е двете части да се разделят на:

Отпадане на корен:

Отговор: .

По един или друг начин все още не сме се срещнали с уравнения от вида, който току-що анализирахме. Все пак е твърде рано да закръгляваме: има още един „пласт“ от уравнения, който не сме анализирали. Така:

Решаване на тригонометрични уравнения чрез промяна на променлива

Тук всичко е прозрачно: разглеждаме отблизо уравнението, опростяваме го възможно най-много, правим заместване, решаваме, правим обратна замяна! На думи всичко е много лесно. Да видим в действие:

Пример.

• Решете уравнението:.
• Най-ди-това са всички корени на това уравнение-не-ниа, прикрепено-над-ле-джа-ши-ку.

Е, тук самата подмяна моли да бъде в наши ръце!

Тогава нашето уравнение ще се превърне в това:

Първото уравнение има корени:

И второто е това:

Сега ще намерим корените, принадлежащи на интервала

Отговор: .

Нека заедно да разгледаме малко по-сложен пример:

• Ре-ши-те уравнение
• Посочете корените на даденото уравнение-non-niy, when-over-le-za-shi-n-e-zhut-ku.

Тук подмяната не се вижда веднага, освен това не е много очевидна. Нека първо помислим: какво можем да направим?

Например, можем да си представим

И в същото време

Тогава моето уравнение ще приеме вида:

Сега внимание, фокус:

Нека разделим двете страни на уравнението на:

Изведнъж ти и аз получихме квадратно уравнение за! Нека направим замяна, след което получаваме:

Уравнението има следните корени:

Гадна втора серия корени, но не може да се помогне! Избираме корените в интервала.

Ние също трябва да вземем предвид това

Оттогава и тогава

Отговор:

За да се консолидирате, преди да решите проблемите сами, ето още едно упражнение за вас:

• Ре-ши-те уравнение
• Най-ди-това са всички корени на това уравнение-не-ний, прикрепен-над-ле-жа-ши-про-ме-жут-ку.

Тук трябва да държите очите си отворени: сега имаме знаменатели, които могат да бъдат нула! Ето защо трябва да бъдете особено внимателни към корените!

На първо място, трябва да трансформирам уравнението, така че да мога да направя подходящо заместване. В момента не мога да измисля нищо по-добро от това да пренапиша тангенса по отношение на синус и косинус:

Сега ще премина от косинус към синус чрез основна тригонометрична идентичност:

И накрая, ще доведа всичко до общ знаменател:

Сега мога да премина към уравнението:

Но при (тоест при).

Вече всичко е готово за подмяна:

Тогава или

Въпреки това, моля, имайте предвид, че ако, тогава в същото време!

Кой страда от това? Проблемът с допирателната, тя не е дефинирана, когато косинусът е нула (деление на нула).

Следователно корените на уравнението са както следва:

Сега отсяваме корените в интервала:

	- пасва
	- груба сила

По този начин нашето уравнение има един корен в интервала и е равно на.

Виждате: появата на знаменателя (както и допирателната, води до определени трудности с корените! Тук трябва да бъдете по-внимателни!).

Е, ние с вас почти приключихме анализа на тригонометричните уравнения, остава много малко - да решим самостоятелно две задачи. Ето ги и тях.

1. Решете уравнението
   Най-ди-това са всички корени на това уравнение-не-ниа, прикрепено-над-ле-джа-ши-ку.
2. Ре-ши-те уравнение
   Посочете корените на това уравнение, прикрепени към разреза.

Решили? Не е ли много трудно? Да проверим:

1. Работим по формулите за намаляване:

   Заместете в уравнението:

   Нека пренапишем всичко по отношение на косинуси, така че да е по-удобно да извършим замяната:

   Сега е лесно да направите замяната:

   Ясно е, че това е външен корен, тъй като уравнението няма решения. Тогава:

   Търсим нужните ни корени в интервала

   Отговор: .

2. 
   Тук подмяната се вижда веднага:

   Тогава или

   	- пасва!	- пасва!
   	- пасва!	- пасва!
   	- много!	- също много!

   Отговор:

Е, сега това е! Но решаването на тригонометричните уравнения не свършва дотук, остават ни най-трудните случаи: когато има ирационалност в уравненията или всякакви „комплексни знаменатели“. Ще разгледаме как да решим такива задачи в статията за напреднало ниво.

НАПРЕДНАЛО НИВО

В допълнение към тригонометричните уравнения, разгледани в предишните две статии, ще разгледаме друг клас уравнения, които изискват още по-внимателен анализ. Тези тригонометрични примери съдържат или ирационалност, или знаменател, което ги прави по-трудни за анализ.... Въпреки това, може да срещнете тези уравнения в част C на изпитната работа. Въпреки това, има сребърна подплата: за такива уравнения, като правило, не се повдига въпросът кой от неговите корени принадлежи към даден интервал. Нека не се бъркаме, а само тригонометрични примери.

Пример 1.

Решете уравнението и намерете корените, които принадлежат на отсечката.

Решение:

Имаме знаменател, който не трябва да е нула! Тогава решаването на това уравнение е същото като решаването на системата

Нека решим всяко едно от уравненията:

А сега второто:

Сега нека да разгледаме поредицата:

Ясно е, че опцията не ни подхожда, тъй като в този случай знаменателят е нулиран (вижте формулата за корените на второто уравнение)

Ако обаче всичко е наред, а знаменателят не е нула! Тогава корените на уравнението са както следва:,.

Сега избираме корените, принадлежащи на интервала.

	- не пасва	- пасва
	- пасва	- пасва
	груба сила	груба сила

Тогава корените са както следва:

Виждате ли, дори появата на малък шум под формата на знаменател значително повлия на решението на уравнението: изпуснахме серия от корени, които нулират знаменателя. Ситуацията може да бъде още по-трудна, ако попаднете на тригонометрични примери, които имат ирационалност.

Пример 2.

Решете уравнението:

Решение:

Е, поне няма нужда да избирате корените и това е добре! Нека първо решим уравнението, независимо от ирационалността:

Това ли е всичко? Не, уви, би било твърде лесно! Трябва да се помни, че само неотрицателни числа могат да бъдат под корена. Тогава:

Решението на това неравенство:

Сега остава да разберем дали някои от корените на първото уравнение случайно са попаднали там, където неравенството не е изпълнено.

За да направите това, можете отново да използвате таблицата:

	: , но	Не!
		Да!
		Да!

Така един от корените ми "изпадна"! Оказва се, ако го сложите. Тогава отговорът може да бъде записан по следния начин:

Отговор:

Виждате ли, коренът изисква още по-внимателно внимание! За усложняване на нещата: сега нека имам тригонометрична функция под корена.

Пример 3.

Както и преди: първо ще решим всеки поотделно, а след това ще помислим какво сме направили.

Сега второто уравнение:

Сега най-трудното нещо е да разберем дали се получават отрицателни стойности под аритметичния корен, ако заменим корените от първото уравнение там:

Числото трябва да се разбира като радиани. Тъй като радианите са около градуси, радианите са около градуси. Това е ъгълът на втората четвърт. Какъв е знакът на косинуса на втората четвърт? минус. А синусът? Плюс. И така, какво може да се каже за израза:

По-малко е от нула!

Това означава, че не е коренът на уравнението.

Сега е ред.

Нека сравним това число с нула.

Котангенсът е функция, намаляваща с 1 четвърт (колкото по-малък е аргументът, толкова по-голям е котангенсът). радианите са приблизително градуси. В същото време

от тогава и следователно
,

Отговор: .

Може ли да е още по-трудно? Вие сте добре дошъл! Ще бъде по-трудно, ако тригонометричната функция все още е под корена, а втората част на уравнението отново е тригонометричната функция.

Колкото повече тригонометрични примери, толкова по-добре, вижте по-нататък:

Пример 4.

Коренът не е подходящ поради ограничения косинус

Сега второто:

В същото време, по дефиниция на корена:

Трябва да запомним единичния кръг: а именно тези четвъртинки, където синусът е по-малък от нула. Кои квартали са? Трето и четвърто. Тогава ще се интересуваме от онези решения на първото уравнение, които се намират в третото или четвъртото тримесечие.

Първата серия произвежда корени в пресечната точка на третата и четвъртата четвърт. Втората серия, която е диаметрално противоположна на нея, поражда корени, лежащи на границата на първата и втората четвърт. Следователно тази серия не ни подхожда.

Отговор: ,

И отново тригонометрични примери с "трудна ирационалност"... Не само че отново имаме тригонометричната функция под корена, но сега тя е и в знаменателя!

Пример 5.

Е, нищо не може да се направи - действаме както преди.

Сега работим със знаменателя:

Не искам да решавам тригонометрично неравенство и затова ще действам хитро: ще взема и заменя моята поредица от корени в неравенството:

Ако - четно, тогава имаме:

тъй като тогава всички ъгли на изглед лежат в четвъртата четвърт. И отново свещеният въпрос: какъв е синусният знак в четвъртата четвърт? Отрицателно. Тогава неравенството

Ако е странно, тогава:

В коя четвърт се намира ъгълът? Това е ъгълът на втората четвърт. Тогава всички ъгли отново са ъглите на втората четвърт. Там синусът е положителен. Точно това, от което се нуждаете! Следователно поредицата:

Приляга!

Справете се с втората серия корени по същия начин:

Заместваме в нашето неравенство:

Ако - дори, тогава

Ъгли за първа четвърт. Там синусът е положителен, така че серията е подходяща. Сега, ако - нечетно, тогава:

също пасва!

Е, сега записваме отговора!

Отговор:

Е, това беше може би най-отнемащия време случай. Сега ви предлагам проблеми за ваше собствено решение.

тренировка

1. Решете и намерете всички корени на уравнението, които принадлежат на отсечката.

Решения:

1. 
   Първо уравнение:
   или
   корен на ODZ:

   Второ уравнение:

   Избиране на корени, които принадлежат на празнината

   Отговор:

Или
или
Но

Обмисли:. Ако - дори, тогава
- не пасва!
Ако - странно,: - пасва!
Това означава, че нашето уравнение има следната серия от корени:
или
Избор на корени в интервала:

	- не пасва	- пасва
	- пасва	- много
	- пасва	много

Отговор: , .

Или
Тъй като, когато допирателната не е дефинирана. Веднага изхвърляме тази поредица от корени!

Втора част:

В същото време според ОДЗ се изисква това

Проверяваме корените, намерени в първото уравнение:

Ако знакът е:

Ъгли за първа четвърт, където допирателната е положителна. Не пасва!
Ако знакът е:

Ъгъл на четвърта четвърт. Там допирателната е отрицателна. Приляга. Записваме отговора:

Отговор: , .

В тази статия сме разгледали заедно сложни тригонометрични примери, но трябва да решите сами уравненията.

ОБОБЩЕНИЕ И ОСНОВНИ ФОРМУЛИ

Тригонометричното уравнение е уравнение, в което неизвестното е строго под знака на тригонометричната функция.

Има два начина за решаване на тригонометрични уравнения:

Първият начин е използването на формули.

Вторият начин е през тригонометричния кръг.

Позволява ви да измервате ъгли, да намирате техните синуси, косинуси и др.

Подготовка за профилно ниво на единен държавен изпит по математика. Полезни материали по тригонометрия, големи теоретични видео лекции, видео анализи на задачи и селекция от задачи от минали години.

Полезни материали

Видео селекции и онлайн курсове

Тригонометрични формули

Геометрична илюстрация на тригонометрични формули

Дъгови функции. Най-прости тригонометрични уравнения

Тригонометрични уравнения

1. Необходимата теория за решаване на проблеми.
2. а) Решете уравнението $ 7 \ cos ^ 2 x - \ cos x - 8 = 0 $.
   б) Намерете всички корени на това уравнение, които принадлежат на интервала $ \ left [- \ dfrac (7 \ pi) (2); - \ dfrac (3 \ pi) (2) \ вдясно] $.
3. а) Решете уравнението $ \ dfrac (6) (\ cos ^ 2 x) - \ dfrac (7) (\ cos x) + 1 = 0 $.
   б) Намерете всички корени на това уравнение, които принадлежат на интервала $ \ left [-3 \ pi; - \ pi \ вдясно] $.
4. Решете уравнението $ \ sin \ sqrt (16 - x ^ 2) = \ dfrac12 $.
5. а) Решете уравнението $ 2 \ cos 2x - 12 \ cos x + 7 = 0 $.
   б) Намерете всички корени на това уравнение, които принадлежат на интервала $ \ left [- \ pi; \ dfrac (5 \ pi) (2) \ вдясно] $.
6. а) Решете уравнението $ \ dfrac (5) (\ mathrm (tg) ^ 2 x) - \ dfrac (19) (\ sin x) + 17 = 0 $.
   
7. Решете уравнението $ \ dfrac (2 \ cos ^ 3 x + 3 \ cos ^ 2 x + \ cos x) (\ sqrt (\ mathrm (ctg) x)) = 0 $.
8. Решете уравнението $ \ dfrac (\ mathrm (tg) ^ 3x - \ mathrm (tg) x) (\ sqrt (- \ sin x)) = 0 $.
9. 
   б) Намерете всички корени на това уравнение, които принадлежат на интервала $ \ left [- \ dfrac (5 \ pi) (2); - \ pi \ вдясно) $.
10. а) Решете уравнението $ \ cos 2x = \ sin \ left (\ dfrac (3 \ pi) (2) - x \ right) $.
    б) Намерете всички корени на това уравнение, които принадлежат на интервала $ \ left [\ dfrac (3 \ pi) (2); \ dfrac (5 \ pi) (2) \ вдясно] $.
11. а) Решете уравнението $ 2 \ sin ^ 2 \ left (\ dfrac (3 \ pi) (2) + x \ right) = \ sqrt3 \ cos x $.
    б) Намерете всички корени на това уравнение, които принадлежат на интервала $ \ left [- \ dfrac (7 \ pi) (2); -2 \ pi \ вдясно] $.

Видео анализ на задачите

б) Намерете всички корени на това уравнение, които принадлежат на отсечката $ \ left [\ sqrt (3); \ sqrt (20) \ вдясно] $.

б) Намерете всички корени на това уравнение, които принадлежат на отсечката $ \ left [- \ dfrac (9 \ pi) (2); -3 \ pi \ вдясно] $.

б) Намерете всички корени на това уравнение, които принадлежат на отсечката $ \ left [- \ sqrt (3); \ sqrt (30) \ вдясно] $.

а) Решете уравнението $ \ cos 2x = 1 - \ cos \ left (\ dfrac (\ pi) (2) - x \ right) $.
б) Намерете всички корени на това уравнение, които принадлежат на интервала $ \ left [- \ dfrac (5 \ pi) (2); - \ pi \ вдясно) $.

а) Решете уравнението $ \ cos ^ 2 (\ pi - x) - \ sin \ left (x + \ dfrac (3 \ pi) (2) \ right) = 0 $.
б) Намерете всички корени на това уравнение, които принадлежат на интервала $ \ left [\ dfrac (5 \ pi) (2); 4 \ pi \ вдясно] $.

б) Намерете всички корени на това уравнение, които принадлежат на интервала $ \ left [\ log_5 2; \ log_5 20 \ вдясно] $.

а) Решете уравнението $ 8 \ sin ^ 2 x + 2 \ sqrt (3) \ cos \ left (\ dfrac (3 \ pi) (2) - x \ right) = 9 $.
б) Намерете всички корени на това уравнение, които принадлежат на интервала $ \ left [- \ dfrac (5 \ pi) (2); - \ pi \ вдясно] $.

а) Решете уравнението $ 2 \ log_3 ^ 2 (2 \ cos x) - 5 \ log_3 (2 \ cos x) + 2 = 0 $.
б) Намерете всички корени на това уравнение, които принадлежат на интервала $ \ left [\ pi; \ dfrac (5 \ pi) (2) \ вдясно] $.

а) Решете уравнението $ \ left (\ dfrac (1) (49) \ right) ^ (\ sin x) = 7 ^ (2 \ sin 2x) $.
б) Намерете всички корени на това уравнение, които принадлежат на интервала $ \ left [\ dfrac (3 \ pi) (2); 3 \ pi \ вдясно] $.

а) Решете уравнението $ \ sin x + \ left (\ cos \ dfrac (x) (2) - \ sin \ dfrac (x) (2) \ right) \ left (\ cos \ dfrac (x) (2) + \ sin \ dfrac (x) (2) \ вдясно) = 0 $.
б) Намерете всички корени на това уравнение, които принадлежат на интервала $ \ left [\ pi; \ dfrac (5 \ pi) (2) \ вдясно] $.

а) Решете уравнението $ \ log_4 (\ sin x + \ sin 2x + 16) = 2 $.
б) Намерете всички корени на това уравнение, които принадлежат на интервала $ \ left [-4 \ pi; - \ dfrac (5 \ pi) (2) \ вдясно] $.

Селекция от задачи от минали години

1. а) Решете уравнението $ \ dfrac (\ sin x) (\ sin ^ 2 \ dfrac (x) (2)) = 4 \ cos ^ 2 \ dfrac (x) (2) $.
   б) Намерете всички корени на това уравнение, които принадлежат на отсечката $ \ left [- \ dfrac (9 \ pi) (2); -3 \ pi \ вдясно] $. (USE-2018. Ранна вълна)
2. а) Решете уравнението $ \ sqrt (x ^ 3 - 4x ^ 2 - 10x + 29) = 3 - x $.
   б) Намерете всички корени на това уравнение, които принадлежат на отсечката $ \ left [- \ sqrt (3); \ sqrt (30) \ вдясно] $. (USE-2018. Ранна вълна, резервен ден)
3. а) Решете уравнението $ 2 \ sin ^ 2 x + \ sqrt2 \ sin \ left (x + \ dfrac (\ pi) (4) \ right) = \ cos x $.
   б) Намерете всички корени на това уравнение, които принадлежат на отсечката $ \ left [-2 \ pi; - \ dfrac (\ pi) (2) \ вдясно] $. (USE-2018. Основна вълна)
4. а) Решете уравнението $ \ sqrt6 \ sin ^ 2 x + \ cos x = 2 \ sin \ left (x + \ dfrac (\ pi) (6) \ right) $.
   б) Намерете всички корени на това уравнение, които принадлежат на отсечката $ \ left [3 \ pi; \ dfrac (9 \ pi) (2) \ вдясно] $. (USE-2018. Основна вълна)
5. а) Решете уравнението $ \ sin x + 2 \ sin \ left (2x + \ dfrac (\ pi) (6) \ right) = \ sqrt3 \ sin 2x + 1 $.
   б) Намерете всички корени на това уравнение, които принадлежат на отсечката $ \ left [- \ dfrac (7 \ pi) (2); -2 \ pi \ вдясно] $. (USE-2018. Основна вълна)
6. а) Решете уравнението $ \ cos ^ 2 x + \ sin x = \ sqrt2 \ sin \ left (x + \ dfrac (\ pi) (4) \ right) $.
   б) Намерете всички корени на това уравнение, които принадлежат на отсечката $ \ left [-4 \ pi; - \ dfrac (5 \ pi) (2) \ вдясно] $. (USE-2018. Основна вълна)
7. а) Решете уравнението $ 2 \ sin \ left (2x + \ dfrac (\ pi) (3) \ right) - \ sqrt (3) \ sin x = \ sin 2x + \ sqrt3 $.
   
8. а) Решете уравнението $ 2 \ sqrt3 \ sin \ left (x + \ dfrac (\ pi) (3) \ right) - \ cos 2x = 3 \ cos x - 1 $.
   б) Намерете всички корени на това уравнение, които принадлежат на отсечката $ \ left [2 \ pi; \ dfrac (7 \ pi) (2) \ вдясно] $. (USE-2018. Основна вълна)
9. а) Решете уравнението $ 2 \ sin \ left (2x + \ dfrac (\ pi) (6) \ right) - \ cos x = \ sqrt3 \ sin 2x - 1 $.
   б) Намерете всички корени на това уравнение, които принадлежат на отсечката $ \ left [\ dfrac (5 \ pi) (2); 4 \ pi \ вдясно] $. (USE-2018. Основна вълна)
10. а) Решете уравнението $ \ sqrt2 \ sin \ left (\ dfrac (\ pi) (4) + x \ right) + \ cos 2x = \ sin x - 1 $.
    б) Намерете всички корени на това уравнение, които принадлежат на отсечката $ \ left [\ dfrac (7 \ pi) (2); 5 \ pi \ вдясно] $. (USE-2018. Основна вълна)
11. а) Решете уравнението $ \ sqrt2 \ sin \ left (2x + \ dfrac (\ pi) (4) \ right) + \ sqrt2 \ cos x = \ sin 2x - 1 $.
    б) Намерете всички корени на това уравнение, които принадлежат на отсечката $ \ left [- \ dfrac (5 \ pi) (2); - \ pi \ вдясно] $. (USE-2018. Основна вълна)
12. а) Решете уравнението $ 2 \ sin \ left (x + \ dfrac (\ pi) (3) \ right) + \ cos 2x = \ sqrt3 \ cos x + 1 $.
    б) Намерете всички корени на това уравнение, които принадлежат на отсечката $ \ left [-3 \ pi; - \ dfrac (3 \ pi) (2) \ вдясно] $. (USE-2018. Основна вълна)
13. 
    б) Намерете всички корени на това уравнение, които принадлежат на отсечката $ \ left [\ pi; \ dfrac (5 \ pi) (2) \ вдясно] $. (USE-2018. Основна вълна)
14. 
    
15. а) Решете уравнението $ 2 \ sin \ left (x + \ dfrac (\ pi) (4) \ right) + \ cos 2x = \ sqrt2 \ cos x + 1 $.
    б) Намерете всички корени на това уравнение, които принадлежат на отсечката $ \ left [\ pi; \ dfrac (5 \ pi) (2) \ вдясно] $. (USE-2018. Основна вълна, резервен ден)
16. а) Решете уравнението $ 2 \ cos x - \ sqrt3 \ sin ^ 2 x = 2 \ cos ^ 3 x $.
    б) Намерете всички корени на това уравнение, които принадлежат на отсечката $ \ left [- \ dfrac (7 \ pi) (2); -2 \ pi \ вдясно] $. (USE-2018. Основна вълна, резервен ден)
17. а) Решете уравнението $ 2 \ cos x + \ sin ^ 2 x = 2 \ cos ^ 3 x $.
    б) Намерете всички корени на това уравнение, които принадлежат на отсечката $ \ left [- \ dfrac (9 \ pi) (2); -3 \ pi \ вдясно] $. (USE-2018. Основна вълна, резервен ден)
18. а) Решете уравнението $ 2 \ sqrt2 \ sin \ left (x + \ dfrac (\ pi) (3) \ right) + 2 \ cos ^ 2 x = 2 + \ sqrt6 \ cos x $.
    б) Намерете всички корени на това уравнение, които принадлежат на отсечката $ \ left [-3 \ pi; - \ dfrac (3 \ pi) (2) \ вдясно] $. (USE-2018. Основна вълна, резервен ден)
19. а) Решете уравнението $ x - 3 \ sqrt (x - 1) + 1 = 0 $.
    б) Намерете всички корени на това уравнение, които принадлежат на отсечката $ \ left [\ sqrt (3); \ sqrt (20) \ вдясно] $. (USE-2018. Основна вълна, резервен ден)
20. а) Решете уравнението $ 2x \ cos x - 8 \ cos x + x - 4 = 0 $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [- \ dfrac (\ pi) (2); \ \ pi \ right] $. (USE-2017, основна вълна, резервен ден)
21. а) Решете уравнението $ \ log_3 (x ^ 2 - 2x) = 1 $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [\ log_2 0 (,) 2; \ \ log_2 5 \ right] $. (USE-2017, основна вълна, резервен ден)
22. а) Решете уравнението $ \ log_3 (x ^ 2 - 24x) = 4 $.
    b) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [\ log_2 0 (,) 1; \ 12 \ sqrt (5) \ right] $. (USE-2017, основна вълна, резервен ден)
23. а) Решете уравнението $ 0 (,) 4 ^ (\ sin x) + 2 (,) 5 ^ (\ sin x) = 2 $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [2 \ pi; \ \ dfrac (7 \ pi) (2) \ right] $. (USE-2017, основна вълна)
24. а) Решете уравнението $ \ log_8 \ left (7 \ sqrt (3) \ sin x - \ cos 2x - 10 \ вдясно) = 0 $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [\ dfrac (3 \ pi) (2); \ 3 \ pi \ right] $. (USE-2017, основна вълна)
25. а) Решете уравнението $ \ log_4 \ left (2 ^ (2x) - \ sqrt (3) \ cos x - 6 \ sin ^ 2 x \ right) = x $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [\ dfrac (5 \ pi) (2); \ 4 \ pi \ right] $. (USE-2017, основна вълна)
26. а) Решете уравнението $ 2 \ log_2 ^ 2 \ left (\ sin x \ right) - 5 \ log_2 \ left (\ sin x \ right) - 3 = 0 $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [- 3 \ pi; \ - \ dfrac (3 \ pi) (2) \ right] $. (USE-2017, основна вълна)
27. а) Решете уравнението $ 81 ^ (\ cos x) - 12 \ cdot 9 ^ (\ cos x) + 27 = 0 $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [- 4 \ pi; \ - \ dfrac (5 \ pi) (2) \ right] $. (USE-2017, основна вълна)
28. а) Решете уравнението $ 8 ^ x - 9 \ cdot 2 ^ (x + 1) + 2 ^ (5 - x) = 0 $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [\ log_5 2; \ \ log_5 20 \ right] $. (USE-2017, ранна вълна)
29. а) Решете уравнението $ 2 \ log ^ 2_9 x - 3 \ log_9 x + 1 = 0 $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [\ sqrt (10); \ \ sqrt (99) \ right] $. (USE-2016, основна вълна, резервен ден)
30. а) Решете уравнението $ 6 \ log ^ 2_8 x - 5 \ log_8 x + 1 = 0 $.
    b) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [2; \ 2 (,) 5 \ right] $. (USE-2016, основна вълна, резервен ден)
31. а) Решете уравнението $ \ sin 2x = 2 \ sin x + \ sin \ left (x + \ dfrac (3 \ pi) (2) \ right) + 1 $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [-4 \ pi; \ - \ dfrac (5 \ pi) (2) \ right] $. (USE-2016, основна вълна, резервен ден)
32. а) Решете уравнението $ 2 \ cos ^ 2 x + 1 = 2 \ sqrt (2) \ cos \ left (\ dfrac (3 \ pi) (2) - x \ right) $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [\ dfrac (3 \ pi) (2); \ 3 \ pi \ right] $. (USE-2016, основна вълна)
33. а) Решете уравнението $ 2 \ log ^ 2_2 (2 \ cos x) - 9 \ log_2 (2 \ cos x) + 4 = 0 $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [-2 \ pi; \ - \ dfrac (\ pi) (2) \ right] $. (USE-2016, основна вълна)
34. а) Решете уравнението $ 8 ^ x - 7 \ cdot 4 ^ x - 2 ^ (x + 4) + 112 = 0 $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [\ log_2 5; \ \ log_2 11 \ right] $. (USE-2016, ранна вълна)
35. а) Решете уравнението $ \ cos 2x + \ cos ^ 2 \ left (\ dfrac (3 \ pi) (2) - x \ right) = 0,25 $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [-4 \ pi; \ - \ dfrac (5 \ pi) (2) \ right] $. (USE-2016, ранна вълна)
36. а) Решете уравнението $ \ dfrac (13 \ sin ^ 2 x - 5 \ sin x) (13 \ cos x + 12) = 0 $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ right] $. (USE-2016, ранна вълна)
37. а) Решете уравнението $ \ dfrac (\ sin2x) (\ sin \ left (\ dfrac (7 \ pi) (2) - x \ right)) = \ sqrt (2) $.
    b) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left $. (USE-2015, основна вълна)
38. а) Решете уравнението $ 4 \ sin ^ 2 x = \ mathrm (tg) x $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [- \ pi; \ 0 \ right] $. (USE-2015, основна вълна)
39. а) Решете уравнението $ 3 \ cos 2x - 5 \ sin x + 1 = 0 $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [\ pi; \ \ dfrac (5 \ pi) (2) \ right] $. (USE-2015, основна вълна)
40. а) Решете уравнението $ \ cos 2x - 5 \ sqrt (2) \ cos x - 5 = 0 $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ right] $. (USE-2015, основна вълна)
41. а) Решете уравнението $ \ sin 2x + \ sqrt (2) \ sin x = 2 \ cos x + \ sqrt (2) $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [\ pi; \ \ dfrac (5 \ pi) (2) \ right] $. (USE-2015, ранна вълна)
42. а) Решете уравнението $ 2 \ cos ^ 3 x - \ cos ^ 2 x + 2 \ cos x - 1 = 0 $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [2 \ pi; \ \ dfrac (7 \ pi) (2) \ right] $. (USE-2015, ранна вълна)
43. а) Решете уравнението $ \ mathrm (tg) ^ 2 x + (1 + \ sqrt (3)) \ mathrm (tg) x + \ sqrt (3) = 0 $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [\ dfrac (5 \ pi) (2); \ 4 \ pi \ вдясно] $. (USE-2014, основна вълна)
44. а) Решете уравнението $ 2 \ sqrt (3) \ cos ^ 2 \ left (\ dfrac (3 \ pi) (2) + x \ right) - \ sin 2x = 0 $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [\ dfrac (3 \ pi) (2); \ 3 \ pi \ вдясно] $. (USE-2014, основна вълна)
45. а) Решете уравнението $ \ cos 2x + \ sqrt (2) \ sin \ left (\ dfrac (\ pi) (2) + x \ right) + 1 = 0 $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ вдясно] $. (USE-2014, основна вълна)
46. а) Решете уравнението $ - \ sqrt (2) \ sin \ left (- \ dfrac (5 \ pi) (2) + x \ right) \ cdot \ sin x = \ cos x $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [\ dfrac (9 \ pi) (2); \ 6 \ pi \ вдясно] $. (USE-2014, ранна вълна)
47. а) Решете уравнението $ \ sin 2x = \ sin \ left (\ dfrac (\ pi) (2) + x \ right) $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [- \ dfrac (7 \ pi) (2); \ - \ dfrac (5 \ pi) (2) \ вдясно] $. (USE-2013, основна вълна)
48. а) Решете уравнението $ 6 \ sin ^ 2 x + 5 \ sin \ left (\ dfrac (\ pi) (2) - x \ right) - 2 = 0 $.
    б) Посочете корените на това уравнение, които принадлежат на отсечката $ \ left [-5 \ pi; \ - \ dfrac (7 \ pi) (2) \ вдясно] $. (USE-2012, втора вълна)

Целта на урока:

а) за затвърждаване на умението за решаване на най-простите тригонометрични уравнения;

б) учат да избират корените на тригонометричните уравнения от даден интервал

По време на занятията.

1. Актуализация на знанията.

а) Проверка на домашната работа: на класа беше дадена изпреварваща домашна работа - да реши уравнението и да намери начин за избор на корени от даден интервал.

1) cos х= -0,5, където xI [-]. Отговор:.

2) грях х=, където xI. Отговор: ; ...

3) cos 2 х= -, където хI. Отговор:

Учениците записват решението на дъската, някой използва графика, някой използва метод за подбор.

По това време класът работи устно.

Намерете значението на израза:

а) tg - sin + cos + sin. Отговор: 1.

б) 2arccos 0 + 3 arccos 1. Отговор: ?

в) arcsin + arcsin. Отговор:.

г) 5 arctan (-) - arccos (-). Отговор:-.

- Да проверим домашните ви, да отворите тетрадките ви.

Някои от вас са намерили решение чрез метод на прилягане, а други чрез графика.

2. Заключение за решаването на тези задачи и постановката на проблема, т.е. посланието на темата и целта на урока.

- а) Трудно се решава с помощта на подбор, ако е даден голям интервал.

- б) Графичният метод не дава точни резултати, изисква проверка и отнема много време.

- Следователно трябва да има поне още един метод, най-универсалният - нека се опитаме да го намерим. И така, какво ще правим в клас днес? (Научете се да избирате корените на тригонометрично уравнение на даден интервал.)

- Пример 1 (Ученикът отива до черната дъска)

cos х= -0,5, където xI [-].

Въпрос: От какво зависи отговорът на тази задача? (От общото решение на уравнението. Нека запишем решението в общ вид). Решението е написано на таблото

х = + 2? k, където k R.

- Нека напишем това решение под формата на набор:

- Как мислите, за какъв запис на решението е удобно да изберете корени в интервала? (от втория запис). Но това отново е метод за подбор. Какво трябва да знаем, за да получим правилния отговор? (Трябва да знаете стойностите на k).

(Нека направим математически модел за намиране на k).

тъй като kI Z, то k = 0, следователно х= =	това неравенство показва, че няма цели числа на k.

заключение:За да изберете корени от даден интервал при решаване на тригонометрично уравнение, трябва:

1. за решаване на уравнение от вида sin x = a, cos x = aпо-удобно е да запишем корените на уравнението като две серии от корени.
2. за решаване на уравнения от вида tg x = a, ctg x = aзапишете общата формула за корените.
3. съставете математически модел за всяко решение под формата на двойно неравенство и намерете целочислената стойност на параметъра k или n.
4. заместете тези стойности в основната формула и ги изчислете.

3. Закотвяне.

Решете примери 2 и 3 от домашна работа, като използвате получения алгоритъм. В същото време двама ученици работят пред черната дъска, последвани от проверка на работата.

В тази статия ще се опитам да обясня 2 начина избор на корени в тригонометрично уравнение: използване на неравенства и използване на тригонометричния кръг. Нека да преминем направо към един илюстративен пример и да се заемем със случая.

A) Решете уравнението sqrt (2) cos ^ 2x = sin (Pi / 2 + x)
б) Намерете всички корени на това уравнение, принадлежащи на интервала [-7Pi / 2; -2Pi]

Нека решим точка а.

Използваме формулата за редукция за синуса sin (Pi / 2 + x) = cos (x)

Sqrt (2) cos ^ 2x = cosx

Sqrt (2) cos ^ 2x - cosx = 0

Cosx (sqrt (2) cosx - 1) = 0

X1 = Pi / 2 + Pin, n ∈ Z

Sqrt (2) cosx - 1 = 0

Cosx = 1 / sqrt (2)

Cosx = sqrt (2) / 2

X2 = arccos (sqrt (2) / 2) + 2Pin, n ∈ Z
x3 = -arccos (sqrt (2) / 2) + 2Pin, n ∈ Z

X2 = Pi / 4 + 2Pin, n ∈ Z
x3 = -Pi / 4 + 2Pin, n ∈ Z

Нека решим точка b.

1) Избор на корени с помощта на неравенства

Тук всичко се прави просто, заменяме получените корени в дадения интервал [-7Pi / 2; -2Pi], намерете целочислени стойности за n.

7Pi / 2 по-малко или равно на Pi / 2 + Pin по-малко или равно на -2Pi

Разделете всичко на Пи наведнъж

7/2 е по-малко или равно на 1/2 + n е по-малко или равно на -2

7/2 - 1/2 по-малко или равно на n по-малко или равно на -2 - 1/2

4 по-малко или равно на n по-малко или равно на -5/2

Цялото число n в този диапазон е -4 и -3. Така че корените, принадлежащи на този интервал, ще бъдат Pi / 2 + Pi (-4) = -7Pi / 2, Pi / 2 + Pi (-3) = -5Pi / 2

По същия начин правим още две неравенства

7Pi / 2 по-малко или равно на Pi / 4 + 2Pin по-малко или равно на -2Pi
-15/8 по-малко или равно на n по-малко или равно на -9/8

В този интервал няма цяло число n

7Pi / 2 по-малко или равно на -Pi / 4 + 2Pin по-малко или равно на -2Pi
-13/8 по-малко или равно на n по-малко или равно на -7/8

Едно цяло число n в този интервал е -1. Така избраният корен на този интервал е -Pi / 4 + 2Pi * (- 1) = -9Pi / 4.

Така че отговорът в точка b: -7Pi / 2, -5Pi / 2, -9Pi / 4

2) Избиране на корени с помощта на тригонометричен кръг

За да използвате този метод, трябва да разберете как работи този кръг. Ще се опитам да обясня на прост език как разбирам това. Мисля, че в училищата в уроците по алгебра тази тема беше обяснявана многократно с умните думи на учителя, сложните формулировки в учебниците. Лично аз разбирам това като окръжност, която може да се премине безкраен брой пъти, поради факта, че функциите синус и косинус са периодични.

Да отидем веднъж обратно на часовниковата стрелка

Нека обиколим 2 пъти обратно на часовниковата стрелка

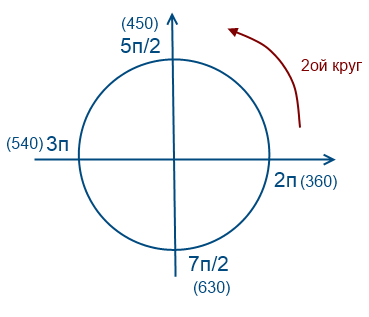
Нека заобиколим 1 път по часовниковата стрелка (стойностите ще бъдат отрицателни)

Нека се върнем на нашия въпрос, трябва да изберем корени в интервала [-7Pi / 2; -2Pi]

За да стигнете до числата -7Pi / 2 и -2Pi, трябва да обиколите кръга обратно на часовниковата стрелка два пъти. За да се намерят корените на уравнението на този интервал, е необходимо да се оцени и замени.

Помислете за x = Pi / 2 + Pin. Каква е приблизителната стойност на n за стойността на x да бъде някъде в този интервал? Замествайки, да речем -2, получаваме Pi / 2 - 2Pi = -3Pi / 2, очевидно това не е включено в нашия интервал, така че вземаме по-малко от -3, Pi / 2 - 3Pi = -5Pi / 2, пасва, нека опитаме -4 отново, Pi / 2 - 4Pi = -7Pi / 2 също е подходящ.

Разсъждавайки по подобен начин за Pi / 4 + 2Pin и -Pi / 4 + 2Pin, намираме друг корен -9Pi / 4.

Сравнение на двата метода.

Първият метод (използвайки неравенства) е много по-надежден и много по-лесен за разбиране, но ако наистина се занимавате сериозно с тригонометричния кръг и втория метод за подбор, тогава изборът на корени ще бъде много по-бърз, можете да спестите около 15 минути на Изпитът.

а) Решете уравнението:.

б) Намерете всички корени на това уравнение, които принадлежат на отсечката.

Решението на проблема

Този урок разглежда пример за решаване на тригонометрично уравнение, което може да се използва като пример за решаване на задачи от тип C1 при подготовка за изпита по математика.

На първо място се определя обхватът на функцията - всички разрешени стойности на аргумента. След това, по време на решението, тригонометричната синусова функция се преобразува в косинус с помощта на формулата за намаляване. Освен това всички членове на уравнението се прехвърлят в лявата му страна, където общият фактор се изважда от скобите. Всеки фактор е равен на нула, което ви позволява да определите корените на уравнението. Тогава корените, принадлежащи към дадения сегмент, се определят по метода на завоите. За да направите това, върху построения единичен кръг се маркира цикъл от лявата граница на посочения сегмент вдясно. Освен това, намерените корени на единичната окръжност се свързват чрез сегменти с неговия център и се определят точките, в които тези сегменти пресичат контура. Тези пресечни точки са желаният отговор на втората част на задачата.