Problem številka 1
Logika je preprosta: ravnali bomo tako kot prej, kljub dejstvu, da imajo trigonometrične funkcije zdaj bolj zapleten argument!
Če bi rešili enačbo v obliki:
Nato bi zapisali naslednji odgovor:
ali (odkar)
Toda zdaj imamo v svoji vlogi naslednji izraz:
Potem lahko napišeš:
Naš cilj z vami je narediti levo stojalo preprosto, brez »nečistoč«!
Znebimo se jih postopoma!
Najprej odstranimo imenovalec pri: za to pomnožimo našo enakost z:
Zdaj se ga znebimo tako, da nanj razdelimo oba dela:
Zdaj pa se znebimo osmih:
Nastali izraz lahko zapišemo kot 2 niza rešitev (po analogiji s kvadratno enačbo, kjer bodisi dodamo ali odštejemo diskriminanta)
Najti moramo največji negativni koren! Jasno je, da je treba urediti.
Najprej razmislite o prvi seriji:
Jasno je, da če vzamemo, bomo posledično dobili pozitivne številke in nas ne zanimajo.
Zato ga morate vzeti negativno. Pustiti.
Ko je koren že:
In najti moramo največjega negativnega!! Pomeni, da ni več smiselno iti v negativno smer. In največji negativni koren za to serijo bo.
Zdaj pa poglejmo drugo serijo:
In spet nadomestimo:, nato:
Ne zanima!
Potem nima smisla več povečevati! Zmanjšali bomo! Naj potem:
ustreza!
Pustiti. Potem
Potem - največji negativni koren!
odgovor:
Problem številka 2
Ponovno rešimo, ne glede na kompleksni kosinusni argument:
Zdaj ponovno izrazimo levo:
Obe strani pomnožimo z
Obe strani razdelimo na
Vse, kar ostane, je, da ga premaknete v desno in spremenite njegov predznak iz minusa v plus.
Spet imamo 2 seriji korenin, eno z in drugo z.
Najti moramo največji negativni koren. Razmislite o prvi seriji:
Jasno je, da bomo prejeli prvi negativni koren pri, ta bo enak in bo največji negativni koren v 1 seriji.
Za drugo serijo
Prvi negativni koren bo prav tako pridobljen pri in bo enak. Ker je potem največji negativni koren enačbe.
odgovor: .
Problem številka 3
Rešite ne glede na kompleksni tangentni argument.
Zdi se, da to ni nič zapletenega, kajne?
Kot prej na levi strani izrazimo:
No, to je super, tukaj je samo ena serija korenin! Ponovno poiščite največjo negativno.
Jasno je, da se izkaže, če damo. In ta koren je enak.
odgovor:
Zdaj poskusite sami rešiti naslednje težave.
Domača naloga ali 3 naloge za samostojno rešitev.
- Odločitve-shi-te enačba.
- Odločitve-shi-te enačba.
V ot-ve-tistih na-pi-shi-te, najmanjši po-li-tel-root. - Odločitve-shi-te enačba.
V ot-ve-tistih na-pi-shi-te, najmanjši po-li-tel-root.
pripravljeni? Preverjanje. Ne bom podrobno opisoval celotnega algoritma rešitve, zdi se mi, da mu je bilo zgoraj že posvečeno dovolj pozornosti.
No, je vse pravilno? Oh, ti grdi sinusi, z njimi je vedno nekaj težav!
No, zdaj lahko rešite najpreprostejše trigonometrične enačbe!
Preverite rešitve in odgovore:
Problem številka 1
Naj izrazimo
Najmanjši pozitivni koren dobimo, če damo, saj, potem
odgovor:
Problem številka 2
Najmanjši pozitivni koren dobimo, ko.
Enako bo.
odgovor: .
Problem številka 3
Ko dobimo, ko dobimo.
odgovor: .
To znanje vam bo pomagalo rešiti številne težave, s katerimi se boste soočili na izpitu.
Če se prijavljate za oceno "5", potem morate le prebrati članek srednji nivo, ki bo namenjen reševanju zahtevnejših trigonometričnih enačb (naloga C1).
POVPREČNA RAVEN
V tem članku bom opisal reševanje trigonometričnih enačb bolj zapletenega tipa in kako izbrati njihove korenine. Tukaj bom gradil na naslednjih temah:
- Trigonometrične enačbe za začetni nivo (glej zgoraj).
Kompleksnejše trigonometrične enačbe so osnova bolj zapletenih problemov. V njih je potrebno tako rešiti samo enačbo v splošni obliki kot poiskati korenine te enačbe, ki pripadajo določenemu določenemu intervalu.
Reševanje trigonometričnih enačb se zmanjša na dve podnalogi:
- Rešitev enačbe
- Izbira korenin
Opozoriti je treba, da slednje ni vedno potrebno, vendar je v večini primerov vseeno potrebna izbira. In če ni potrebno, potem lahko raje sočustvujete - to pomeni, da je enačba sama po sebi precej zapletena.
Moje izkušnje pri razčlenjevanju nalog C1 kažejo, da so običajno razdeljene v te kategorije.
Štiri kategorije nalog večje kompleksnosti (prej C1)
- Enačbe, ki se reducirajo na faktorizacijo.
- Enačbe reducirajo na obliko.
- Enačbe, rešene s spremembo spremenljivke.
- Enačbe, ki zahtevajo dodatno izbiro korenin zaradi iracionalnosti ali imenovalca.
Preprosto povedano: če naletite ena od prvih treh vrst enačb potem se imej za srečo. Zanje morate praviloma dodatno pobrati korenine, ki pripadajo določenemu intervalu.
Če naletite na enačbo tipa 4, potem imate manj sreče: z njo se morate ukvarjati malo dlje in natančneje, vendar pogosto ne zahteva dodatne izbire korenin v njej. Kljub temu bom to vrsto enačb analiziral v naslednjem članku, ta pa bo namenjen reševanju enačb prvih treh vrst.
Faktorske enačbe
Najpomembnejša stvar, ki si jo je treba zapomniti pri reševanju enačb te vrste, je
Kot kaže praksa, je to znanje praviloma dovolj. Poglejmo si nekaj primerov:
Primer 1. Redukcija enačbe na faktorizacijo z uporabo redukcijskih formul in dvojnega kotnega sinusa
- Res-shi-te enačba
- Ne-di-te vse korenine te enačbe
Tukaj, kot sem obljubil, formule za ulivanje delujejo:
Potem bo moja enačba videti takole:
Potem bo moja enačba dobila naslednjo obliko:
Kratkovidni študent bi lahko rekel: zdaj pa bom oba dela skrajšal, dobil najpreprostejšo enačbo in užival življenje! In hudo se bo zmotilo!
| ZAPOMNITE: NIKOLI NE ZMANJŠUJTE OBEH DELOV TRIGONOMETRIČNE ENAČBE S FUNKCIJO, KI VSEBUJE NEZNANO! TAKO IZGUBITE KORENINE! |
Torej kaj počneš? Da, vse je preprosto, premaknite vse v eno smer in odstranite skupni faktor:
No, upoštevamo faktorje, hura! Zdaj se odločimo:
Prva enačba ima korenine:
In drugi:
S tem je prvi del problema končan. Zdaj moramo izbrati korenine:
Vrzel je taka:
Lahko pa se zapiše tudi takole:
No, vzemimo korenine:
Najprej delajmo s prvo serijo (in to je lažje, kaj naj rečemo!)
Ker je naš interval popolnoma negativen, ni treba jemati nenegativnih, vseeno bodo dali nenegativne korenine.
Vzemimo, potem - malo preveč, ne ustreza.
Naj, potem - ni spet zadel.
Še en poskus - potem - tu je, zadeti! Najden prvi koren!
Spet streljam: potem - spet sem zadel!
No, še enkrat:: - to je že let.
Torej iz prve serije 2 korena pripadata intervalu:.
Delamo z drugo serijo (gradimo do stopnje po pravilu):
Premalo!
Spet premalo!
Spet premalo!
Razumem!
Let!
Tako mojemu razponu pripadajo naslednje korenine:
Po tem algoritmu bomo rešili vse ostale primere. Vadimo skupaj s še enim primerom.
Primer 2. Enačba, ki se reducira na faktorizacijo z uporabo redukcijskih formul
- Reši enačbo
rešitev:
Spet zloglasne formule za ulivanje:
Še enkrat, ne poskušajte zmanjšati!
Prva enačba ima korenine:
In drugi:
Zdaj znova poiščite korenine.
Začel bom z drugo serijo, vse o njej vem že iz prejšnjega primera! Poglejte in se prepričajte, da so korenine, ki pripadajo vrzeli, naslednje:
Zdaj prva epizoda in je preprostejša:
Če - ustreza
Če - je tudi dobro
Če - že let.
Potem bodo korenine naslednje:
Samostojno delo. 3 enačbe.
No, ti je tehnika jasna? Reševanje trigonometričnih enačb se ne zdi več tako težko? Nato sami hitro rešite naslednje težave, potem pa bomo z vami rešili še druge primere:
- Reši enačbo
Ne-di-to so vse korenine te enačbe, pritrjene na interval. - Res-shi-te enačba
Navedite korenine enačbe - Res-shi-te enačba
Ne-di-to so vse korenine te enačbe-non-niy, pripeto-over-le-zha-shi-pro-me-zhut-ku.
enačba 1.
In spet formula za ulivanje:
Prva serija korenin:
Druga serija korenin:
Začetek izbire za vrzel
Odgovor: , .
2. enačba. Preverjanje samostojnega dela.
Precej zapleteno združevanje v faktorje (uporabil bom formulo dvojnega kotnega sinusa):
potem oz
To je splošna rešitev. Zdaj moramo izbrati korenine. Težava je v tem, da ne moremo povedati natančne vrednosti kota, katerega kosinus je enak eni četrtini. Zato se ne morem kar tako znebiti arkosinusa - to je taka škoda!
Kar lahko storim, je ugotoviti, kaj in kako, potem.
Naredimo tabelo: interval:
No, z bolečim iskanjem smo prišli do razočaranja, da ima naša enačba en koren v navedenem intervalu: \ displaystyle arccos \ frac (1) (4) -5 \ pi
Enačba 3. Preverjanje samostojnega dela.
Zastrašujoča enačba. Vendar pa je to mogoče enostavno rešiti z uporabo formule dvojnega kotnega sinusa:
Zmanjšaj za 2:
Prvi člen združimo z drugim in tretjega s četrtim ter izločimo skupne faktorje:
Jasno je, da prva enačba nima korenin, zdaj pa razmislite o drugi:
Na splošno sem se želel malo kasneje osredotočiti na rešitev takšnih enačb, a ker se je izkazalo, potem ni kaj storiti, treba je rešiti ...
Enačbe v obliki:
Ta enačba se reši tako, da oba dela delimo z:
Tako ima naša enačba eno samo serijo korenin:
Treba je najti tiste od njih, ki pripadajo intervalu:.
Znova sestavimo tabelo, kot sem naredil prej:
Odgovor: .
Enačbe, ki se reducirajo na obliko:
No, zdaj je čas, da preidemo na drugo serijo enačb, še posebej, ker sem že brbljal, iz česa je sestavljena rešitev trigonometričnih enačb novega tipa. Vendar ne bo odveč ponoviti te enačbe v obliki
Reši se tako, da oba dela delimo s kosinusom:
- Res-shi-te enačba
Označi korenine enačbe-ne-nia, ko-pre-leži-od-rezanja. - Res-shi-te enačba
Navedite korenine enačbe-not-nia, when-over-le-zha-shi-pro-me-zhut-ku.
Primer 1.
Prva je zelo preprosta. Premaknite se v desno in uporabite formulo dvojnega kota kosinusa:
Aha! Enačba v obliki:. Oba dela razdelim na
Presejemo korenine:
vrzel:
odgovor:
Primer 2.
Vse je tudi precej trivialno: razširimo oklepaje na desni:
Osnovna trigonometrična identiteta:
Dvojni kotni sinus:
Končno dobimo:
Izpad korenin: vrzel.
Odgovor: .
No, kako vam je všeč tehnika, ni preveč zapletena? Upam, da ne. Takoj lahko naredimo pridržek: v svoji čisti obliki so enačbe, ki se takoj zmanjšajo na enačbo za tangento, precej redke. Običajno je ta prehod (delitev s kosinusom) le del bolj zapletenega problema. Tukaj je primer za vadbo:
- Res-shi-te enačba
- Ne-di-to so vse korenine te enačbe-ne-nia, pritrjena-nad-le-zha-shi-ku.
Preverimo:
Enačba je takoj rešena, dovolj je, da oba dela razdelimo na:
Izpad korenine:
Odgovor: .
Tako ali drugače se še nismo srečali z enačbami, ki smo jih pravkar analizirali. Vendar je za zaokroževanje še prezgodaj: obstaja še ena "plast" enačb, ki je nismo analizirali. Torej:
Reševanje trigonometričnih enačb s spreminjanjem spremenljivke
Tu je vse pregledno: natančno pogledamo enačbo, jo čim bolj poenostavimo, naredimo zamenjavo, rešimo, naredimo obratno zamenjavo! Z besedami je vse zelo enostavno. Poglejmo v akciji:
Primer.
- Reši enačbo:.
- Ne-di-to so vse korenine te enačbe-ne-nia, pritrjena-nad-le-zha-shi-ku.
No, tu pa že sama zamenjava prosi, da je v naših rokah!
Potem se bo naša enačba spremenila v tole:
Prva enačba ima korenine:
In drugi je ta:
Zdaj bomo našli korenine, ki pripadajo intervalu
Odgovor: .
Pojdimo skupaj na nekoliko bolj zapleten primer:
- Res-shi-te enačba
- Navedite korenine dane enačbe-non-niy, when-over-le-za-shi-n-e-zhut-ku.
Tukaj zamenjava ni takoj vidna, poleg tega ni zelo očitna. Najprej pomislimo: kaj lahko storimo?
Na primer, lahko si predstavljamo
In hkrati
Potem bo moja enačba dobila obliko:
Zdaj pozornost, fokus:
Delimo obe strani enačbe z:
Nenadoma sva ti in jaz dobila kvadratno enačbo za! Naredimo zamenjavo, potem dobimo:
Enačba ima naslednje korenine:
Neprijetna druga serija korenin, vendar se ne da! V intervalu izberemo korenine.
To moramo tudi upoštevati
Od in takrat
odgovor:
Za utrjevanje, preden sami rešite težave, je tu še ena vaja za vas:
- Res-shi-te enačba
- Ne-di-to so vse korenine te enačbe-non-niy, pripeto-over-le-zha-shi-pro-me-zhut-ku.
Tukaj morate imeti odprte oči: zdaj imamo imenovalce, ki so lahko nič! Zato morate biti še posebej pozorni na korenine!
Najprej moram enačbo preoblikovati, da lahko naredim primerno zamenjavo. Trenutno si ne morem zamisliti nič boljšega kot prepisati tangento v smislu sinusa in kosinusa:
Zdaj bom šel od kosinusa do sinusa po osnovni trigonometrični identiteti:
In končno, bom vse skupaj spravil v skupni imenovalec:
Zdaj lahko grem na enačbo:
Toda pri (torej pri).
Zdaj je vse pripravljeno za zamenjavo:
Potem pa tudi
Vendar upoštevajte, da če, potem hkrati!
Kdo trpi zaradi tega? Težava s tangento, je nedefinirana, ko je kosinus nič (deljenje z nič).
Tako so korenine enačbe naslednje:
Zdaj presejemo korenine v intervalu:
| - ustreza | |
| - surova sila |
Tako ima naša enačba en sam koren v intervalu in je enaka.
Vidite: videz imenovalca (kot tudi tangente, vodi do določenih težav s koreninami! Tukaj morate biti bolj previdni!).
No, z vami sva skoraj končala analizo trigonometričnih enačb, ostalo je zelo malo - samostojno rešiti dva problema. Tukaj so.
- Reši enačbo
Ne-di-to so vse korenine te enačbe-ne-nia, pritrjena-nad-le-zha-shi-ku. - Res-shi-te enačba
Navedite korenine te enačbe, pritrjene na rez.
Odločil? Ni zelo težko? Preverimo:
- Delamo po redukcijskih formulah:
Zamenjaj v enačbo:
Prepišimo vse v smislu kosinusov, tako da je bolj priročno opraviti zamenjavo:
Zdaj je enostavno narediti zamenjavo:
Jasno je, da gre za tuj koren, saj enačba nima rešitev. Nato:
V intervalu iščemo korenine, ki jih potrebujemo
Odgovor: .
Tukaj je zamenjava takoj vidna:Potem pa tudi
- ustreza! - ustreza! - ustreza! - ustreza! - veliko! - tudi veliko! odgovor:
No, zdaj je to to! Toda reševanje trigonometričnih enačb se s tem ne konča, preostanejo nam najtežji primeri: ko je v enačbah iracionalnost ali različne vrste "kompleksnih imenovalcev". Kako rešiti takšne naloge, bomo razmislili v članku za napredno raven.
NAPREDNI NIVO
Poleg trigonometričnih enačb, obravnavanih v prejšnjih dveh člankih, bomo obravnavali še en razred enačb, ki zahtevajo še bolj natančno analizo. Ti trigonometrični primeri vsebujejo bodisi iracionalnost bodisi imenovalec, zaradi česar jih je težje analizirati.... Vendar pa boste morda naleteli na te enačbe v delu C izpitnega dela. Vendar pa obstaja srebrna podloga: za takšne enačbe se praviloma ne postavlja vprašanje, katera od njegovih korenin pripada določenemu intervalu. Da ne tepemo po grmu, ampak le trigonometrične primere.
Primer 1.
Rešite enačbo in poiščite korenine, ki pripadajo segmentu.
rešitev:
Imamo imenovalec, ki ne sme biti nič! Potem je reševanje te enačbe enako reševanju sistema
Rešimo vsako od enačb:
In zdaj drugo:
Zdaj pa si poglejmo serijo:
Jasno je, da nam možnost ne ustreza, saj je v tem primeru imenovalec ničel (glej formulo za korene druge enačbe)
Če pa je potem vse v redu in imenovalec ni nič! Potem so korenine enačbe naslednje:,.
Zdaj izberemo korenine, ki pripadajo intervalu.
| - ne ustreza | - ustreza | |
| - ustreza | - ustreza | |
| surova sila | surova sila |
Potem so korenine naslednje:
Vidite, tudi pojav majhnega šuma v obliki imenovalca je bistveno vplival na rešitev enačbe: spustili smo vrsto korenin, ki imenujejo nič. Situacija je lahko še težja, če naletite na trigonometrične primere, ki imajo iracionalnost.
Primer 2.
Reši enačbo:
rešitev:
No, vsaj korenin ni treba izbrati in to je dobro! Najprej rešimo enačbo, ne glede na iracionalnost:
Je to vse? Ne, žal, bilo bi prelahko! Ne smemo pozabiti, da so pod korenom lahko samo nenegativna števila. Nato:
Rešitev te neenakosti:
Zdaj je treba še ugotoviti, ali je katera od korenin prve enačbe po naključju prišla tja, kjer neenakost ni izpolnjena.
Če želite to narediti, lahko znova uporabite tabelo:
| : , ampak | Ne! | |
| Ja! | ||
| Ja! |
Tako mi je "izpadla" ena od korenin! Izkazalo se je, če ga postavite. Potem lahko odgovor zapišemo takole:
odgovor:
Vidite, koren zahteva še večjo pozornost! Da zakompliciram: zdaj naj imam trigonometrično funkcijo pod korenom.
Primer 3.
Kot doslej: najprej bomo rešili vsakega posebej, nato pa razmislili, kaj smo naredili.
Zdaj druga enačba:
Zdaj je najtežje ugotoviti, ali dobimo negativne vrednosti pod aritmetičnim korenom, če tam nadomestimo korene iz prve enačbe:
Število je treba razumeti kot radiane. Ker so radiani približno stopinje, so radiani približno stopinje. To je kotiček druge četrtine. Kakšen je znak kosinusa druge četrtine? Minus. In sinus? plus. Torej, kaj lahko rečemo o izrazu:
Je manj kot nič!
To pomeni, da ni koren enačbe.
Zdaj je na vrsti.
Primerjajmo to številko z ničlo.
Kotangens je funkcija, ki se zmanjša za 1 četrtino (manjši kot je argument, večji je kotangens). radiani so približno stopinje. Ob istem času
od takrat in od tod
,
Odgovor: .
Bi lahko bilo še težje? Ni za kaj! Težje bo, če je trigonometrična funkcija še vedno pod korenom, drugi del enačbe pa je spet trigonometrična funkcija.
Več trigonometričnih primerov, bolje, glej dalje:
Primer 4.
Koren ni primeren zaradi omejenega kosinusa
Zdaj pa drugo:
Hkrati po definiciji korena:
Zapomniti si moramo enotni krog: in sicer tiste četrtine, kjer je sinus manjši od nič. Katere četrti so? Tretji in četrti. Potem nas bodo zanimale tiste rešitve prve enačbe, ki ležijo v tretji ali četrti četrtini.
Prva serija daje korenine na presečišču tretje in četrte četrtine. Druga serija, ki je diametralno nasprotna njej, daje korenine, ki ležijo na meji prve in druge četrtine. Zato nam ta serija ne ustreza.
Odgovor: ,
In spet trigonometrični primeri s "težko iracionalnostjo"... Ne samo, da imamo trigonometrično funkcijo spet pod korenom, ampak je zdaj tudi v imenovalcu!
Primer 5.
No, nič se ne da narediti - ravnamo kot prej.
Zdaj delamo z imenovalcem:
Ne želim reševati trigonometrične neenakosti, zato bom ravnal zvit: vzel bom in nadomestil svojo serijo korenin v neenakost:
Če - celo, potem imamo:
saj so potem vsi zorni koti v četrti četrtini. In spet sveto vprašanje: kakšen je sinusni znak v četrti četrtini? Negativno. Nato neenakost
Če je čudno, potem:
V kateri četrtini leži vogal? To je kotiček druge četrtine. Nato so vsi vogali spet vogali druge četrtine. Sinus je tam pozitiven. Samo tisto, kar potrebujete! Torej serija:
ustreza!
Na enak način ravnajte z drugo serijo korenin:
V svoji neenakosti nadomestimo:
Če - celo, potem
Koti prve četrtine. Sinus je tam pozitiven, zato je serija primerna. Zdaj, če je - čudno, potem:
tudi ustreza!
No, zdaj pa zapišemo odgovor!
odgovor:
No, to je bil morda najbolj zamuden primer. Zdaj vam ponujam probleme za lastno rešitev.
Telovaditi
- Rešite in poiščite vse korene enačbe, ki pripadajo segmentu.
rešitve:
Prva enačba:
oz
koren ODZ:Druga enačba:
Izbira korenin, ki pripadajo vrzeli
odgovor:
ali
oz
Ampak
Upoštevajte:. Če - celo, potem
- ne ustreza!
Če - liho,: - ustreza!
To pomeni, da ima naša enačba naslednjo serijo korenin:
oz
Izbira korenin v intervalu:
| - ne ustreza | - ustreza | |
| - ustreza | - veliko | |
| - ustreza | veliko |
Odgovor: , .
ali
Ker, ko tangenta ni definirana. To serijo korenin takoj zavržemo!
drugi del:
Hkrati se po mnenju ODZ zahteva, da
Preverimo korenine, ki jih najdemo v prvi enačbi:
Če je znak:
Koti prve četrtine, kjer je tangenta pozitivna. Ne ustreza!
Če je znak:
Kot četrte četrtine. Tam je tangenta negativna. Prilega se. Odgovor zapišemo:
Odgovor: , .
V tem članku smo skupaj obravnavali zapletene trigonometrične primere, vendar bi morali enačbe rešiti sami.
POVZETEK IN OSNOVNE FORMULE
Trigonometrična enačba je enačba, v kateri je neznanka strogo pod znakom trigonometrične funkcije.
Obstajata dva načina za reševanje trigonometričnih enačb:
Prvi način je uporaba formul.
Druga pot je skozi trigonometrični krog.
Omogoča merjenje kotov, iskanje njihovih sinusov, kosinusov in še več.
Priprava na profilno stopnjo enotnega državnega izpita iz matematike. Uporabno gradivo o trigonometriji, velika teoretična video predavanja, video analize problemov in izbor nalog iz preteklih let.
Uporabni materiali
Video izbori in spletni tečaji
Trigonometrične formule
Geometrijska ilustracija trigonometričnih formul
Obločne funkcije. Najenostavnejše trigonometrične enačbe
Trigonometrične enačbe
- Potrebna teorija za reševanje problemov.
- a) Reši enačbo $ 7 \ cos ^ 2 x - \ cos x - 8 = 0 $.
b) Poišči vse korene te enačbe, ki pripadajo intervalu $ \ left [- \ dfrac (7 \ pi) (2); - \ dfrac (3 \ pi) (2) \ desno] $. - a) Rešite enačbo $ \ dfrac (6) (\ cos ^ 2 x) - \ dfrac (7) (\ cos x) + 1 = 0 $.
b) Poišči vse korene te enačbe, ki pripadajo intervalu $ \ left [-3 \ pi; - \ pi \ desno] $. - Rešite enačbo $ \ sin \ sqrt (16 - x ^ 2) = \ dfrac12 $.
- a) Rešite enačbo $ 2 \ cos 2x - 12 \ cos x + 7 = 0 $.
b) Poišči vse korene te enačbe, ki pripadajo intervalu $ \ left [- \ pi; \ dfrac (5 \ pi) (2) \ desno] $. - a) Reši enačbo $ \ dfrac (5) (\ mathrm (tg) ^ 2 x) - \ dfrac (19) (\ sin x) + 17 = 0 $.
- Rešite enačbo $ \ dfrac (2 \ cos ^ 3 x + 3 \ cos ^ 2 x + \ cos x) (\ sqrt (\ mathrm (ctg) x)) = 0 $.
- Rešite enačbo $ \ dfrac (\ mathrm (tg) ^ 3x - \ mathrm (tg) x) (\ sqrt (- \ sin x)) = 0 $.
b) Poišči vse korene te enačbe, ki pripadajo intervalu $ \ left [- \ dfrac (5 \ pi) (2); - \ pi \ desno) $.- a) Reši enačbo $ \ cos 2x = \ sin \ levo (\ dfrac (3 \ pi) (2) - x \ desno) $.
b) Poišči vse korene te enačbe, ki pripadajo intervalu $ \ left [\ dfrac (3 \ pi) (2); \ dfrac (5 \ pi) (2) \ desno] $. - a) Reši enačbo $ 2 \ sin ^ 2 \ levo (\ dfrac (3 \ pi) (2) + x \ desno) = \ sqrt3 \ cos x $.
b) Poišči vse korene te enačbe, ki pripadajo intervalu $ \ left [- \ dfrac (7 \ pi) (2); -2 \ pi \ desno] $.
Video analiza nalog
b) Poišči vse korene te enačbe, ki pripadajo odseku $ \ left [\ sqrt (3); \ sqrt (20) \ desno] $.
b) Poišči vse korene te enačbe, ki pripadajo odseku $ \ left [- \ dfrac (9 \ pi) (2); -3 \ pi \ desno] $.
b) Poišči vse korene te enačbe, ki pripadajo odseku $ \ left [- \ sqrt (3); \ sqrt (30) \ desno] $.
a) Reši enačbo $ \ cos 2x = 1 - \ cos \ levo (\ dfrac (\ pi) (2) - x \ desno) $.
b) Poišči vse korene te enačbe, ki pripadajo intervalu $ \ left [- \ dfrac (5 \ pi) (2); - \ pi \ desno) $.
a) Rešite enačbo $ \ cos ^ 2 (\ pi - x) - \ sin \ levo (x + \ dfrac (3 \ pi) (2) \ desno) = 0 $.
b) Poišči vse korene te enačbe, ki pripadajo intervalu $ \ left [\ dfrac (5 \ pi) (2); 4 \ pi \ desno] $.
b) Poiščite vse korene te enačbe, ki pripadajo intervalu $ \ left [\ log_5 2; \ log_5 20 \ desno] $.
a) Reši enačbo $ 8 \ sin ^ 2 x + 2 \ sqrt (3) \ cos \ levo (\ dfrac (3 \ pi) (2) - x \ desno) = 9 $.
b) Poišči vse korene te enačbe, ki pripadajo intervalu $ \ left [- \ dfrac (5 \ pi) (2); - \ pi \ desno] $.
a) Rešite enačbo $ 2 \ log_3 ^ 2 (2 \ cos x) - 5 \ log_3 (2 \ cos x) + 2 = 0 $.
b) Poišči vse korene te enačbe, ki pripadajo intervalu $ \ left [\ pi; \ dfrac (5 \ pi) (2) \ desno] $.
a) Reši enačbo $ \ levo (\ dfrac (1) (49) \ desno) ^ (\ sin x) = 7 ^ (2 \ sin 2x) $.
b) Poišči vse korene te enačbe, ki pripadajo intervalu $ \ left [\ dfrac (3 \ pi) (2); 3 \ pi \ desno] $.
a) Reši enačbo $ \ sin x + \ levo (\ cos \ dfrac (x) (2) - \ sin \ dfrac (x) (2) \ desno) \ levo (\ cos \ dfrac (x) (2)) + \ sin \ dfrac (x) (2) \ desno) = 0 $.
b) Poišči vse korene te enačbe, ki pripadajo intervalu $ \ left [\ pi; \ dfrac (5 \ pi) (2) \ desno] $.
a) Rešite enačbo $ \ log_4 (\ sin x + \ sin 2x + 16) = 2 $.
b) Poišči vse korene te enačbe, ki pripadajo intervalu $ \ left [-4 \ pi; - \ dfrac (5 \ pi) (2) \ desno] $.
Izbor nalog iz preteklih let
- a) Rešite enačbo $ \ dfrac (\ sin x) (\ sin ^ 2 \ dfrac (x) (2)) = 4 \ cos ^ 2 \ dfrac (x) (2) $.
b) Poišči vse korene te enačbe, ki pripadajo odseku $ \ left [- \ dfrac (9 \ pi) (2); -3 \ pi \ desno] $. (USE-2018. Zgodnji val) - a) Reši enačbo $ \ sqrt (x ^ 3 - 4x ^ 2 - 10x + 29) = 3 - x $.
b) Poišči vse korene te enačbe, ki pripadajo odseku $ \ left [- \ sqrt (3); \ sqrt (30) \ desno] $. (USE-2018. Zgodnji val, rezervni dan) - a) Reši enačbo $ 2 \ sin ^ 2 x + \ sqrt2 \ sin \ levo (x + \ dfrac (\ pi) (4) \ desno) = \ cos x $.
b) Poišči vse korene te enačbe, ki pripadajo odseku $ \ left [-2 \ pi; - \ dfrac (\ pi) (2) \ desno] $. (USE-2018. Glavni val) - a) Rešite enačbo $ \ sqrt6 \ sin ^ 2 x + \ cos x = 2 \ sin \ levo (x + \ dfrac (\ pi) (6) \ desno) $.
b) Poišči vse korene te enačbe, ki pripadajo odseku $ \ left [3 \ pi; \ dfrac (9 \ pi) (2) \ desno] $. (USE-2018. Glavni val) - a) Reši enačbo $ \ sin x + 2 \ sin \ levo (2x + \ dfrac (\ pi) (6) \ desno) = \ sqrt3 \ sin 2x + 1 $.
b) Poišči vse korene te enačbe, ki pripadajo odseku $ \ left [- \ dfrac (7 \ pi) (2); -2 \ pi \ desno] $. (USE-2018. Glavni val) - a) Reši enačbo $ \ cos ^ 2 x + \ sin x = \ sqrt2 \ sin \ levo (x + \ dfrac (\ pi) (4) \ desno) $.
b) Poišči vse korene te enačbe, ki pripadajo odseku $ \ left [-4 \ pi; - \ dfrac (5 \ pi) (2) \ desno] $. (USE-2018. Glavni val) - a) Reši enačbo $ 2 \ sin \ levo (2x + \ dfrac (\ pi) (3) \ desno) - \ sqrt (3) \ sin x = \ sin 2x + \ sqrt3 $.
- a) Reši enačbo $ 2 \ sqrt3 \ sin \ levo (x + \ dfrac (\ pi) (3) \ desno) - \ cos 2x = 3 \ cos x - 1 $.
b) Poišči vse korene te enačbe, ki pripadajo odseku $ \ left [2 \ pi; \ dfrac (7 \ pi) (2) \ desno] $. (USE-2018. Glavni val) - a) Reši enačbo $ 2 \ sin \ levo (2x + \ dfrac (\ pi) (6) \ desno) - \ cos x = \ sqrt3 \ sin 2x - 1 $.
b) Poišči vse korene te enačbe, ki pripadajo odseku $ \ left [\ dfrac (5 \ pi) (2); 4 \ pi \ desno] $. (USE-2018. Glavni val) - a) Reši enačbo $ \ sqrt2 \ sin \ levo (\ dfrac (\ pi) (4) + x \ desno) + \ cos 2x = \ sin x - 1 $.
b) Poišči vse korene te enačbe, ki pripadajo odseku $ \ left [\ dfrac (7 \ pi) (2); 5 \ pi \ desno] $. (USE-2018. Glavni val) - a) Reši enačbo $ \ sqrt2 \ sin \ levo (2x + \ dfrac (\ pi) (4) \ desno) + \ sqrt2 \ cos x = \ sin 2x - 1 $.
b) Poišči vse korene te enačbe, ki pripadajo odseku $ \ left [- \ dfrac (5 \ pi) (2); - \ pi \ desno] $. (USE-2018. Glavni val) - a) Reši enačbo $ 2 \ sin \ levo (x + \ dfrac (\ pi) (3) \ desno) + \ cos 2x = \ sqrt3 \ cos x + 1 $.
b) Poišči vse korene te enačbe, ki pripadajo odseku $ \ left [-3 \ pi; - \ dfrac (3 \ pi) (2) \ desno] $. (USE-2018. Glavni val)
b) Poišči vse korene te enačbe, ki pripadajo odseku $ \ left [\ pi; \ dfrac (5 \ pi) (2) \ desno] $. (USE-2018. Glavni val)- a) Rešite enačbo $ 2 \ sin \ levo (x + \ dfrac (\ pi) (4) \ desno) + \ cos 2x = \ sqrt2 \ cos x + 1 $.
b) Poišči vse korene te enačbe, ki pripadajo odseku $ \ left [\ pi; \ dfrac (5 \ pi) (2) \ desno] $. (USE-2018. Glavni val, rezervni dan) - a) Reši enačbo $ 2 \ cos x - \ sqrt3 \ sin ^ 2 x = 2 \ cos ^ 3 x $.
b) Poišči vse korene te enačbe, ki pripadajo odseku $ \ left [- \ dfrac (7 \ pi) (2); -2 \ pi \ desno] $. (USE-2018. Glavni val, rezervni dan) - a) Reši enačbo $ 2 \ cos x + \ sin ^ 2 x = 2 \ cos ^ 3 x $.
b) Poišči vse korene te enačbe, ki pripadajo odseku $ \ left [- \ dfrac (9 \ pi) (2); -3 \ pi \ desno] $. (USE-2018. Glavni val, rezervni dan) - a) Reši enačbo $ 2 \ sqrt2 \ sin \ levo (x + \ dfrac (\ pi) (3) \ desno) + 2 \ cos ^ 2 x = 2 + \ sqrt6 \ cos x $.
b) Poišči vse korene te enačbe, ki pripadajo odseku $ \ left [-3 \ pi; - \ dfrac (3 \ pi) (2) \ desno] $. (USE-2018. Glavni val, rezervni dan) - a) Rešite enačbo $ x - 3 \ sqrt (x - 1) + 1 = 0 $.
b) Poišči vse korene te enačbe, ki pripadajo odseku $ \ left [\ sqrt (3); \ sqrt (20) \ desno] $. (USE-2018. Glavni val, rezervni dan) - a) Rešite enačbo $ 2x \ cos x - 8 \ cos x + x - 4 = 0 $.
b) Navedite korenine te enačbe, ki pripadajo odseku $ \ levo [- \ dfrac (\ pi) (2); \ \ pi \ desno] $. (USE-2017, glavni val, rezervni dan) - a) Rešite enačbo $ \ log_3 (x ^ 2 - 2x) = 1 $.
b) Označi korenine te enačbe, ki pripadajo odseku $ \ levo [\ log_2 0 (,) 2; \ \ log_2 5 \ desno] $. (USE-2017, glavni val, rezervni dan) - a) Rešite enačbo $ \ log_3 (x ^ 2 - 24x) = 4 $.
b) Označi korenine te enačbe, ki pripadajo odseku $ \ levo [\ log_2 0 (,) 1; \ 12 \ sqrt (5) \ desno] $. (USE-2017, glavni val, rezervni dan) - a) Reši enačbo $ 0 (,) 4 ^ (\ sin x) + 2 (,) 5 ^ (\ sin x) = 2 $.
b) Označi korenine te enačbe, ki pripadajo odseku $ \ levo [2 \ pi; \ \ dfrac (7 \ pi) (2) \ desno] $. (USE-2017, glavni val) - a) Reši enačbo $ \ log_8 \ levo (7 \ sqrt (3) \ sin x - \ cos 2x - 10 \ desno) = 0 $.
b) Navedite korenine te enačbe, ki pripadajo odseku $ \ left [\ dfrac (3 \ pi) (2); \ 3 \ pi \ right] $. (USE-2017, glavni val) - a) Rešite enačbo $ \ log_4 \ levo (2 ^ (2x) - \ sqrt (3) \ cos x - 6 \ sin ^ 2 x \ desno) = x $.
b) Navedite korenine te enačbe, ki pripadajo odseku $ \ left [\ dfrac (5 \ pi) (2); \ 4 \ pi \ right] $. (USE-2017, glavni val) - a) Reši enačbo $ 2 \ log_2 ^ 2 \ levo (\ sin x \ desno) - 5 \ log_2 \ levo (\ sin x \ desno) - 3 = 0 $.
b) Označi korenine te enačbe, ki pripadajo odseku $ \ levo [- 3 \ pi; \ - \ dfrac (3 \ pi) (2) \ desno] $. (USE-2017, glavni val) - a) Reši enačbo $ 81 ^ (\ cos x) - 12 \ cdot 9 ^ (\ cos x) + 27 = 0 $.
b) Označi korenine te enačbe, ki pripadajo odseku $ \ levo [- 4 \ pi; \ - \ dfrac (5 \ pi) (2) \ desno] $. (USE-2017, glavni val) - a) Reši enačbo $ 8 ^ x - 9 \ cdot 2 ^ (x + 1) + 2 ^ (5 - x) = 0 $.
b) Označi korenine te enačbe, ki pripadajo odseku $ \ levo [\ log_5 2; \ \ log_5 20 \ desno] $. (USE-2017, zgodnji val) - a) Reši enačbo $ 2 \ log ^ 2_9 x - 3 \ log_9 x + 1 = 0 $.
b) Navedite korenine te enačbe, ki pripadajo odseku $ \ left [\ sqrt (10); \ \ sqrt (99) \ right] $. (USE-2016, glavni val, rezervni dan) - a) Reši enačbo $ 6 \ log ^ 2_8 x - 5 \ log_8 x + 1 = 0 $.
b) Označi korenine te enačbe, ki pripadajo odseku $ \ levo [2; \ 2 (,) 5 \ desno] $. (USE-2016, glavni val, rezervni dan) - a) Reši enačbo $ \ sin 2x = 2 \ sin x + \ sin \ levo (x + \ dfrac (3 \ pi) (2) \ desno) + 1 $.
b) Navedite korenine te enačbe, ki pripadajo odseku $ \ left [-4 \ pi; \ - \ dfrac (5 \ pi) (2) \ right] $. (USE-2016, glavni val, rezervni dan) - a) Rešite enačbo $ 2 \ cos ^ 2 x + 1 = 2 \ sqrt (2) \ cos \ levo (\ dfrac (3 \ pi) (2) - x \ desno) $.
b) Navedite korenine te enačbe, ki pripadajo odseku $ \ left [\ dfrac (3 \ pi) (2); \ 3 \ pi \ right] $. (USE-2016, glavni val) - a) Reši enačbo $ 2 \ log ^ 2_2 (2 \ cos x) - 9 \ log_2 (2 \ cos x) + 4 = 0 $.
b) Navedite korenine te enačbe, ki pripadajo odseku $ \ left [-2 \ pi; \ - \ dfrac (\ pi) (2) \ right] $. (USE-2016, glavni val) - a) Reši enačbo $ 8 ^ x - 7 \ cdot 4 ^ x - 2 ^ (x + 4) + 112 = 0 $.
b) Označi korenine te enačbe, ki pripadajo odseku $ \ levo [\ log_2 5; \ \ log_2 11 \ desno] $. (USE-2016, zgodnji val) - a) Rešite enačbo $ \ cos 2x + \ cos ^ 2 \ levo (\ dfrac (3 \ pi) (2) - x \ desno) = 0,25 $.
b) Navedite korenine te enačbe, ki pripadajo odseku $ \ left [-4 \ pi; \ - \ dfrac (5 \ pi) (2) \ right] $. (USE-2016, zgodnji val) - a) Rešite enačbo $ \ dfrac (13 \ sin ^ 2 x - 5 \ sin x) (13 \ cos x + 12) = 0 $.
b) Navedite korenine te enačbe, ki pripadajo odseku $ \ left [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ right] $. (USE-2016, zgodnji val) - a) Rešite enačbo $ \ dfrac (\ sin2x) (\ sin \ left (\ dfrac (7 \ pi) (2) - x \ desno)) = \ sqrt (2) $.
b) Navedite korenine te enačbe, ki pripadajo odseku $ \ left $. (USE-2015, glavni val) - a) Reši enačbo $ 4 \ sin ^ 2 x = \ mathrm (tg) x $.
b) Navedite korenine te enačbe, ki pripadajo odseku $ \ levo [- \ pi; \ 0 \ desno] $. (USE-2015, glavni val) - a) Reši enačbo $ 3 \ cos 2x - 5 \ sin x + 1 = 0 $.
b) Navedite korenine te enačbe, ki pripadajo odseku $ \ left [\ pi; \ \ dfrac (5 \ pi) (2) \ right] $. (USE-2015, glavni val) - a) Rešite enačbo $ \ cos 2x - 5 \ sqrt (2) \ cos x - 5 = 0 $.
b) Navedite korenine te enačbe, ki pripadajo odseku $ \ left [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ right] $. (USE-2015, glavni val) - a) Reši enačbo $ \ sin 2x + \ sqrt (2) \ sin x = 2 \ cos x + \ sqrt (2) $.
b) Navedite korenine te enačbe, ki pripadajo odseku $ \ left [\ pi; \ \ dfrac (5 \ pi) (2) \ right] $. (USE-2015, zgodnji val) - a) Reši enačbo $ 2 \ cos ^ 3 x - \ cos ^ 2 x + 2 \ cos x - 1 = 0 $.
b) Označi korenine te enačbe, ki pripadajo odseku $ \ levo [2 \ pi; \ \ dfrac (7 \ pi) (2) \ desno] $. (USE-2015, zgodnji val) - a) Reši enačbo $ \ mathrm (tg) ^ 2 x + (1 + \ sqrt (3)) \ mathrm (tg) x + \ sqrt (3) = 0 $.
b) Navedite korenine te enačbe, ki pripadajo odseku $ \ left [\ dfrac (5 \ pi) (2); \ 4 \ pi \ desno] $. (USE-2014, glavni val) - a) Reši enačbo $ 2 \ sqrt (3) \ cos ^ 2 \ levo (\ dfrac (3 \ pi) (2) + x \ desno) - \ sin 2x = 0 $.
b) Navedite korenine te enačbe, ki pripadajo odseku $ \ left [\ dfrac (3 \ pi) (2); \ 3 \ pi \ desno] $. (USE-2014, glavni val) - a) Reši enačbo $ \ cos 2x + \ sqrt (2) \ sin \ left (\ dfrac (\ pi) (2) + x \ desno) + 1 = 0 $.
b) Navedite korenine te enačbe, ki pripadajo odseku $ \ left [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ desno] $. (USE-2014, glavni val) - a) Rešite enačbo $ - \ sqrt (2) \ sin \ left (- \ dfrac (5 \ pi) (2) + x \ desno) \ cdot \ sin x = \ cos x $.
b) Navedite korenine te enačbe, ki pripadajo odseku $ \ left [\ dfrac (9 \ pi) (2); \ 6 \ pi \ desno] $. (USE-2014, zgodnji val) - a) Reši enačbo $ \ sin 2x = \ sin \ levo (\ dfrac (\ pi) (2) + x \ desno) $.
b) Navedite korenine te enačbe, ki pripadajo odseku $ \ left [- \ dfrac (7 \ pi) (2); \ - \ dfrac (5 \ pi) (2) \ desno] $. (USE-2013, glavni val) - a) Reši enačbo $ 6 \ sin ^ 2 x + 5 \ sin \ levo (\ dfrac (\ pi) (2) - x \ desno) - 2 = 0 $.
b) Navedite korenine te enačbe, ki pripadajo odseku $ \ left [-5 \ pi; \ - \ dfrac (7 \ pi) (2) \ desno] $. (USE-2012, drugi val)
Namen lekcije:
a) utrditi sposobnost reševanja najpreprostejših trigonometričnih enačb;
b) naučiti izbrati korenine trigonometričnih enačb iz danega intervala
Med poukom.
1. Aktualizacija znanja.
a) Preverjanje domače naloge: razred je dobil vnaprejšnjo domačo nalogo - rešiti enačbo in poiskati način za izbiro korenin iz danega intervala.
1) cos x= -0,5, kjer je xI [-]. odgovor:.
2) greh x=, kjer je xI. Odgovor: ; ...
3) cos 2 x= -, kjer je хI. odgovor:
Učenci zapišejo rešitev na tablo, nekdo z grafom, nekdo z izbirno metodo.
V tem času razred deluje ustno.
Poiščite pomen izraza:
a) tg - sin + cos + sin. Odgovor: 1.
b) 2arccos 0 + 3 arccos 1. Odgovor: ?
c) arcsin + arcsin. odgovor:.
d) 5 arctan (-) - arccos (-). Odgovor: -.
- Preverimo domačo nalogo, odprimo zvezke z domačimi nalogami.
Nekateri ste našli rešitev z metodo fit, drugi pa z grafom.
2. Sklep o tem, kako rešiti te naloge in postavitev problema, torej sporočilo teme in namen lekcije.
- a) Težko je rešiti s pomočjo selekcije, če je podan velik interval.
- b) Grafična metoda ne daje točnih rezultatov, zahteva preverjanje in vzame veliko časa.
- Zato mora obstajati vsaj še ena metoda, najbolj univerzalna - poskusimo jo najti. Kaj bomo torej počeli danes v razredu? (Naučite se izbrati korenine trigonometrične enačbe v danem intervalu.)
- Primer 1 (Študent gre do table)
cos x= -0,5, kjer je xI [-].
Vprašanje: Od česa je odvisen odgovor na to nalogo? (Iz splošne rešitve enačbe. Zapišimo rešitev v splošni obliki). Odločitev je zapisana na tabli
х = + 2? k, kjer je k R.
- Zapišimo to rešitev v obliki niza:

- Kaj menite, za kateri zapis rešitve je priročno izbrati korenine v intervalu? (iz drugega vnosa). Ampak to je spet izbirna metoda. Kaj moramo vedeti, da dobimo pravi odgovor? (Poznati morate vrednosti k).
(Naredimo matematični model, da najdemo k).
ker je kI Z, potem je k = 0, torej X= = |
ta neenakost kaže, da ni celih vrednosti k. |
zaključek:Če želite izbrati korenine iz danega intervala pri reševanju trigonometrične enačbe, morate:
- rešiti enačbo v obliki sin x = a, cos x = a bolj priročno je korenine enačbe zapisati kot dve vrsti korenin.
- rešiti enačbe v obliki tg x = a, ctg x = a zapišite splošno formulo za korenine.
- sestavi matematični model za vsako rešitev v obliki dvojne neenakosti in poišče celo število parametra k ali n.
- nadomestite te vrednosti v korensko formulo in jih izračunajte.
Rešite primera 2 in 3 iz domače naloge po pridobljenem algoritmu. Hkrati za tablo delata dva učenca, čemur sledi preverjanje dela.
V tem članku bom poskušal razložiti 2 načina izbor korenin v trigonometrični enačbi: z uporabo neenakosti in uporabo trigonometričnega kroga. Pojdimo naravnost na ilustrativni primer in obravnavajmo primer.
A) Reši enačbo sqrt (2) cos ^ 2x = sin (Pi / 2 + x)
b) Poiščite vse korene te enačbe, ki pripadajo intervalu [-7Pi / 2; -2Pi]
Rešimo točko a.
Uporabimo redukcijsko formulo za sinusni sin (Pi / 2 + x) = cos (x)
Sqrt (2) cos ^ 2x = cosx
Sqrt (2) cos ^ 2x - cosx = 0
Cosx (sqrt (2) cosx - 1) = 0
X1 = Pi / 2 + Pin, n ∈ Z
Sqrt (2) cosx - 1 = 0
Cosx = 1 / sqrt (2)
Cosx = sqrt (2) / 2
X2 = arccos (sqrt (2) / 2) + 2Pin, n ∈ Z
x3 = -arccos (sqrt (2) / 2) + 2Pin, n ∈ Z
X2 = Pi / 4 + 2Pin, n ∈ Z
x3 = -Pi / 4 + 2Pin, n ∈ Z
Rešimo točko b.
1) Izbira korenin z uporabo neenakosti
Tukaj je vse narejeno preprosto, dobljene korene nadomestimo v danem intervalu [-7Pi / 2; -2Pi], poiščite cele vrednosti za n.
7Pi / 2 manj kot ali enako Pi / 2 + Pin manjši ali enak -2Pi
Vse razdelite na Pi naenkrat
7/2 je manjše ali enako 1/2 + n je manjše ali enako -2
7/2 - 1/2 manjše ali enako n manjše ali enako -2 - 1/2
4 manjša ali enaka n manjša ali enaka -5/2
Celo število n v tem območju je -4 in -3. Torej bodo korenine, ki pripadajo temu intervalu, Pi / 2 + Pi (-4) = -7Pi / 2, Pi / 2 + Pi (-3) = -5Pi / 2
Podobno naredimo še dve neenakosti
7Pi / 2 manjše ali enako Pi / 4 + 2Pin manjše ali enako -2Pi
-15/8 manjše ali enako n manjše ali enako -9/8
V tem intervalu ni celega števila n
7Pi / 2 manj kot ali enako -Pi / 4 + 2Pin manj kot ali enako -2Pi
-13/8 manjše ali enako n manjše ali enako -7/8
Eno celo število n v tem razponu je -1. Torej je izbrani koren na tem intervalu -Pi / 4 + 2Pi * (- 1) = -9Pi / 4.
Torej odgovor v točki b: -7Pi / 2, -5Pi / 2, -9Pi / 4
2) Izbira korenin s trigonometričnim krogom
Če želite uporabiti to metodo, morate razumeti, kako deluje ta krog. Poskušal bom v preprostem jeziku razložiti, kako to razumem. Mislim, da so v šolah pri pouku algebre to temo večkrat razlagali s pametnimi besedami učitelja, zapletenimi formulacijami v učbenikih. Osebno to razumem kot krog, ki ga je mogoče prehoditi neskončno število krat, zaradi dejstva, da sta sinusni in kosinusni funkciji periodični.
Gremo enkrat v nasprotni smeri urinega kazalca
Obrnimo se 2-krat v nasprotni smeri urinega kazalca
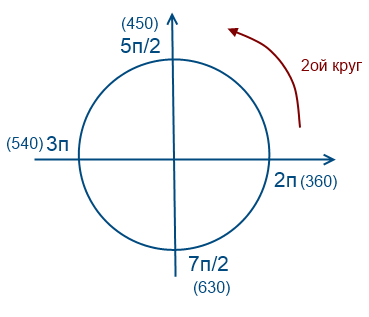
Obrnimo se 1-krat v smeri urinega kazalca (vrednosti bodo negativne)

Vrnimo se k našemu vprašanju, korenine moramo izbrati v intervalu [-7Pi / 2; -2Pi]
Če želite priti do številk -7Pi / 2 in -2Pi, morate dvakrat zaobiti krog v nasprotni smeri urinega kazalca. Da bi našli korenine enačbe na tem intervalu, je treba oceniti in nadomestiti.
Upoštevajte x = Pi / 2 + Pin. Kakšna je približna vrednost n, da je vrednost x nekje v tem intervalu? Če zamenjamo, recimo -2, dobimo Pi / 2 - 2Pi = -3Pi / 2, očitno to ni vključeno v naš interval, zato vzamemo manj kot -3, Pi / 2 - 3Pi = -5Pi / 2, ustreza, poskusimo znova -4, primeren je tudi Pi / 2 - 4Pi = -7Pi / 2.
Podobno razmišljamo za Pi / 4 + 2Pin in -Pi / 4 + 2Pin, najdemo še en koren -9Pi / 4.

Primerjava obeh metod.
Prva metoda (z uporabo neenakosti) je veliko bolj zanesljiva in veliko lažje razumljiva, če pa se res resno ukvarjate s trigonometričnim krogom in drugo izbirno metodo, bo izbira korenin veliko hitrejša, prihranite lahko približno 15 minut. izpit.
a) Reši enačbo:.
b) Poišči vse korene te enačbe, ki pripadajo segmentu.
Rešitev problema

Ta lekcija obravnava primer reševanja trigonometrične enačbe, ki jo lahko uporabimo kot primer za reševanje nalog tipa C1 pri pripravi na izpit iz matematike.
Najprej se določi obseg funkcije - vse dovoljene vrednosti argumenta. Nato se med reševanjem trigonometrična sinusna funkcija pretvori v kosinus z uporabo redukcijske formule. Nadalje se vsi členi enačbe prenesejo na njeno levo stran, kjer je skupni faktor vzet iz oklepajev. Vsak faktor je nastavljen na nič, kar vam omogoča, da določite korenine enačbe. Nato se korenine, ki pripadajo danemu segmentu, določijo z metodo zavojev. Da bi to naredili, je na konstruiranem krogu enote označena zanka od leve meje določenega segmenta proti desni. Nadalje so najdene korenine na enotnem krogu povezane s segmenti z njegovim središčem in določene so točke, na katerih ti segmenti sekajo zanko. Te presečišča so želeni odgovor na drugi del problema.

































