Premica y = 3x + 2 je tangentna na graf funkcije y = -12x ^ 2 + bx-10. Poiščite b, glede na to, da je abscisa dotične točke manjša od nič.

Pokaži rešitev

Rešitev

Naj bo x_0 abscisa točke na grafu funkcije y = -12x ^ 2 + bx-10, skozi katero poteka tangenta na ta graf.

Vrednost odvoda v točki x_0 je enaka naklonu tangente, to je y "(x_0) = - 24x_0 + b = 3. Po drugi strani pa tangentna točka pripada obema grafoma funkcije in tangenta, to je -12x_0 ^ 2 + bx_0-10 = 3x_0 + 2. Dobimo sistem enačb \ začetek (primeri) -24x_0 + b = 3, \\ - 12x_0 ^ 2 + bx_0-10 = 3x_0 + 2. \ konec (primeri)

Če rešimo ta sistem, dobimo x_0 ^ 2 = 1, kar pomeni bodisi x_0 = -1 ali x_0 = 1. Glede na pogoj je abscisa dotične točke manjša od nič, torej x_0 = -1, potem je b = 3 + 24x_0 = -21.

Odgovori

Stanje

Slika prikazuje graf funkcije y = f (x) (ki je lomljena črta, sestavljena iz treh ravnih odsekov). S pomočjo slike izračunajte F (9) -F (5), kjer je F (x) eden od antiderivov f (x).

Pokaži rešitev

Rešitev

Po formuli Newton-Leibniz je razlika F (9) -F (5), kjer je F (x) eden od antiderivov funkcije f (x), enaka površini omejenega krivolinijskega trapeza z grafom funkcije y = f (x), z ravnimi črtami y = 0 , x = 9 in x = 5. Glede na graf ugotovimo, da je navedeni ukrivljeni trapez trapez z osnovama 4 in 3 ter višino 3.

Njeno območje je \ frac (4 + 3) (2) \ cdot 3 = 10,5.

Odgovori

Vir: »Matematika. Priprave na izpit 2017. Raven profila". Ed. FF Lysenko, S. Yu. Kulabukhova.

Stanje

Slika prikazuje graf y = f "(x) - odvod funkcije f (x), definiran na intervalu (-4; 10). Poiščite intervale padanja funkcije f (x). V odgovor, navedite dolžino največjega od njih.

Pokaži rešitev

Rešitev

Kot veste, funkcija f (x) pada na tistih intervalih, v vsaki točki katerih je izpeljanka f "(x) manjša od nič. Ob upoštevanju, da je treba najti dolžino največjega od njih, so trije takšni intervali se naravno razlikujejo od slike: (-4; -2) ; (0; 3); (5; 9).

Dolžina največjega od njih - (5; 9) je enaka 4.

Odgovori

Vir: »Matematika. Priprave na izpit 2017. Raven profila". Ed. FF Lysenko, S. Yu. Kulabukhova.

Stanje

Slika prikazuje graf y = f "(x) - izvod funkcije f (x), definirane na intervalu (-8; 7). Poiščite največje število točk funkcije f (x), ki pripadajo interval [-6; -2].

Pokaži rešitev

Rešitev

Graf kaže, da izpeljanka f "(x) funkcije f (x) spremeni predznak iz plusa v minus (na takih točkah bo maksimum) na točno eni točki (med -5 in -4) od interval [-6; -2]. Zato je na intervalu [-6; -2] natanko ena največja točka.

Odgovori

Vir: »Matematika. Priprave na izpit 2017. Raven profila". Ed. FF Lysenko, S. Yu. Kulabukhova.

Stanje

Slika prikazuje graf funkcije y = f (x), definirane na intervalu (-2; 8). Določite število točk, pri katerih je izvod funkcije f (x) 0.

Pokaži rešitev

Rešitev

Enakost odvoda v točki nič pomeni, da je tangenta na graf funkcije, narisana na tej točki, vzporedna z osjo Ox. Zato najdemo točke, pri katerih je tangenta na graf funkcije vzporedna z osjo Ox. Na tem grafikonu so takšne točke skrajne točke (točke maksimuma ali minimuma). Kot lahko vidite, obstaja 5 ekstremnih točk.

Odgovori

Vir: »Matematika. Priprave na izpit 2017. Raven profila". Ed. FF Lysenko, S. Yu. Kulabukhova.

Stanje

Premica y = -3x + 4 je vzporedna s tangento na graf funkcije y = -x ^ 2 + 5x-7. Poiščite absciso dotične točke.

Pokaži rešitev

Rešitev

Naklon ravne črte do grafa funkcije y = -x ^ 2 + 5x-7 na poljubni točki x_0 je enak y "(x_0). Toda y" = - 2x + 5, torej y "(x_0 ) = - 2x_0 + 5. Kotni koeficient premice y = -3x + 4, določen v pogoju, je enak -3. Vzporedne premice imajo enak naklon. Zato najdemo takšno vrednost x_0, da je = -2x_0 + 5 = -3.

Dobimo: x_0 = 4.

Odgovori

Vir: »Matematika. Priprave na izpit 2017. Raven profila". Ed. FF Lysenko, S. Yu. Kulabukhova.

Stanje

Slika prikazuje graf funkcije y = f (x), na abscisni osi pa so označene točke -6, -1, 1, 4. Na kateri od teh točk je vrednost izpeljanke najmanjša? To točko navedite v svojem odgovoru.

Mojstrski razred matematike

v 11. razredu

na to temo

"IZVEDENA FUNKCIJA

V NALOGAH UPORABE "

učitelj matematike

Martinenko E.N.

Študijsko leto 2017-2018

Namen mojstrskega razreda: razvijati sposobnosti učencevuporaba teoretičnega znanja na temo "Izpeljanka funkcije" za reševanje problemov enotnega državnega izpita.

Naloge

Izobraževalni:povzeti in sistematizirati znanje učencev o temi

"Izpeljanka funkcije", upoštevajte prototipe problemov USE na to temo, študentom omogočite, da preizkusijo svoje znanje pri samostojnem reševanju problemov.

Razvoj: spodbujati razvoj spomina, pozornosti, samospoštovanja in sposobnosti samokontrole; oblikovanje osnovnih ključnih kompetenc (primerjanje, jukstapozicija, razvrščanje predmetov, določanje ustreznih načinov za reševanje izobraževalnega problema na podlagi določenih algoritmov, sposobnost samostojnega delovanja v negotovosti, nadzora in vrednotenja svojih dejavnosti, iskanja in odpraviti vzroke za nastale težave).

Izobraževalni: promovirati:

Oblikovanje odgovornega odnosa do učenja med učenci;

razvijanje trajnega zanimanja za matematiko;

ustvarjanje pozitivne notranje motivacije za študij matematike.

Tehnologije: individualno diferencirano učenje, IKT.

Metode poučevanja: verbalno, vizualno, praktično, problematično.

Oblike dela: posamezno, frontalno, v parih.

Oprema in materiali za lekcijo:projektor, platno, računalnik, simulator(Priloga št. 1), predstavitev za lekcijo(Priloga št. 2), individualno - diferencirane kartice za samostojno delo v parih(Priloga št. 3), seznam internetnih strani, individualno diferencirane domače naloge(Priloga št. 4).

Razlaga za mojstrski razred.

Ta mojstrski razred poteka v 11. razredu za pripravo na enotni državni izpit. Namenjen je uporabi teoretičnega gradiva na temo "Izpeljanka funkcije" pri reševanju izpitnih nalog.

Trajanje mojstrskega razreda- 20 minut.

Struktura mojstrskega razreda

I. Organizacijski trenutek -1 min.

II.Sporočanje teme, cilji mojstrskega tečaja, motivacija izobraževalnih dejavnosti - 1 min.

III. Frontalno delo. Usposabljanje "Naloge št. 14 BAZA, št. 7 PROFIL enotnega državnega izpita". Analiza dela s simulatorjem - 7 min.

IV.Individualno – diferencirano delo v parih. Samostojno reševanje nalog št. 12. (PROFIL) Medsebojno preverjanje - 9 min. On-line testiranje (BAZA) Analiza rezultatov testov - 8 min

V. Preverjanje individualne domače naloge. -1 minuta.

Vi. Individualno - diferencirana domača naloga -1 min.

Vii. KONTROLNI TEST 20 MINUT (4 MOŽNOSTI)

Napredek mojstrskega razreda

jaz .Organiziranje časa.

II Komuniciranje teme, cilji mojstrskega razreda, motivacija izobraževalnih dejavnosti.

(Diapozitivi 1-2, Dodatek #2)

Tema naše lekcije je "Izvod funkcije v nalogah izpita". Vsi poznajo rek "Majhna tuljava, a draga". Ena od takih "tuljav" v matematiki je izpeljanka. Izpeljanka se uporablja pri reševanju številnih praktičnih problemov v matematiki, fiziki, kemiji, ekonomiji in drugih disciplinah. Omogoča vam, da probleme rešujete preprosto, lepo in zanimivo.

Tema »Izpeljanka« je predstavljena v nalogi št. 14 osnovne stopnje ter v nalogah profilne stopnje št. 7,12, 18 in enotnega državnega izpita.

Delali ste z dokumenti, ki urejajo strukturo in vsebino kontrolno-merilnega gradiva enotnega državnega izpita iz matematike 2018. Ugotovite, katera znanja in veščine potrebujete za uspešno reševanje nalog USE na temo »Izpeljanka«.

(Diapozitivi 3-4, Dodatek # 2)

Ali ste se naučili "Kodifikator vsebinskih elementov MATEMATIKE za pripravo kontrolnih merilnih materialov za enotni državni izpit",

"Kodifikator zahtev za stopnjo izobrazbe diplomantov", "Specifikacija kontrolno-mernih materialov", "Demonstracijska različica kontrolno-mernih materialov enotnega državnega izpita 2018" in izvedel kakšna znanja in veščine o funkciji in njeni izpeljanki so potrebna za uspešno reševanje nalog na temo »Izpeljanka«.

Nujno

• ZNATI

pravila za izračun izvedenih finančnih instrumentov;

izpeljanke osnovnih elementarnih funkcij;

geometrijski in fizični pomen izpeljanke;
enačba tangente na graf funkcije;
študij funkcije z uporabo izpeljanke.

• BITI SPOSOBEN

izvajati dejanja s funkcijami (opisati obnašanje in lastnosti funkcije glede na graf, poiskati njeno najvišjo in najnižjo vrednost).

• UPORABA

pridobljena znanja in veščine v praksi in vsakdanjem življenju.

Imate teoretično znanje o temi Izpeljanke. Danes bomoNAUČITE SE UPORABLJATI ZNANJE O IZVEDENI FUNKCIJI ZA REŠEVANJE PROBLEMOV UPORABE.(Diapozitiv 4, dodatek št. 2)

Ni za nič Aristotel je to rekel"UM NI SAMO V ZNANJU, TEM TUDI V SPOSOBNOSTI UPORABE ZNANJA V PRAKSI"(Diapozitiv 5, dodatek št. 2)

Na koncu ure se bomo vrnili k cilju naše lekcije in ugotovili, ali smo ga dosegli?

III ... Frontalno delo.Usposabljanje "Naloge št. 14 BAZA št. 7 PROFIL enotnega državnega izpita" ( Dodatek št. 1). Analiza dela s simulatorjem.

Izberi pravilen odgovor izmed štirih predlaganih.

Kakšna je po vašem mnenju težava pri dokončanju naloge #7?

Kaj menite, katere so tipične napake diplomantov na izpitu pri reševanju tega problema?

Ko odgovarjate na vprašanja naloge št. 14 BAZA IN št. 7 PROFIL, morate znati opisati obnašanje in lastnosti funkcije iz grafa odvoda, iz grafa funkcije pa obnašanje in lastnosti funkcije. izpeljanka funkcije. In to zahteva dobro teoretično znanje o naslednjih temah: »Geometrijski in mehanski pomen izpeljanke. Tangenta na graf funkcije. Uporaba izpeljanke za preučevanje funkcij.

Analizirajte, katere naloge so vam povzročale težave?

Katera teoretična vprašanja morate vedeti?

IV. On - line testiranje pri nalogah №14 (BAZA)Analiza rezultatov testov.

Spletno mesto za testiranje v lekciji:http://www.mathb-ege.sdamgia.ru/

Kdo ni naredil napak?

Kdo je imel težave pri testiranju? zakaj?

Pri katerih nalogah so bile storjene napake?

Zaključite, katera teoretična vprašanja morate vedeti?

Individualno – diferencirano delo v parih. Samostojna rešitev problemov №12. (PROFIL)Vzajemno preverjanje.(Priloga št. 3)

Zapomnite si algoritem za reševanje nalog №12 izpita za iskanje ekstremnih točk, ekstremov funkcije, največje in najmanjše vrednosti funkcije na intervalu z uporabo izpeljanke.

Rešite težave z izpeljanko

Študentje se soočajo s težavo:

"Pomislite, ali je mogoče nekatere probleme št. 12 rešiti na drugačen način, brez uporabe izpeljanke?"

1 par

2 para

3 pari

4 pari

(Učenci zagovarjajo svojo rešitev tako, da na tablo napišejo glavne korake za reševanje problemov. Učenci ponudijo dva načina reševanja problema #2).

Rešitev problema. Zaključek za študente:

"Nekatere naloge št. 12 izpita za iskanje najmanjše in največje vrednosti funkcije je mogoče rešiti brez uporabe izpeljanke, pri čemer se zanašamo na lastnosti funkcij."

Analizirajte, katero napako ste naredili pri nalogi?

Katera teoretična vprašanja morate ponoviti?

V. Preverjanje individualne domače naloge. (Diapozitivi 7-8, Dodatek št. 2)

Vegelman V. je dobil individualno domačo nalogo: iz priročnikov za pripravo na izpit št. 18.

(Študent poda rešitev problema, pri čemer se opira na funkcionalno-grafično metodo kot enega od načinov reševanja nalog št. 18 izpita in poda kratko razlago te metode).

Vii. Individualno - diferencirane domače naloge

(Diapozitiv 9, priloga št. 2), (Priloga št. 4).

Pripravila sem seznam spletnih strani za pripravo na izpit. Na teh spletnih mestih lahko opravite tudi spletno testiranje. Za naslednjo lekcijo morate: 1) pregledati teoretično gradivo na temo "Izpeljanka funkcije";

2) na spletnem mestu "Odprta banka nalog iz matematike" (http://mathege.ru/ ) poišči prototipe nalog št. 14 BAZA IN št. 7 in 12 PROFIL in reši vsaj 10 nalog PROFIL;

3) V. Vegelman, reši naloge s parametri (PRILOGA 4). naloge 1-8 (možnost 1).OSNOVNA RAVEN

VIII. Ocene lekcije.

Kako bi se ocenil za lekcijo?

Ali menite, da bi se lahko pri lekciji odrezali bolje?

IX. Povzetek lekcije. Odsev

Naj povzamemo naše delo. Kaj je bil namen lekcije? Ali menite, da je bilo doseženo?

Poglejte tablo in v enem stavku, z izbiro začetka besedne zveze, nadaljujte s stavkom, ki vam najbolj ustreza.

Čutila sem…

naučil sem se…

Uspelo mi je …

Bil sem zmožen ...

Bom poskusil …

To me je presenetilo …

hotel sem…

Ali lahko rečete, da ste med poukom obogatili vašo zalogo znanja?

Torej, ponovili ste teoretična vprašanja o izpeljanki funkcije, svoje znanje uporabili pri reševanju prototipov nalog UPORABE (št. 14 OSNOVNA STOPNJA št. 7,12 NIVO PROFILA), V. Vegelman pa je opravil nalogo št. s parametrom, ki je naloga povečane stopnje težavnosti.

V veselje mi je bilo delati z vami in upam, da boste znanje, pridobljeno pri pouku matematike, lahko uspešno uporabili ne le pri opravljanju enotnega državnega izpita, ampak tudi pri nadaljnjem študiju.

Učno uro bi rad zaključil z besedami italijanskega filozofaTomaž Akvinski"Znanje je tako dragocena stvar, da ga ni sramotno dobiti iz katerega koli vira."(Slide 10, Dodatek # 2).

Želim vam uspešno pripravo na izpit!

Predogled:

Če želite uporabiti predogled predstavitev, si ustvarite Google Račun (račun) in se prijavite vanj: https://accounts.google.com

Napisi diapozitivov:

Priprava na izpit SIMULATOR na temo "Izpeljanka" Naloga številka 14 osnovna raven, številka 7, profilna stopnja 12

f (x) f / (x) x Na sliki je prikazan graf izvoda funkcije y = f (x), določenega na intervalu (- 8; 8). Raziščimo lastnosti grafa in lahko bomo odgovorili na številna vprašanja o lastnostih funkcije, čeprav graf same funkcije ni predstavljen! y = f / (x) 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 4 3 2 1 -1 -2 -3 -4 -5 yx 6 3 0 -5 Najdi točke kjer je f / (x) = 0 (to so ničle funkcije). + - - + +

NALOGA številka 14 Osnovna raven matematike

Slika prikazuje graf funkcije y = f (x) in točke A, B, C in D so označene na osi Ox. Z uporabo grafa vsaki točki dodelite značilnosti funkcije in njenega izvoda. ABCD 1) vrednost funkcije v točki je negativna in vrednost izpeljanke funkcije v točki je pozitivna 2) vrednost funkcije v točki je pozitivna in vrednost odvoda funkcije na točki je negativna 3) vrednost funkcije v točki je negativna in vrednost izpeljanke funkcije v točki je negativna 4) vrednost funkcije v točki je pozitivna in vrednost izvod funkcije v točki je pozitiven

№ 1 Slika prikazuje graf funkcije y = f (x) in označene točke A, B, C in D na osi Ox. Z uporabo grafa vsaki točki dodelite značilnosti funkcije in njenega izvoda. 1) vrednost funkcije v točki je pozitivna in vrednost izpeljanke funkcije v točki je negativna 2) vrednost funkcije v točki je negativna in vrednost izpeljanke funkcije pri točka je negativna 3) vrednost funkcije v točki je pozitivna in vrednost izpeljanke funkcije v točki je pozitivna 4) vrednost funkcije v točki je negativna in vrednost izpeljanke funkcije v točki je pozitivna ABCD

Slika prikazuje graf funkcije y = f (x). Točke a, b, c, d in e določajo intervale na osi Ox. Z uporabo grafa vsakemu intervalu dodelite karakteristiko funkcije ali njenega izvoda. A) (a; b) B) (b; c) C) (c; d) D) (d; e) 1) vrednosti funkcije so pozitivne na vsaki točki intervala 2) vrednosti ​​izvoda funkcije so negativne na vsaki točki intervala 3) vrednosti izpeljanke funkcije so pozitivne na vsaki točki intervala 4) vrednosti funkcije so negativne na vsaki točki intervala

Slika prikazuje graf funkcije y = f (x). Številke a, b, c, d in e določajo intervale na osi Ox. Z uporabo grafa vsakemu intervalu dodelite karakteristiko funkcije ali njenega izvoda. A) (a; b) B) (b; c) C) (c; d) D) (d; e) 1) vrednosti funkcije so pozitivne na vsaki točki intervala 2) vrednosti ​​funkcije so negativne na vsaki točki intervala 3) vrednosti derivativnih funkcij so negativne na vsaki točki intervala 4) vrednosti izpeljanke funkcije so pozitivne na vsaki točki intervala

Na sliki je prikazan graf funkcije in nanjo narisane tangente v točkah z abscisami A, B, C in D. A B C D 1) - 1,5 2) 0,5 3) 2 4) - 0,3

Na sliki je prikazan graf funkcije in nanjo narisane tangente v točkah z abscisami A, B, C in D. A B C D 1) 23 2) - 12 3) - 113 4) 123

NALOGA številka 7 Matematični profilni nivo

Naloge za geometrijski pomen izpeljanke

1) Slika prikazuje graf funkcije y = f (x) in tangento nanjo v točki z absciso x 0. Poiščite vrednost odvoda v točki x 0. -2 -0,5 2 0,5 Pomisli! Pomislite! Prav! Pomislite! x 0 Geometrični pomen izpeljanke: k = tg α Kot naklona tangente na os Ox je topo, zato je k

5 11 8 2) Kontinuirana funkcija y = f (x) je nastavljena na interval (-6; 7). Slika prikazuje njen graf. Poišči število točk, pri katerih je tangenta na graf funkcije vzporedna z premico y = 6. Preverjanje y = f (x) y x 3 Pomisli! Pomislite! Pomislite! Prav! - 6 7 y = 6. Prelomna točka. Izpeljanka trenutno NE obstaja! О -4 3 5 1, 5

Naloge za določanje značilnosti funkcije iz grafa njenega izvoda

3) Slika prikazuje graf odvoda funkcije y = f / (x), podane na intervalu (- 6; 8). Preglejte funkcijo y = f (x) za ekstrem in navedite število njenih ekstremnih točk. 2 1 4 5 Narobe! Ni res! Prav! Ni res! Preverite (2) f (x) f / (x) -2 + - y = f / (x) 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 4 3 2 1 - 1 -2 -3 -4 -5 yx -5 + min max О

4 -3 -2 -1 1 2 3 4 5 x 5) Slika prikazuje graf odvoda funkcije, podane v intervalu [-5; 5]. Preverite monotonost funkcije in navedite največjo največjo točko. 3 2 4 5 Pomisli! Pomislite! Prav! Pomislite! y = f / (x) + + + - - О - f / (x) - + - + - + f (x) -4 -2 0 3 4 Od dveh največjih točk je največji x max = 3 max max y

7) Slika prikazuje graf odvoda funkcije. Poiščite dolžino naraščajočega intervala te funkcije. Preverite O -7 -6 -5 -4 -3 -2 -1 7 6 5 4 3 2 1 -1 -2 -3 -4 -5 -6 -7 4 2 3 5 RAZMISLITE! + RAZMISLITE! PRAV! RAZMISLITE! y x 3 y = f / (x)

4 -3 -2 -1 1 2 3 4 5 x 6) Slika prikazuje graf odvoda funkcije niza v intervalu [-5; 5]. Preverite monotonost funkcije y = f (x) in navedite število intervalov zmanjšanja. 3 2 4 1 Pomisli! Pomislite! Prav! Pomislite! y = f / (x) f (x) -4 -2 0 4 f / (x) - + - + - + + О - - - y

Naloge za določanje značilnosti grafične izpeljanke funkcije.

Slika prikazuje graf diferenciabilne funkcije y = f (x). Na abscisi je označenih devet točk: x 1, x 2, ..., x 9. Poišči vse označene točke, pri katerih je izvod funkcije f (x) negativen. V odgovoru navedite število teh točk.

Slika prikazuje graf funkcije y = f (x), definirane na intervalu (a; b). Določite število celih točk, pri katerih je izvod funkcije pozitiven. a) b) Odločite se sami! Rešitev. če se poveča. Celotne rešitve za: x = -2; x = -1; x = 5; x = 6. Njihovo število je 4. Celotne rešitve za: x = 2; x = 3; x = 4; x = 10; x = 11. Njihovo število je 5. Odgovor: 4. Odgovor: 5.

Težave za fizični pomen izpeljanke

Odgovor: 3 Odgovor: 14

NALOGA številka 12 Matematični profilni nivo

Samostojno delo v paru Naloga številka 12 Profilna stopnja

Predogled:

Dodatek 3 posamezne kartice št. 12

1. Poiščite največjo točko funkcije1 Poiščite minimalno točko funkcije

2. Poiščite največjo točko funkcije2 Poiščite minimalno točko funkcije

Linnik D. Vovnenko I

1. Poišči najmanjšo vrednost funkcije1. Poišči največjo vrednost funkcije na segmentu

na segmentu

Vegelman V.

A.

1. Poiščite največjo točko funkcije1. Poiščite minimalno točko funkcije

2. Poiščite najmanjšo vrednost funkcije2. Poišči največjo vrednost funkcije na segmentu

Na segmentu

Leontyeva A. Isaenko K.

IZVEN REVIZIJSKE PRAKSE 2

Pretvarjanje funkcijskih grafov.

Tarča

Z različnimi transformacijami sestavite grafe funkcij, odgovorite na vprašanje problema.

Zaključek dela

Metodična navodila

Delo je zasnovano za 10 variant, številka različice sovpada z zadnjo številko serijske številke na seznamu. Na primer, 1, 11, 21, 31 ... izvedite 1 možnost, 2,12, 22 ... - 2 možnosti itd.

Delo je sestavljeno iz dveh delov: prvi del naloge 1 - 5, to so naloge, ki jih je treba opraviti za pridobitev kredita, če so te naloge opravljene z napako, jih je treba popraviti in delo oddati še enkrat za preverjanje. Drugi del vsebuje naloge, z izpolnjevanjem katerih si lahko prislužite dodatno oceno: glavni del +2 nalogi - "4", glavni del +3 naloge - "5".

Naloga 1. Graf linearne funkcije je ravna črta, za izris sta dovolj dve točki. (vrednosti argumenta x vzamemo poljubno, vrednost funkcije y pa štejemo tako, da jo nadomestimo v formulo).

Če želite preveriti, ali graf funkcije poteka skozi določeno točko, morate namesto x in y nadomestiti koordinate točke, če dobite pravilno enakost, potem ravna črta poteka skozi določeno točko, sicer ne .

Naloga 2, 3, 4. Grafi določenih funkcij so pridobljeni iz grafov funkcij , s premikom vzdolž osi x ali y.

, najprej narišemo funkcijo oz , nato ga premaknemo za "a" enote v desno ali levo (+ a - v levo, - in v desno), nato ga premaknemo za "c" enote navzgor ali navzdol (+ b - gor, -b - dol)

Enako z drugimi funkcijami:

5. naloga Če želite narisati graf funkcije: , morate: 1) narisati funkcijo , 2) pustimo del grafa, ki je nad osjo x, nespremenjen, 3) zrcalimo del grafa, ki je pod x-osjo.

Naloge za samostojno rešitev.

Obvezni del

Naloga 1. Narišite graf linearne funkcije, ugotovite, ali gre graf funkcije skozi določeno točko:

Naloga 2. Narišite graf kvadratne funkcije, določite nabor vrednosti za to funkcijo.

Naloga 3. Zgradite graf funkcije, ugotovite, ali se navedena funkcija poveča ali zmanjša.

Naloga 4. Sestavite graf funkcije, odgovorite na vprašanje problema.

Naloga 5. Narišite graf funkcije, ki vsebuje znak modula.

Naloge za dodatno ocenjevanje.

Naloga 6. Narišite graf funkcije, dane po delih, ugotovite, ali obstaja prelomna točka za to funkcijo:

Naloga 7. Ugotovite, koliko rešitev ima sistem enačb, odgovor je utemeljiti. Z odgovori na vprašanja naredite zaključke.

Katere funkcije ste zarisali pri tem delu?

Kako se imenuje graf linearne funkcije?

Kako se imenuje graf kvadratne funkcije?

Katere transformacije grafov poznate?

Kako se graf sode funkcije nahaja v koordinatnem sistemu? Graf čudne funkcije?

Izvod funkcije $ y = f (x) $ v dani točki $ x_0 $ je meja razmerja prirastka funkcije in ustreznega prirastka njenega argumenta, pod pogojem, da se slednji nagiba k nič:

$ f "(x_0) = (lim) ↙ (△ x → 0) (△ f (x_0)) / (△ x) $

Diferenciacija je operacija iskanja izpeljanke.

Tabela izpeljank nekaterih osnovnih funkcij

Funkcija	Izpeljanka
$ c $	$0$
$ x $	$1$
$ x ^ n $	$ nx ^ (n-1) $
$ (1) / (x) $	$ - (1) / (x ^ 2) $
$ √x $	$ (1) / (2√x) $
$ e ^ x $	$ e ^ x $
$ lnx $	$ (1) / (x) $
$ sinx $	$ cosx $
$ cosx $	$ -sinx $
$ tgx $	$ (1) / (cos ^ 2x) $
$ ctgx $	$ - (1) / (greh ^ 2x) $

Osnovna pravila za razlikovanje

1. Odvod vsote (razlike) je enak vsoti (razliki) izpeljank

$ (f (x) ± g (x)) "= f" (x) ± g "(x) $

Poiščite izpeljavo funkcije $ f (x) = 3x ^ 5-cosx + (1) / (x) $

Odvod vsote (razlike) je enak vsoti (razliki) izpeljank.

$ f "(x) = (3x ^ 5)" - (cos x) "+ ((1) / (x))" = 15x ^ 4 + sinx - (1) / (x ^ 2) $

2. Izpeljanka dela

$ (f (x) g (x)) "= f" (x) g (x) + f (x) g (x) "$

Poiščite izpeljavo $ f (x) = 4x cosx $

$ f "(x) = (4x)" cosx + 4x (cosx) "= 4 cosx-4x sinx $

3. Izpeljanka količnika

$ ((f (x)) / (g (x))) "= (f" (x) g (x) -f (x) g (x) ") / (g ^ 2 (x)) $

Poiščite izpeljavo $ f (x) = (5x ^ 5) / (e ^ x) $

$ f "(x) = ((5x ^ 5)" e ^ x-5x ^ 5 (e ^ x) ") / ((e ^ x) ^ 2) = (25x ^ 4 e ^ x- 5x ^ 5 e ^ x) / ((e ^ x) ^ 2) $

4. Odvod kompleksne funkcije je enak zmnožku izvoda zunanje funkcije z odvodom notranje funkcije

$ f (g (x)) "= f" (g (x)) g "(x) $

$ f "(x) = cos" (5x) · (5x) "= - sin (5x) · 5 = -5sin (5x) $

Fizični pomen izpeljanke

Če se materialna točka giblje premočrtno in se njena koordinata spreminja glede na čas po zakonu $ x (t) $, je trenutna hitrost te točke enaka derivatu funkcije.

Točka se giblje vzdolž koordinatne črte po zakonu $ x (t) = 1,5t ^ 2-3t + 7 $, kjer je $ x (t) $ koordinata v času $ t $. V katerem trenutku bo hitrost točke enaka 12 $?

1. Hitrost je izpeljanka od $ x (t) $, zato najdemo izvod dane funkcije

$ v (t) = x "(t) = 1,5 · 2t -3 = 3t -3 $

2. Če želite ugotoviti, v katerem trenutku je bila hitrost $ t $ enaka $ 12 $, sestavite in rešite enačbo:

Geometrijski pomen izpeljanke

Spomnimo se, da lahko enačbo premice, ki ni vzporedna s koordinatnimi osmi, zapišemo v obliki $ y = kx + b $, kjer je $ k $ naklon premice. Koeficient $ k $ je enak tangentu nagibnega kota med premo črto in pozitivno smerjo osi $ Ox $.

Izvod funkcije $ f (x) $ v točki $ x_0 $ je enak naklonu $ k $ tangente na graf na tej točki:

Zato lahko sestavimo splošno enakost:

$ f "(x_0) = k = tgα $

Na sliki se tangenta na funkcijo $ f (x) $ poveča, zato se koeficient $ k> 0 $. Ker je $ k> 0 $, potem je $ f "(x_0) = tgα> 0 $. Kot $ α $ med tangento in pozitivno smerjo $ Ox $ je oster.

Na sliki se tangenta na funkcijo $ f (x) $ zmanjša, zato je koeficient $ k< 0$, следовательно, $f"(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.

Na sliki je tangenta na funkcijo $ f (x) $ vzporedna z osjo $ Ox $, zato je koeficient $ k = 0 $, torej $ f "(x_0) = tan α = 0 $. točka $ x_0 $, pri kateri je $ f "(x_0) = 0 $, klicana ekstremno.

Na sliki je prikazan graf funkcije $ y = f (x) $ in tangenta na ta graf, narisana v točki z absciso $ x_0 $. Poiščite vrednost izvoda funkcije $ f (x) $ v točki $ x_0 $.

Tangentna črta na graf se poveča, torej $ f "(x_0) = tg α> 0 $

Če želite najti $ f "(x_0) $, poiščite tangento nagibnega kota med tangento in pozitivno smerjo osi $ Ox $. To naredite tako, da trikotniku $ ABC $ dodate tangento.

Poiščite tangento kota $ BAC $. (Tangens ostrega kota v pravokotnem trikotniku je razmerje med nasprotno nogo in sosednjo nogo.)

$ tg BAC = (BC) / (AC) = (3) / (12) = (1) / (4) = 0,25 $

$ f "(x_0) = tg BAC = 0,25 $

Odgovor: 0,25 $

Izpeljanka se uporablja tudi za iskanje intervalov naraščajočih in padajočih funkcij:

Če je v intervalu $ f "(x)> 0 $, se funkcija $ f (x) $ v tem intervalu poveča.

Če $ f "(x)< 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.

Slika prikazuje graf funkcije $ y = f (x) $. Poiščite med točkami $ x_1, x_2, x_3… x_7 $ tiste točke, pri katerih je izpeljanka funkcije negativna.

V odgovor zapišite število danih točk.

V nalogi številka 13 USE iz matematike osnovne ravni boste morali pokazati spretnosti in znanje enega od konceptov obnašanja funkcije: izpeljank na točki ali stopnje naraščanja ali padanja. Teorija bo tej nalogi dodana nekoliko kasneje, vendar nam to ne preprečuje, da bi podrobno analizirali več tipičnih možnosti.

Analiza tipičnih možnosti za naloge št. 14 USE pri matematiki osnovne stopnje

Možnost 14MB1

Graf prikazuje odvisnost temperature od časa med segrevanjem motorja osebnega avtomobila. Vodoravna os prikazuje čas v minutah, ki je pretekel od zagona motorja; navpična os je temperatura motorja v stopinjah Celzija.

Z uporabo grafa vsakemu časovnemu intervalu dodelite značilnost procesa ogrevanja motorja v tem intervalu.

V tabeli pod vsako črko navedite ustrezno številko.

Izvedbeni algoritem:

1. Izberite časovni interval, v katerem je temperatura padla.
2. Nanesite ravnilo na 30 ° C in določite časovni interval, v katerem je bila temperatura pod 30 ° C.

rešitev:

Izberemo časovni interval, v katerem je temperatura padla. To območje je vidno s prostim očesom, začne se 8 minut po zagonu motorja.

Nanesite ravnilo na 30 °C in določite časovni interval, v katerem je bila temperatura pod 30 °C.

Pod ravnilom bo odsek, ki ustreza časovnemu intervalu 0 - 1 min.

S svinčnikom in ravnilom bomo ugotovili, v katerem časovnem intervalu je bila temperatura v območju od 40 ° C do 80 ° C.

Na grafu izpustimo navpičnice iz točk, ki ustrezata 40°C in 80°C, iz dobljenih točk pa izpustimo navpičnice na časovno os.

Vidimo, da ta temperaturni interval ustreza časovnemu intervalu 3 - 6,5 minute. To je od tistih, danih v stanju 3 - 6 minut.

Za izbiro manjkajočega odgovora uporabimo metodo izločanja.

Možnost 14MB2

rešitev:

Analizirajmo graf funkcije A. Če se funkcija povečuje, je izvod pozitiven in obratno. Derivat funkcije je enak nič na točkah ekstrema.

Najprej se poveča funkcija A, t.j. izpeljanka je pozitivna. To ustreza grafoma izpeljank 2 in 3. Na najvišji točki funkcije x = -2, torej na tej točki mora biti izvod nič. Ta pogoj izpolnjuje graf številka 3.

Najprej se zmanjša funkcija B, t.j. izpeljanka je negativna. To ustreza grafoma izpeljank 1 in 4. Največja točka funkcije je x = -2, to pomeni, da mora biti na tej točki izpeljanka enaka nič. Ta pogoj izpolnjuje graf številka 4.

Najprej se poveča funkcija B, t.j. izpeljanka je pozitivna. To ustreza grafoma izpeljank 2 in 3. Največja točka funkcije x = 1, to pomeni, da mora biti izpeljanka na tej točki enaka nič. Ta pogoj je izpolnjen z grafom številka 2.

Z metodo eliminacije lahko ugotovimo, da graf funkcije Γ ustreza grafu odvoda pri številki 1.

Odgovor: 3421.

Možnost 14MB3

Algoritem izvedbe za vsako od funkcij:

1. Določite intervale naraščajočih in padajočih funkcij.
2. Določite največjo in najmanjšo točko funkcij.
3. Pripravite zaključke, uskladite predlagane urnike.

rešitev:

Analizirajmo graf funkcije A.

Če se funkcija povečuje, je izpeljanka pozitivna in obratno. Derivat funkcije je enak nič na točkah ekstrema.

Točka ekstrema je točka, na kateri je dosežena največja ali najmanjša vrednost funkcije.

Najprej se poveča funkcija A, t.j. izpeljanka je pozitivna. To ustreza grafoma izpeljank 3 in 4. Na najvišji točki funkcije x = 0, torej na tej točki mora biti izpeljanka enaka nič. Ta pogoj izpolnjuje graf številka 4.

Analizirajmo graf funkcije B.

Najprej se zmanjša funkcija B, t.j. izpeljanka je negativna. To ustreza grafoma izpeljank 1 in 2. Minimalna točka funkcije je x = -1, to pomeni, da mora biti izpeljanka na tej točki enaka nič. Ta pogoj je izpolnjen z grafom številka 2.

Analizirajmo graf funkcije B.

Najprej se zmanjša funkcija B, t.j. izpeljanka je negativna. To ustreza grafoma izpeljank 1 in 2. Minimalna točka funkcije x = 0, to pomeni, da mora biti izpeljanka na tej točki enaka nič. Ta pogoj je izpolnjen z grafom številka 1.

Z metodo eliminacije lahko ugotovimo, da graf funkcije Γ ustreza grafu odvoda pri številki 3.

Odgovor: 4213.

Možnost 14MB4

Na sliki je prikazan graf funkcije in nanjo narisane tangente v točkah z abscisami A, B, C in D.Desni stolpec prikazuje vrednosti odvoda v točkah A, B, C in D. Z uporabo grafa vsaki točki dodelite vrednost izpeljanke funkcije v njej.

TOČKE
A
V
Z
D

VREDNOSTI IZVODA
1) –4
2) 3
3) 2/3
4) -1/2

Spomnimo se, kaj pomeni izpeljanka, in sicer njeno vrednost na točki - vrednost odvodne funkcije v točki je enaka tangentu naklona (koeficientu) tangente.

V odgovorih imamo dve pozitivni in dve negativni možnosti. Kot se spomnimo, če je koeficient ravne črte (grafika y = kx + b) pozitiven, potem se premica poveča, če je negativna, potem se premica zmanjša.

Imamo dve naraščajoči ravni črti - v točkah A in D. Zdaj se spomnimo, kaj pomeni vrednost koeficienta k?

Koeficient k kaže, kako hitro se funkcija povečuje ali zmanjšuje (pravzaprav je koeficient k sam izpeljanka funkcije y = kx + b).

Zato k = 2/3 ustreza ravni črti - D, k = 3 - A.

Podobno v primeru negativnih vrednosti: točka B ustreza bolj strmi ravni črti s k = - 4, točka C - -1/2.

Možnost 14MB5

Na sliki je s pikami prikazana mesečna prodaja grelnikov v trgovini z gospodinjskimi aparati. Meseci so prikazani vodoravno, število prodanih grelnikov pa navpično. Zaradi jasnosti so točke povezane s črto.

S pomočjo slike povežite vsako od navedenih časovnih obdobij s prodajno značilnostjo grelnikov.

Algoritem izvajanja

Analiziramo dele grafa, ki ustrezajo različnim letnim časom. Formuliramo situacije, prikazane na grafikonu. Zanje najdemo najprimernejše možnosti odgovora.

rešitev:

Pozimi je število prodaj preseglo 120 kosov / mesec in se je nenehno povečevalo. Ta situacija ustreza odgovoru številka 3. tiste. dobimo: A – 3.

Spomladi je prodaja postopoma padla s 120 grelnikov na mesec na 50. Možnost 2 je najbližja temu besedilu. Imamo: B – 2.

Poleti se število prodaj ni spremenilo in je bilo minimalno. Drugi del tega besedila se v odgovorih ne odraža, za prvega pa je primeren le # 4. Zato imamo: NA 4.

Jeseni je prodaja rasla, vendar njihovo število v nobenem od mesecev ni preseglo 100 enot. Ta situacija je opisana v možnosti # 1. Dobimo: G – 1.

Možnost 14MB6

Graf prikazuje odvisnost hitrosti običajnega avtobusa od časa. Na navpični osi je hitrost avtobusa označena v km / h, na vodoravni osi - čas v minutah od začetka gibanja avtobusa.

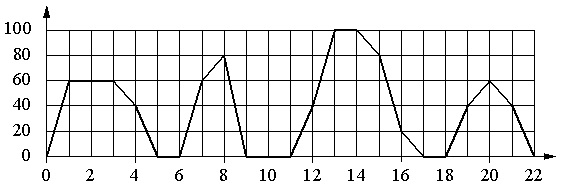
Z uporabo grafa vsakemu časovnemu intervalu dodelite značilnost gibanja vodila v tem intervalu.

Algoritem izvajanja

1. Določite ceno delitve na vodoravni in navpični lestvici.
2. Po vrsti analiziramo predlagane trditve 1–4 iz desnega stolpca ("Karakteristike"). Primerjamo jih s časovnimi intervali iz levega stolpca tabele, najdemo pare »črka-številka« za odgovor.

rešitev:

Delitev na vodoravni lestvici je 1 s, navpična pa 20 km / h.

1. Ko se avtobus ustavi, je njegova hitrost 0. Avtobus je imel ničelno hitrost 2 minuti zapored le od 9. do 11. minute. Ta čas je v intervalu 8–12 minut. Torej, imamo par za odgovor: B – 1.
2. Avtobus je imel v več časovnih intervalih hitrost 20 km/h in več. Poleg tega možnost A tukaj ni primerna, ker je bila na primer v 7. minuti hitrost 60 km / h, možnost B - ker je že bila uporabljena, možnost D - ker je na začetku in koncu intervala avtobus imel nič hitrosti... V tem primeru je primerna možnost B (12–16 min); v tem intervalu se avtobus začne premikati s hitrostjo 40 km / h, nato pospeši do 100 km / m in nato postopoma zmanjša hitrost na 20 km / h. Torej imamo: V 2.
3. Omejitev hitrosti je nastavljena tukaj. Hkrati ne upoštevamo možnosti B in C. Preostala intervala A in D sta primerna. Zato bi bilo pravilno najprej razmisliti o 4. možnosti in se nato spet vrniti na 3.
4. Od preostalih dveh intervalov je za karakteristiko št. 4 primernih le 4–8 minut, saj je v tem intervalu (v 6. minuti) prišlo do postanka. V intervalu 18-22 minut ni bilo postankov. Dobimo: A – 4... Iz tega sledi, da je za karakteristiko št. 3 treba vzeti interval Г, t.j. izkaže se par G – 3.

Možnost 14MB7

Pikčasta številka prikazuje povečanje prebivalstva Kitajske od leta 2004 do 2013. Horizontalno označuje leto, navpično - rast prebivalstva v odstotkih (povečanje prebivalstva glede na lansko leto). Zaradi jasnosti so točke povezane s črto.

S pomočjo slike povežite vsako od navedenih časovnih obdobij z značilnostmi rasti prebivalstva Kitajske v tem obdobju..

Algoritem izvajanja

1. Določite ceno delitve navpične lestvice slike. Najdemo ga kot razliko med parom sosednjih vrednosti lestvice, deljeno z 2 (ker sta dve sosednji vrednosti 2 delitvi).
2. Zaporedoma analiziramo značilnosti 1–4, podane v pogoju (levi stolpec tabele). Vsako od njih primerjamo z določenim časovnim obdobjem (desni stolpec tabele).

rešitev:

Navpična delitev lestvice je 0,01%.

1. Upadanje rasti se je nadaljevalo neprekinjeno od leta 2004 do 2010. V letih 2010–2011 je bila rast stabilno minimalna, od leta 2012 pa se je začela povečevati. tiste. rast se je leta 2010 ustavila. Letošnje leto je v obdobju 2009–2011. V skladu s tem imamo: V 1.
2. Najbolj strmo padajočo črto grafikona na sliki je treba šteti za največji padec rasti. Spada v obdobje 2006-2007. in je 0,04 % na leto (0,59-0,56 = 0,04 % v letu 2006 in 0,56-0,52 = 0,04 % v letu 2007). Od tu dobimo: A – 2.
3. Rast, navedena v karakteristiki št. 3, se je začela v letu 2007, nadaljevala v letu 2008 in končala v letu 2009. To ustreza časovnemu obdobju B, tj. imamo: B – 3.
4. Rast prebivalstva se je začela povečevati po letu 2011, t.j. v letih 2012–2013 Zato dobimo: G-4.

Možnost 14MB8

Na sliki je prikazan graf funkcije in nanjo narisane tangente v točkah z abscisami A, B, C in D.

Desni stolpec prikazuje vrednosti izpeljanke funkcije v točkah A, B, C in D. Z uporabo grafa vsaki točki dodelite vrednost izpeljanke funkcije v njej.

Algoritem izvajanja

1. Razmislite o paru tangent, ki imajo ostri kot s pozitivno smerjo abscisne osi. Primerjamo jih, najdemo ujemanje med parom ustreznih vrednosti izpeljank.
2. Razmislite o paru tangent, ki tvorijo topel kot s pozitivno smerjo abscisne osi. Primerjamo jih v absolutni vrednosti, določimo njihovo ujemanje z vrednostmi izpeljank med dvema preostalima v desnem stolpcu.

rešitev:

Akutni kot s pozitivno smerjo abscisne osi tvorijo izpeljanke v točki B in točki C. Ti derivati ​​imajo pozitivne vrednosti. Zato bi morali tukaj izbrati med vrednostma št. 1 in 3. Z uporabo pravila, da če je kot manjši od 45 0, je izvod manjši od 1, in če je več, potem več kot 1, sklepamo: v točki B je izpeljanka po modulu večja od 1, v točki C - manjša od 1. To pomeni, da lahko sestavite pare za odgovor: NA 3 in С – 1.

Odvodnici v točki A in točki D tvorita topel kot s pozitivno smerjo abscise. In tukaj uporabimo isto pravilo, ki ga nekoliko parafraziramo: bolj ko je tangenta na točki "pritiskana" na črto abscisne osi (na njeno negativno smer), večja je v absolutni vrednosti. Nato dobimo: izpeljanka v točki A je po absolutni vrednosti manjša od izpeljanke v točki D. Zato imamo pare za odgovor: A – 2 in D – 4.

Možnost 14MB9

Na sliki pike prikazujejo povprečno dnevno temperaturo zraka v Moskvi januarja 2011. Vodoravno označuje dan v mesecu, navpično - temperaturo v stopinjah Celzija. Zaradi jasnosti so točke povezane s črto.

S pomočjo slike povežite vsako od navedenih časovnih obdobij z značilnostjo spremembe temperature.

Algoritem izvajanja

Zaporedoma analiziramo značilnosti 1-4 (desni stolpec) z uporabo grafa na sliki. Vsako od njih postavimo v korespondenco z določenim časovnim obdobjem (levi stolpec).

rešitev:

1. Povišanje temperature smo opazili šele ob koncu obdobja 22.–28. januarja. Tu se je 27. in 28. povečala za 1 oziroma 2 stopinji. Ob koncu obdobja 1.–7. januarja je bila temperatura stabilna (–10 stopinj), konec januarja 8–14 in 15–21 januarja se je znižala (od –1 do –2 in od –11 do – 12 stopinj oziroma). Zato dobimo: G – 1.
2. Ker vsako časovno obdobje zajema 7 dni, je treba temperaturo analizirati od 4. dne vsakega obdobja. Temperatura je ostala nespremenjena 3-4 dni le od 4. do 7. januarja. Zato dobimo odgovor: A – 2.
3. Najnižja mesečna temperatura je bila opažena 17. januarja. Ta številka je v obdobju 15-21 januarja. Od tu imamo par: NA 3.
4. Temperaturni maksimum je padel 10. januarja in je znašal +1 stopinjo. Ta datum je med 8. in 14. januarjem. Zato imamo: B – 4.

Možnost 14MB10

Algoritem izvajanja

1. Vrednost funkcije v točki je pozitivna, če se ta točka nahaja nad osjo Ox.
2. Izvod v točki je večji od nič, če tangenta na to točko tvori ostri kot s pozitivno smerjo osi Ox.

rešitev:

Točka A. Je pod osjo Ox, kar pomeni, da je vrednost funkcije v njej negativna. Če vanj narišete tangento, bo kot med njo in pozitivno smerjo Ox približno 90 0, t.j. tvori oster kot. Torej je v tem primeru primerna značilnost številka 3. tiste. imamo: A – 3.

Točka B. Nahaja se nad osjo Ox, t.j. točka ima pozitivno vrednost funkcije. Tangentna črta na tej točki bo precej blizu osi abscise in s svojo pozitivno smerjo tvori tup kot (malo manj kot 180 0). V skladu s tem je izpeljanka na tej točki negativna. Tako je tukaj primerna značilnost 1. Dobimo odgovor: V 1.

Točka C. Točka se nahaja pod osjo Ox, tangenta v njej tvori velik topo kot s pozitivno smerjo abscisne osi. tiste. v točki C je vrednost tako funkcije kot izvoda negativna, kar ustreza karakteristiki št. 2. odgovor: C – 2.

Točka D. Točka je nad osjo Ox, tangenta v njej pa tvori ostri kot s pozitivno smerjo osi. To nakazuje, da sta tako vrednost funkcije kot vrednost izpeljanke tukaj večji od nič. odgovor: D – 4.

Možnost 14MB11

Na sliki je s pikami prikazana mesečna prodaja hladilnikov v trgovini z gospodinjskimi aparati. Meseci so prikazani vodoravno, število prodanih hladilnikov pa navpično. Zaradi jasnosti so točke povezane s črto.

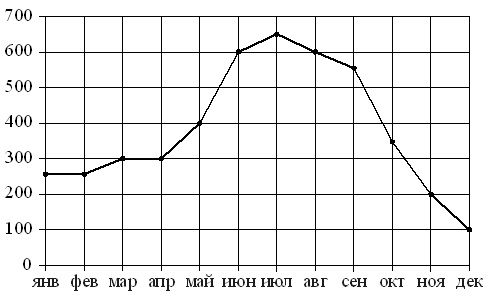
S pomočjo slike povežite vsako od navedenih časovnih obdobij s prodajno značilnostjo hladilnikov..