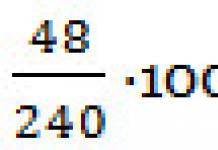klasa: 5
U ovom članku ćemo pogledati jednu od lekcija iz kursa matematike 5. razreda, posvećenu uvođenju kombinatorike.
Ciljevi lekcije.
Obrazovni:
Upoznati učenike sa novom vrstom problema (kombinatorni problemi), metodama za njihovo rješavanje - nabrajanje mogućih opcija, konstruisanje stabla mogućih opcija, primjena pravila množenja;
Uvesti novi koncept - faktorijal, konsolidovati ga prilikom rješavanja zadataka, primjera, jednačina.
Obrazovni:
Formiranje poštovanja prema drugovima, sposobnost slušanja i slušanja sagovornika
Formiranje stava prema prijateljstvu kao jednoj od najvažnijih ljudskih vrijednosti.
Razvojni:
Formiranje interesovanja za predmet;
Formiranje računarskih vještina;
Razvoj logičkog mišljenja;
Razvijanje sposobnosti da se dokaže i potkrijepi svoje mišljenje.
Tokom nastave
1. Organizacioni momenat
Učitelj: Danas imamo neobičnu lekciju. Rješavat ćemo zadatke koji se odnose na jednu od najzanimljivijih grana matematike - kombinatoriku. U nauci i stvarnom životu, vrlo često moramo rješavati probleme, čije je glavno pitanje pitanje „Na koliko načina se to može učiniti?“ Na primjer:
Na koliko načina možete ocijeniti učenika na času?
Na koliko načina možete dodijeliti monitor klase?
Na koliko načina možete dodijeliti dva polaznika učionice?
Prilikom rješavanja takvih zadataka morate napraviti različite kombinacije od konačnog broja elemenata i prebrojati broj kombinacija. Takvi problemi se nazivaju kombinatoričkim problemima, a grana matematike u kojoj se takvi problemi razmatraju naziva se kombinatorika. Kojoj još temi će lekcija biti posvećena saznaćete kada proverimo kako ste uradili domaći zadatak.
2. Provjera popunjenosti domaće zadaće
(U prethodnoj lekciji domaća zadaća je sastavljena tako da ima tačno 6 zadataka. Na primjer, u udžbeniku Vilenkin N.Ya. et al. to bi mogao biti br. 693(a,c), 735(1 ), 765 (a, b, V))
Na tabli se nalazi sto i karte pričvršćene magnetima. Na karticama na jednoj strani je odgovor na domaći zadatak, na drugoj je slovo.
Učitelj: Hajde da provjerimo tvoj domaći zadatak. Otvorite sveske i uzmite olovke. Pronađite odgovore na brojeve domaćih zadataka.
Učenici jedan po jedan izlaze na ploču, biraju karticu sa odgovorom i prilažu je u ćeliju tabele ispod broja zadatka. Najprije se kartice učvršćuju u ćelije tabele sa stranom na kojoj je napisan odgovor, tako da učenici mogu provjeriti ispravnost domaće zadaće. Ostali provjeravaju svoje odgovore u svojim sveskama.
| Vježba br. | 693(a) | 693(c) | 735(1) | 765(a) | 765(b) | 765(c) |
| Odgovori | 25 | 13 | 6 | 182 000 | 6 300 | 65 000 |
Opcije odgovora (nalaze se na različitim stranama kartica). Namjerno je prevelik broj kartica, tako da su neki od odgovora netačni.
| d | R | at | i | b | A | m | P | O |
| 25 | 13 | 6 | 182 000 | 6 300 | 65 000 | 49 | 12 | 18 200 |
“5” - ako je sve ispravno
“4” - ako je jedna greška
“3” - 2-3 greške
“2” - više od 3 greške
Učitelj: Hajde da okrenemo karte, koju si reč dobio? (PRIJATELJSTVO). Zaista, danas u lekciji nećemo samo rješavati matematičke probleme, poboljšati vještine računanja, već ćemo razgovarati i o prijateljstvu.
3. Novi materijal.
Učitelj: Dakle, već smo rekli da ćemo danas naučiti rješavati probleme, čije je glavno pitanje pitanje „Na koliko načina...“.
Postoje tri riječi “PRIJATELJSTVO”, “BIZNIS”, “LJUBAVI” (izrežite komade papira sa ovim riječima - 7 kartica za svaku riječ). Na koliko načina se ove riječi mogu koristiti za formiranje fraze?
Učenici nude opcije, te su opcije napisane na tabli.
Odgovor: 6 načina.
Učitelj: Koja je opcija po vašem mišljenju ispravna sa stanovišta ruskog jezika? (Prijateljstvo voli posao). Kako razumete ovu izjavu?
Učitelj: Ovdje je bilo kompletno nabrajanje svih mogućih opcija, ili, kako se obično kaže, svih mogućih kombinacija. Dakle, ovo je kombinatorni problem. Razmislimo o tome kako možemo zapisati i formalizirati rješenje ovog problema.
1 način. Označimo predložene riječi velikim slovima:
PRIJATELJSTVO – D
VOLI – L
DELO – E (uzmimo drugo slovo ove riječi)
Tada se sve metode koje ste nazvali mogu jednostavno navesti: DLE, DEL, LDE, ICE, EDL, ELD.
Ispostavilo se da se rješenje može formulirati u obliku modela koji se naziva stablo mogućih opcija. Prvo, to je jasno, kao i svaka slika, i, drugo, omogućava vam da sve uzmete u obzir, a da ništa ne propustite,
Učenici, pod vodstvom nastavnika, sastavljaju dijagram:
Metoda 3 (rezonovanje)
Jedna od tri riječi može biti prva: PRIJATELJSTVO, LJUBAVI, POSAO. Ako se izabere prva riječ, onda drugo mjesto može biti jedna od dvije preostale riječi, a treće mjesto može imati samo jednu preostalu riječ. Dakle, ukupne opcije su: .
Imajte na umu da se zadnja tehnika zove pravilo množenja.
Svaka od ove tri metode ima svoje prednosti i nedostatke (razgovarajte) Izbor rješenja je vaš! Zapazimo, međutim, da nam pravilo množenja omogućava rješavanje velikog broja problema u jednom koraku.
Anya ima 3 prijatelja, i svakom je kupila čokoladicu i želi im ih pokloniti za praznik. Na koliko načina ona to može učiniti?
Rješenje: Učenici izvode rješenje na tabli (rešenje se izvodi na 3 načina)
U društvu prijatelja je 6 ljudi: Andrey, Boris, Vitya, Grisha, Dima, Egor. U školskoj menzi ima 6 stolica za stolom. Prijatelji su odlučili da svaki dan različito sjede na ovih 6 stolica dok doručkuju. Koliko puta to mogu učiniti bez ponavljanja?
Učitelj: Koju metodu ćemo izabrati? (Učenici, pod vodstvom nastavnika, treba da dođu do zaključka da je ovo treći način – pravilo množenja).
Učenik crta rješenje na tabli.
Radi lakšeg rasuđivanja, pretpostavićemo da prijatelji sjedaju za stolom jedan po jedan. Pretpostavićemo da je Andrej prvi koji će sesti za sto. Ima 6 opcija stolica. Boris je drugi koji sjeda i samostalno bira stolicu od 5 preostalih. Vitya bira treći i imaće 4 stolice na izbor. Grisha će već imati 3 opcije, Dima – 2, Egor – 1. Prema pravilu množenja dobijamo:
Odgovor je 720 dana ili skoro 2 godine.
Učitelj: Kao što vidimo, uslovi problema su različiti, ali su rješenja u suštini ista. Stoga je zgodno uvesti istu notaciju za ove odgovore.
Definicija: proizvod svih prirodnih brojeva od 1 do n uključujući i naziva se n - faktorijal i označava se simbolom n!
Potpiši P! glasi “En factorial”, što u doslovnom prijevodu sa engleskog znači “sastoji se od P množitelji.” Napomenimo važnu karakteristiku ove vrijednosti – njen brzi rast.
Izračunati:
a) 1!; b) 2!; u 3!; d) 4!; e) 5!; e)10!
Oni misle da je 0! =1 (piši)
Zadatak 5.
Učitelj: PRIJATELJSTVO je jedno od najvažnijih bogatstava koje osoba može imati. Nije uzalud da se o prijateljstvu komponuju pjesme i pjesme, pišu poslovice i izreke. Koje poslovice i izreke o prijateljstvu znate?
Prijatelj u nevolji je zaista prijatelj.
Nemojte imati sto rubalja, ali imajte sto prijatelja.
Sigurnost je u brojkama.
Umri sam, ali pomozi svom drugu.
Stari prijatelj je bolji od dva nova.
Život je težak bez prijatelja.
Dobro urađeno! Za svaku osobu je veoma važno da ima dobre, prave prijatelje. Hajde da riješimo nekoliko primjera koristeći novi koncept - faktorijal i naučimo novu poslovicu o prijateljstvu.
| 7!+ | 8! – (13 - 5) 2 | 6! – 5! | ||
Kartice sa odgovorima se popunjavaju sa rezervom (postoje kartice sa brojevima koji nisu odgovori).
Tabela nakon popunjavanja:
| 7!+ | 8! – (13 - 5) 2 | 6! – 5! | ||
| 5048 | 40256 | 600 | 24 | 7 |
| br | prijatelj - | tražiti | ali pronašao - | čuvaj se |
Zadatak 6.
4 prijatelja su došla u posjetu Vasyu, i oni će pogledati novi film. Vasja ima stolicu u svojoj sobi, a doneo je i 4 stolice iz kuhinje. On će nesumnjivo sam zauzeti stolicu i posaditi svoje prijatelje na stolice. Vasja je izračunao da svoje prijatelje može smjestiti na 24 načina.
Učitelj: Da li je Vasja ispravno izračunao? (Da, sa matematičke tačke gledišta)
Da li je dobro prošao? (Razgovara se o moralnom aspektu problema)
4. Trenutak fizičkog vaspitanja.
Učitelj: Hajde da se odmorimo malo, a za to ćemo na minutu odraditi fizičku vježbu. Ako sam dobro pročitao izraz, onda ustaneš i podigneš ruke uvis, a ako je pogrešno, sjedneš sa rukama pored sebe.
Ustali smo. Počnimo, budite oprezni.
| Izraz | Reči učitelja | Tačno Netačno |
| 5! +3 | Iznos 5! i 3 | + |
| 2 – 7! | Proizvod od 2 i 7! | - |
| 4x: 2! | Privatno 4x i 2! | + |
| 5! + 7! + 3! | Zbir 5!, 7! i 3! | + |
| 20! - 19! | Privatni 20! i 19! | - |
6. Samostalan rad.
Učitelj: Pa, sad kad smo se dobro odmorili, hajde da proverimo šta smo danas naučili da radimo na času. Da bismo to učinili, mi ćemo raditi svoj vlastiti posao.
| Opcija 1 | Opcija 2 |
| 1. U 5. razredu srijedom ima 5 časova: matematika, ruski jezik, književnost, muzika i rad. Koliko opcija dnevnog rasporeda možete kreirati? | 1. Šest različitih pisama stavljeno je u 6 različitih koverti. Koliko postoji načina da se ovako razvije? |
| 2. Izračunajte: a) 6! – 2; b) 4! + (2+3) 2 |
2. Izračunajte: a) 3 2 + 5! b) (9-4) 2 + 4! |
| 3. Na koliko načina 5 dječaka može stati u red na blagajni ako je Tolya i dalje prvi? | 3. Na koliko načina Daša može da jede ručak koji se sastoji od prvog, drugog, trećeg i kolača ako će svakako prva pojesti tortu? |
7. Domaći.
Osmislite, zapišite uslove i rješenja 2 kombinatorna zadatka na temu „Porodica“. Crtajte na A4 listovima, možete napraviti crteže za zadatke.
8. Sažetak lekcije.
Hajde da rezimiramo lekciju.
Šta ste novo naučili? (Primili smo pravilo množenja, ispitali njegov geometrijski model - stablo opcija, uveli novi koncept - faktorijal)
šta ti se svidjelo?
čega se sjećaš?
Ocjene na nastavi.
književnost:
- E.A. Bunimović, V.A. Bulychev. Vjerovatnoća i statistika u predmetu matematike opšteobrazovne škole: predavanja 1-4, 5 – 8. – M.: Pedagoški univerzitet “Prvi septembar”, 2006.
- Vilenkin N.Ya. Matematika. 5. razred: udžbenik za opšte obrazovanje. institucije / N. Ya. Vilenkin i drugi - M.: Mnemosyna, 2009.
- Smykalova E.V. Dodatna poglavlja iz matematike za učenike 5. razreda. SPb: SMIO. Press, 2006.
- Mordkovich A.G. Događaji. Vjerovatnoće. Statistička obrada podataka: Dodatno. Paragrafi za kurs algebre 7-9 razred. obrazovne ustanove / A.G. Mordkovich, P.V. Semenov. – M.: Mnemosyne, 2006.
Prilikom rješavanja mnogih praktičnih zadataka potrebno je koristiti kombinacije elemenata, odabrati iz zadanog skupa one koji imaju određena svojstva i postaviti ih određenim redoslijedom. Takvi zadaci se zovu kombinatorski. Grana matematike koja se bavi rješavanjem problema izbora i rasporeda elemenata u skladu sa datim uslovima naziva se kombinatorika. Izraz "kombinatorika" dolazi od latinske riječi "kombina", što u prevodu na ruski znači „kombinovati“, „spojiti“.
Odabrane grupe elemenata nazivaju se veze. Ako su svi elementi veze različiti, tada dobivamo veze bez ponavljanja, što ćemo razmotriti u nastavku.
Većina kombinatornih problema rješava se korištenjem dva osnovna pravila - pravila zbroja i pravila proizvoda.
Zadatak 1.
Trgovina Sve za čaj ima 6 različitih šoljica i 4 različita tanjira. Koliko opcija šoljica i tanjurića možete kupiti?
Rješenje.
Šoljicu možemo izabrati na 6 načina, a tanjirić na 4 načina. Pošto moramo kupiti par šoljica i tanjurića, to se može uraditi na 6 · 4 = 24 načina (prema pravilu proizvoda).
Odgovor: 24.
Da biste uspješno riješili kombinatorne probleme, također morate odabrati pravu formulu koju ćete koristiti za pronalaženje broja potrebnih spojeva. Sljedeći dijagram će vam pomoći u tome. 
Razmotrimo rješavanje nekoliko problema za različite vrste veza bez ponavljanja.
Zadatak 2.
Pronađite broj trocifrenih brojeva koji se mogu sastaviti od brojeva 1, 2, 3, 4, 5, 6, 7, ako se brojevi ne mogu ponoviti u broju.
Rješenje.
Da bismo odabrali formulu, saznajemo da se za brojeve koje ćemo sastaviti uzima u obzir redoslijed i ne biraju se svi elementi u isto vrijeme. To znači da je ova veza raspored od 7 elemenata po 3. Koristimo formulu za broj plasmana: A 7 3 = 7(7 – 1)(7 – 2) = 7 · 6 · 5 = 210 brojeva.
Odgovor: 210.
Zadatak 3.
Koliko ima sedmocifrenih telefonskih brojeva u kojima su sve cifre različite i broj ne može početi nulom?
Rješenje.
Na prvi pogled, ovaj zadatak je isti kao i prethodni, ali je poteškoća u tome što ne smijemo uzeti u obzir one veze koje počinju od nule. To znači da morate sastaviti sve sedmocifrene brojeve telefona od postojećih 10 cifara, a zatim od rezultujućeg broja oduzeti broj brojeva koji počinju sa nulom. Formula će izgledati ovako:
A 10 7 – A 9 6 = 10 9 8 7 6 5 4 – 9 8 7 6 5 4 = 544.320.
Odgovor: 544 320.
Zadatak 4.
Na koliko načina se na polici može složiti 12 knjiga, od kojih su 5 zbirke pjesama, tako da zbirke stoje jedna do druge?
Rješenje.
Prvo, uzmimo 5 zbirki uslovno kao jednu knjigu, jer treba da stoje jedna do druge. Pošto je red u kombinaciji bitan i svi elementi se koriste, to znači da se radi o permutaciji 8 elemenata (7 knjiga + konvencionalna 1 knjiga). Njihov broj je R 8. Zatim ćemo preurediti samo zbirke pjesama među sobom. Ovo se može uraditi na 5 načina. Budući da moramo urediti i zbirke i druge knjige, koristit ćemo pravilo proizvoda. Dakle, P 8 · P 5 = 8! · 5!. Broj načina će biti velik, pa se odgovor može ostaviti u obliku proizvoda faktorijala.
Odgovor: 8! · 5!
Problem 5.
U razredu je 16 dječaka i 12 djevojčica. Za čišćenje prostora u blizini škole potrebna su vam 4 dječaka i 3 djevojčice. Na koliko načina mogu biti odabrani od svih učenika u razredu?
Rješenje.
Prvo, odvojeno biramo 4 dječaka od 16 i 3 djevojčice od 12. Pošto se poredak plasmana ne uzima u obzir, odgovarajuće spojeve su kombinacije bez ponavljanja. S obzirom na potrebu da istovremeno biramo i dječake i djevojčice, koristimo pravilo proizvoda. Kao rezultat toga, broj načina će se izračunati na sljedeći način:
C 16 4 C 12 3 = (16!/(4! 12!)) (12!/(3! 9!)) = ((13 14 15 16) / (2 3 4)) ·((10 · 11) · 12) / (2 · 3)) = 400 400.
Odgovor: 400 400.
Dakle, uspješno rješenje kombinatornog problema zavisi od pravilne analize njegovog stanja, određivanja vrste jedinjenja koja će biti sastavljena i izbora odgovarajuće formule za izračunavanje njihove količine.
Imate još pitanja? Ne znate kako riješiti kombinatorne probleme?
Da biste dobili pomoć od tutora, registrujte se.
Prva lekcija je besplatna!
web stranicu, kada kopirate materijal u cijelosti ili djelomično, link na izvor je obavezan.
Plan:
1. Elementi kombinatorike.
2. Opća pravila kombinatorike.
4. Primjena grafova (šema) u rješavanju kombinatornih zadataka.
1. Kombinatorika i njeno porijeklo.Kombinatorika je oblast matematike u kojoj se proučavaju pitanja o tome koliko se različitih kombinacija, pod određenim uslovima, može napraviti od elemenata koji pripadaju datom skupu.
Kombinatorika je nastala u 16. veku. Kockanje (karte, kockice) zauzimalo je veliko mjesto u životu privilegovanih slojeva društva tog vremena. Lutrije su bile široko rasprostranjene. U početku su se kombinatorni problemi uglavnom odnosili na kockanje: na koliko načina se može dobiti određeni broj poena bacanjem 2 ili 3 kocke, ili na koliko načina se mogu dobiti 2 kralja u određenoj kartaškoj igri. Ovi i drugi problemi kockanja bili su pokretačka snaga u razvoju kombinatorike i daljem razvoju teorije vjerovatnoće.
Jedan od prvih koji je prebrojao broj različitih kombinacija prilikom igranja kockica bio je talijanski matematičar Tartaglia. Sastavio je tabele (broj načina na koji se k poena može pojaviti na r kockicama). Međutim, nije uzeo u obzir da isti broj bodova može pasti na različite načine, pa su njegove tabele sadržavale veliki broj grešaka.
Teorijsko proučavanje kombinatorike su u 17. veku preduzeli francuski matematičari Blez Paskal i Ferma. Polazna tačka njihovog istraživanja bili su i problemi kockanja.
Dalji razvoj kombinatorike vezuje se za imena J. Bernoullija, G. Leibniza, L. Eulera. Međutim, u njihovom radu glavnu ulogu su imale aplikacije za razne igre.
Danas se kombinatorne metode koriste za rješavanje transportnih problema, posebno problema rasporeda, za izradu planova proizvodnje i prodaje proizvoda itd.
2. Opća pravila kombinatorike.Pravilo sume: Ako se neki objekat A može izabrati na m načina, a objekat B na k načina, onda se objekat "ili A ili B" može izabrati na m + k načina.
primjeri:
1. Pretpostavimo da u kutiji ima n loptica različitih boja. 1 lopta se nasumično vadi. Na koliko načina se to može učiniti?
odgovor: n načina.
Podijelimo ovih n loptica u dvije kutije: prva sadrži m loptica, druga sadrži k loptica. 1 loptica je nasumično izvučena iz nasumično odabrane kutije. Na koliko načina se to može učiniti?
Rješenje: Lopta se može izvaditi iz prve kutije na m načina, a iz druge na k načina. Tada je ukupan broj načina m+k=n.
2. Marine semaphore.U pomorskom semaforu svako slovo abecede odgovara određenom položaju dvije zastavice u odnosu na tijelo signalista. Koliko takvih signala može biti?
Rješenje: Ukupan broj je zbir pozicija kada se obje zastavice nalaze na suprotnim stranama tijela signalista i pozicija kada se nalaze na istoj strani tijela signalista. Prilikom brojanja mogućih pozicija primjenjuje se pravilo zbroja.
Pravilo proizvoda: Ako se objekt A može odabrati na m načina, a nakon svakog takvog izbora drugi objekt B može biti odabran (bez obzira na izbor objekta A) na k načina, tada se parovi objekata “A i B” mogu odabrati na m * k načine.
primjeri:
1. Koliko ima dvocifrenih brojeva?Rješenje: Broj desetica se može označiti bilo kojim brojem od 1 do 9. Broj jedinica se može označiti bilo kojim brojem od 0 do 9. Ako je broj desetica 1, tada broj jedinica može biti bilo koji broj (od 0 do 9). Dakle, postoji 10 dvocifrenih brojeva, pri čemu je broj desetica 1. Slično razmišljamo i za bilo koji drugi broj desetica. Tada možemo izračunati da ih ima 9 *10 = 90 dvocifrenih brojeva.
2. Ima 2 fioke. Jedna sadrži m raznobojnih kocki, a druga k raznobojnih loptica. Na koliko načina možete odabrati par “Cube-Ball”?
Rješenje: Izbor lopte ne zavisi od izbora kocke, i obrnuto. Dakle, broj načina na koji se dati par može odabrati je m *k .
3. Populacija bez ponavljanja i uzorak bez ponavljanja.Populacija bez ponavljanja je skup nekog konačnog broja različitih elemenata a 1, a 2, a 3, ..., a n.
primjer: Skup n raznobojni komadići.
Volumen uzorkovanjak (kn) je grupa od m elemenata date populacije.
primjer:Šarena vrpca sašivena od m raznobojnih komadića odabranih iz datog n .
Postings fromn elemenata svakik takvi uzorci se nazivaju oni koji sadrže po k elemenata, odabranih između datih n elemenata opće populacije bez ponavljanja, a razlikuju se jedni od drugih bilo po sastavu elemenata ili po redoslijedu njihovog rasporeda.
- broj plasmana od n od k.
Broj plasmana od n od k može se odrediti na sljedeći način: može se odabrati prvi objekt selekcije n načina, onda se može odabrati drugi objekt n -1 način, itd.
Transformirajući ovu formulu, imamo:
Treba to zapamtiti 0!=1.
primjeri:
1. U prvoj klasi A grupe fudbalskog prvenstva učestvuje 17 ekipa. Dodeljuju se medalje: zlatne, srebrne i bronzane. Na koliko načina se mogu igrati?
Rješenje:Pobjedničke kombinacije timova se međusobno razlikuju po sastavu i redoslijedu elemenata, tj. su plasmani od 17 do 3.
2. Naučno društvo se sastoji od 25 ljudi. Potrebno je izabrati predsjednika društva, potpredsjednika, naučnog sekretara i blagajnika. Na koliko načina se to može učiniti?
Rješenje: Kombinacije menadžmenta preduzeća razlikuju se jedna od druge po sastavu i redosledu elemenata, tj. su plasmani od 25 do 4.
Permutacije bez ponavljanja od nelementinazivaju se položaji bez ponavljanja iz n elemenata od n , tj. položaji se razlikuju jedan od drugog samo po redoslijedu elemenata.
Broj permutacija.
primjeri:
1. Koliko se različitih petocifrenih brojeva može napraviti od cifara 1, 2, 3, 4, 5, pod uslovom da se moraju sastojati od različitih cifara?
Rješenje:Imamo permutacije od 5 elemenata.2. Na koliko načina možete sastaviti 6 raznobojnih komadića u šarenu traku?Rješenje:Imamo permutacije od 6 elemenata.
Kombinacije bez ponavljanja od nelementi pok takvi uzorci se nazivaju oni koji sadrže po k elemenata, odabranih između datih n elemenata opće populacije bez ponavljanja, a razlikuju se jedan od drugog samo po sastavu elemenata.
- broj kombinacija n od k
Elementi svakogmogu se dogovoriti kombinacijenačine. Ondaprimjeri:1. Ako 20 ljudi učestvuje u polufinalu šahovskog prvenstva, a samo troje uđe u finale, na koliko načina se to troje može odrediti?
Rješenje:U ovom slučaju, redosled kojim se ova trojka nalazi nije značajan. Dakle, trojke koje su došle do finala su kombinacije 20 sa 3.
2. Na koliko načina možete odabrati tri delegata od deset ljudi za konferenciju?Rješenje:U ovom slučaju, redosled kojim se ova trojka nalazi nije značajan. Dakle, trojke delegata su kombinacije 10 prema 3.
sažetak:
4. Upotreba grafova (šema) u rješavanju kombinatornih zadataka.
U slučaju kada broj mogućih izbora u svakom koraku zavisi od toga koji su elementi prethodno odabrani, proces sastavljanja kombinacija može se prikazati kao „stablo“. Prvo, onoliko segmenata je izvučeno iz jedne tačke koliko je različitih izbora koji se mogu napraviti u prvom koraku. Sa kraja svakog segmenta nacrtajte onoliko segmenata koliko se može odabrati u drugom koraku, ako je ovaj element odabran u prvom koraku, itd.
zadatak:
Prilikom sastavljanja komandi letjelice uzima se u obzir i pitanje psihološke kompatibilnosti učesnika putovanja. Potrebno je sastaviti posadu svemirskog broda od 3 osobe: komandanta, inženjera i doktora. Za komandirsku poziciju su 4 kandidata: a 1, a 2, a 3, a 4 .Na mjestu inženjera 3:b 1, b 2, b 3. Za mjesto doktora - 3: c 1, c 2, c 3. Pregledom je utvrđeno da je komandira 1 je psihološki kompatibilan sa inženjerima b 1 i b 3 i doktori c 1 i c 3. Komandir a 2 - sa inženjerima b 1 i b 2. i svi doktori. komandantea 3 - sa inženjerimab 1 i b 2 i doktoric 1 i c 3. komandante a 4 - sa svim inženjerima i doktorom c 2 . Pored toga, inženjerb 1 nije kompatibilan sa doktorom c 3, b 2 - kod doktora c 1 i b 3 - kod doktora c 2. Na koliko načina može biti sastavljena posada broda pod ovim uslovima?
Rješenje:
Kreirajmo odgovarajuće "drvo".

odgovor: 10 kombinacija.
Takvo stablo je graf i koristi se za rješavanje kombinatornih problema.
KOMBINATORIKA
Kombinatorika je grana matematike koja proučava probleme odabira i raspoređivanja elemenata iz određenog osnovnog skupa u skladu sa datim pravilima. Formule i principi kombinatorike koriste se u teoriji vjerovatnoće za izračunavanje vjerovatnoće slučajnih događaja i, shodno tome, dobijanje zakona raspodjele slučajnih varijabli. To nam, pak, omogućava proučavanje obrazaca masovnih slučajnih pojava, što je vrlo važno za ispravno razumijevanje statističkih obrazaca koji se manifestiraju u prirodi i tehnologiji.
Pravila za sabiranje i množenje u kombinatorici
Pravilo sume. Ako se dvije radnje A i B međusobno isključuju, a akcija A se može izvesti na m načina, a B na n načina, tada se jedna od ovih radnji (A ili B) može izvesti na n + m načina.
Primjer 1.
U razredu je 16 dječaka i 10 djevojčica. Na koliko načina možete odrediti jednog dežurnog?
Rješenje
Na dužnost mogu biti raspoređeni dječak ili djevojčica, tj. dežurni može biti bilo koji od 16 dječaka ili bilo koja od 10 djevojčica.
Koristeći pravilo zbira, nalazimo da se jedan dežurni može dodijeliti na 16+10=26 načina.
Pravilo proizvoda. Neka postoji k radnji koje je potrebno izvršiti uzastopno. Ako se prva radnja može izvesti na n 1 načina, druga radnja na n 2 načina, treća na n 3 načina, i tako sve do k-te radnje koja se može izvesti na n k načina, tada se svih k radnji mogu izvesti zajedno :
načine.
Primjer 2.
U razredu je 16 dječaka i 10 djevojčica. Na koliko načina se mogu imenovati dva dežurna?
Rješenje
Za prvu dežurnu osobu može biti imenovan dječak ili djevojčica. Jer U odeljenju ima 16 dečaka i 10 devojčica, tada možete postaviti prvu dežurnu na 16+10=26 načina.
Nakon što smo izabrali prvog dežurnog, možemo izabrati drugog od preostalih 25 ljudi, tj. 25 načina.
Prema teoremi množenja, dva pratioca se mogu odabrati na 26*25=650 načina.
Kombinacije bez ponavljanja. Kombinacije sa ponavljanjima
Klasičan problem kombinatorike je problem broja kombinacija bez ponavljanja, čiji se sadržaj može izraziti pitanjem: koliko načine Može izabrati m od n različite stavke?
![]()
Primjer 3.
Morate odabrati 4 od 10 različitih knjiga dostupnih za poklon. Na koliko načina se to može učiniti?
Rješenje
Moramo izabrati 4 knjige od 10, a redosled izbora nije bitan. Dakle, morate pronaći broj kombinacija od 10 elemenata od 4:
![]() .
.
Razmotrimo problem broja kombinacija sa ponavljanjima: postoji r identičnih objekata svakog od n različitih tipova; koliko načine Može izabrati m() od ove (n*r) stavke?
![]() .
.
Primjer 4.
U poslastičarnici su se prodavale 4 vrste kolača: Napoleoni, ekleri, pecivo i lisnato pecivo. Na koliko načina možete kupiti 7 torti?
Rješenje
Jer Među 7 torti mogu biti torte iste vrste, tada je broj načina na koje se može kupiti 7 torti određen brojem kombinacija sa ponavljanjem od 7 do 4.
![]() .
.
Položaji bez ponavljanja. Položaji sa ponavljanjima
Klasičan problem kombinatorike je problem broja postavljanja bez ponavljanja, čiji se sadržaj može izraziti pitanjem: koliko načine Može izabrati I pošta By m drugačiji mjesta m od n drugačije stavke?
![]()
Primjer 5.
Neke novine imaju 12 strana. Na stranicama ovog lista potrebno je postaviti četiri fotografije. Na koliko načina se to može učiniti ako nijedna stranica novina ne smije sadržavati više od jedne fotografije?
Rješenje.
U ovom zadatku ne biramo samo fotografije, već ih postavljamo na određene stranice novina, a svaka stranica novina ne smije sadržavati više od jedne fotografije. Dakle, problem se svodi na klasičan problem određivanja broja plasmana bez ponavljanja 12 elemenata od 4 elementa:
Tako se 4 fotografije na 12 stranica mogu rasporediti na 11.880 načina.
Klasičan problem kombinatorike je i problem broja postavljanja sa ponavljanjima, čiji se sadržaj može izraziti pitanjem: koliko načine Može Vibarmije I pošta By m drugačiji mjesta m od n stavki,Withspreman koji Tu je isto?
Primjer 6.
Dječak je još uvijek imao markice sa brojevima 1, 3 i 7 iz svog seta društvenih igara. Odlučio je da pomoću ovih markica stavi petocifreni brojevi na sve knjige kako bi napravio katalog. Koliko različitih petocifrenih brojeva može stvoriti dječak?
Permutacije bez ponavljanja. Permutacije s ponavljanjima
Klasičan problem kombinatorike je problem broja permutacija bez ponavljanja, čiji se sadržaj može izraziti pitanjem: koliko načine Može pošta n razne stavke on n drugačije mjesta?
Primjer 7.
Koliko "reči" od četiri slova možete napraviti od slova reči "brak"?
Rješenje
Opšta populacija je 4 slova riječi “brak” (b, p, a, k). Broj "riječi" određen je permutacijama ova 4 slova, tj.
![]()
Za slučaj kada među odabranih n elemenata ima identičnih (izbor sa povratkom), problem broja permutacija sa ponavljanjima može se izraziti pitanjem: Na koliko načina se n objekata koji se nalaze na n različitih mjesta mogu preurediti ako među n objekata postoji k različitih tipova (k< n), т. е. есть одинаковые предметы.

Primjer 8.
Koliko se različitih kombinacija slova može napraviti od slova riječi "Mississippi"?
Rješenje
Postoji 1 slovo "m", 4 slova "i", 3 slova "c" i 1 slovo "p", ukupno 9 slova. Dakle, broj permutacija sa ponavljanjima je jednak
![]()
SAŽETAK ZA SEKCIJU "KOMBINATORIKA"
Kombinatorika je grana matematike koja proučava pitanja o tome koliko se različitih kombinacija, pod određenim uvjetima, može napraviti od datih objekata. Osnove kombinatorike su veoma važne za procenu verovatnoće slučajnih događaja, jer Oni nam omogućavaju da izračunamo suštinski mogući broj različitih opcija za razvoj događaja.
Osnovna formula kombinatorike
Neka postoji k grupa elemenata, a i-ta grupa se sastoji od n i elemenata. Odaberimo po jedan element iz svake grupe. Tada je ukupan broj N načina na koje se takav izbor može napraviti određen relacijom N=n 1 *n 2 *n 3 *...*n k .
Primjer 1. Objasnimo ovo pravilo jednostavnim primjerom. Neka postoje dvije grupe elemenata, i prva grupa se sastoji od n 1 elemenata, a druga - od n 2 elementa. Koliko se različitih parova elemenata može napraviti od ove dvije grupe, tako da par sadrži po jedan element iz svake grupe? Recimo da smo uzeli prvi element iz prve grupe i, ne menjajući ga, prošli sve moguće parove, menjajući samo elemente iz druge grupe. Za ovaj element može postojati n 2 takva para. Zatim uzimamo drugi element iz prve grupe i također pravimo sve moguće parove za njega. Također će biti n 2 takva para. Pošto postoji samo n 1 elemenata u prvoj grupi, ukupne moguće opcije će biti n 1 *n 2 .
Primjer 2. Koliko se trocifrenih parnih brojeva može sastaviti od cifara 0, 1, 2, 3, 4, 5, 6, ako se cifre mogu ponavljati?
Rješenje: n 1 =6 (jer možete uzeti bilo koji broj od 1, 2, 3, 4, 5, 6 kao prvu cifru), n 2 =7 (jer možete uzeti bilo koji broj od 0 kao drugu cifru, 1, 2 , 3, 4, 5, 6), n 3 =4 (pošto se bilo koji broj od 0, 2, 4, 6 može uzeti kao treća cifra).
Dakle, N=n 1 *n 2 *n 3 =6*7*4=168.
U slučaju kada se sve grupe sastoje od istog broja elemenata, tj. n 1 =n 2 =...n k =n možemo pretpostaviti da je svaka selekcija napravljena iz iste grupe, a element nakon selekcije se vraća u grupu. Tada je broj svih metoda selekcije n k . Ova metoda selekcije u kombinatorici se zove uzorci sa povratom.
Primjer 3. Koliko se četvorocifrenih brojeva može sastaviti od cifara 1, 5, 6, 7, 8?
Rješenje. Za svaku cifru četvorocifrenog broja postoji pet mogućnosti, što znači N=5*5*5*5=5 4 =625.
Razmotrimo skup koji se sastoji od n elemenata. U kombinatorici se ovaj skup naziva opšta populacija.
Broj postavljanja n elemenata po m
Definicija 1. Smještaj od n elementi po m u kombinatorici bilo naručeni set od m različiti elementi odabrani iz populacije u n elementi.
Primjer 4. Različiti rasporedi tri elementa (1, 2, 3) po dva bit će skupovi (1, 2), (2, 1), (1, 3), (3, 1), (2, 3), (3 , 2 ). Položaji se mogu međusobno razlikovati i po elementima i po njihovom redoslijedu.
Broj plasmana u kombinatorici označava se sa A n m i izračunava se po formuli:
komentar: n!=1*2*3*...*n (čitaj: “en factorial”), osim toga, pretpostavlja se da je 0!=1.
Primjer 5. Koliko ima dvocifrenih brojeva u kojima su cifra desetice i cifra jedinice različite i neparne?
Rješenje: jer Ako postoji pet neparnih cifara, odnosno 1, 3, 5, 7, 9, onda se ovaj zadatak svodi na odabir i postavljanje dvije od pet različitih cifara na dvije različite pozicije, tj. naznačeni brojevi će biti:
Definicija 2. Kombinacija od n elementi po m u kombinatorici bilo neuređen skup od m različiti elementi odabrani iz populacije u n elementi.
Primjer 6. Za skup (1, 2, 3), kombinacije su (1, 2), (1, 3), (2, 3).
Broj kombinacija od n elemenata, po m
Broj kombinacija je označen sa C n m i izračunava se po formuli:
![]()
Primjer 7. Na koliko načina čitalac može izabrati dvije knjige od šest dostupnih?
Rješenje: Broj metoda jednak je broju kombinacija šest knjiga od dvije, tj. jednako:
![]()
Permutacije n elemenata
Definicija 3. Permutacija od n elementi se nazivaju bilo koji naručeni set ovih elemenata.
Primjer 7a. Sve moguće permutacije skupa koji se sastoji od tri elementa (1, 2, 3) su: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3) , ( 3, 2, 1), (3, 1, 2).
Broj različitih permutacija n elemenata označava se sa P n i izračunava se formulom P n =n!.
Primjer 8. Na koliko načina se sedam knjiga različitih autora može poredati u jedan red na polici?
Rješenje: Ovaj problem se odnosi na broj permutacija sedam različitih knjiga. Postoji P 7 =7!=1*2*3*4*5*6*7=5040 načina da uredite knjige.
Diskusija. Vidimo da se broj mogućih kombinacija može izračunati prema različitim pravilima (permutacije, kombinacije, plasmani) i rezultat će biti drugačiji, jer Princip izračuna i same formule su različiti. Gledajući pažljivo definicije, primijetit ćete da rezultat ovisi o nekoliko faktora istovremeno.
Prvo, od toga koliko elemenata možemo kombinirati njihove skupove (koliko je velik ukupnost elemenata).
Drugo, rezultat ovisi o veličini skupova elemenata koji su nam potrebni.
Konačno, važno je znati da li je redoslijed elemenata u skupu značajan za nas. Objasnimo posljednji faktor koristeći sljedeći primjer.
Primjer 9. Na roditeljskom sastanku je prisutno 20 osoba. Koliko različitih opcija postoji za sastav roditeljskog odbora ako mora da ima 5 ljudi?
Rješenje: U ovom primeru nas ne zanima redosled imena na listi odbora. Ako se kao rezultat toga ispostavi da su isti ljudi dio toga, onda je u smislu za nas ovo ista opcija. Stoga možemo koristiti formulu za izračunavanje broja kombinacije od 20 elemenata po 5.
Stvari će biti drugačije ako je svaki član komisije u početku odgovoran za određeno područje rada. Zatim, sa istim spiskovim sastavom komisije, u njoj je moguće 5! opcije permutacije to je bitno. Broj različitih (i po sastavu i po području odgovornosti) opcija određen je u ovom slučaju brojem plasmani od 20 elemenata po 5.
Zadaci za samotestiranje
1. Koliko se trocifrenih parnih brojeva može sastaviti od cifara 0, 1, 2, 3, 4, 5, 6, ako se cifre mogu ponavljati?
2. Koliko ima petocifrenih brojeva koji se čitaju isto s lijeva na desno i s desna na lijevo?
3. U razredu ima deset predmeta i pet časova dnevno. Na koliko načina možete kreirati raspored za jedan dan?
4. Na koliko načina mogu biti izabrana 4 delegata za konferenciju ako ima 20 ljudi u grupi?
5. Na koliko načina se osam različitih pisama može staviti u osam različitih koverti, ako se u svaku kovertu stavi samo jedno slovo?
6. Komisija koju čine dva matematičara i šest ekonomista treba da budu sastavljena od tri matematičara i deset ekonomista. Na koliko načina se to može učiniti?